2022-2023 数学鲁教版新中考精讲精练 考点09 一次函数

这是一份2022-2023 数学鲁教版新中考精讲精练 考点09 一次函数，文件包含2022-2023数学鲁教版新中考精讲精练考点09一次函数原卷版docx、2022-2023数学鲁教版新中考精讲精练考点09一次函数解析版docx等2份试卷配套教学资源，其中试卷共36页， 欢迎下载使用。

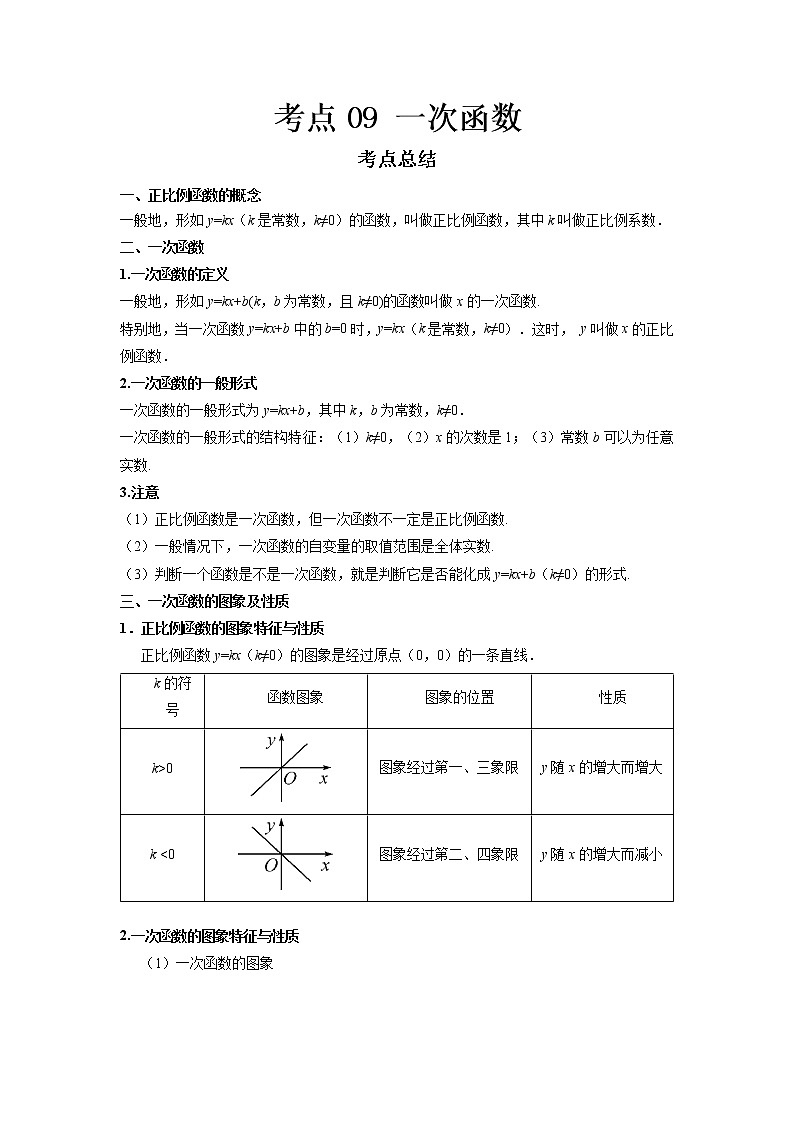
考点09 一次函数
考点总结
一、正比例函数的概念
一般地，形如y=kx（k是常数，k≠0）的函数，叫做正比例函数，其中k叫做正比例系数．
二、一次函数
1.一次函数的定义
一般地，形如y=kx+b(k，b为常数，且k≠0)的函数叫做x的一次函数.
特别地，当一次函数y=kx+b中的b=0时，y=kx（k是常数，k≠0）．这时， y叫做x的正比例函数．
2.一次函数的一般形式
一次函数的一般形式为y=kx+b，其中k，b为常数，k≠0．
一次函数的一般形式的结构特征：（1）k≠0，（2）x的次数是1；（3）常数b可以为任意实数.
3.注意
（1）正比例函数是一次函数，但一次函数不一定是正比例函数.
（2）一般情况下，一次函数的自变量的取值范围是全体实数.
（3）判断一个函数是不是一次函数，就是判断它是否能化成y=kx+b（k≠0）的形式.
三、一次函数的图象及性质
1．正比例函数的图象特征与性质
正比例函数y=kx（k≠0）的图象是经过原点（0，0）的一条直线．
k的符号
函数图象
图象的位置
性质
k>0

图象经过第一、三象限
y随x的增大而增大
k <0

图象经过第二、四象限
y随x的增大而减小

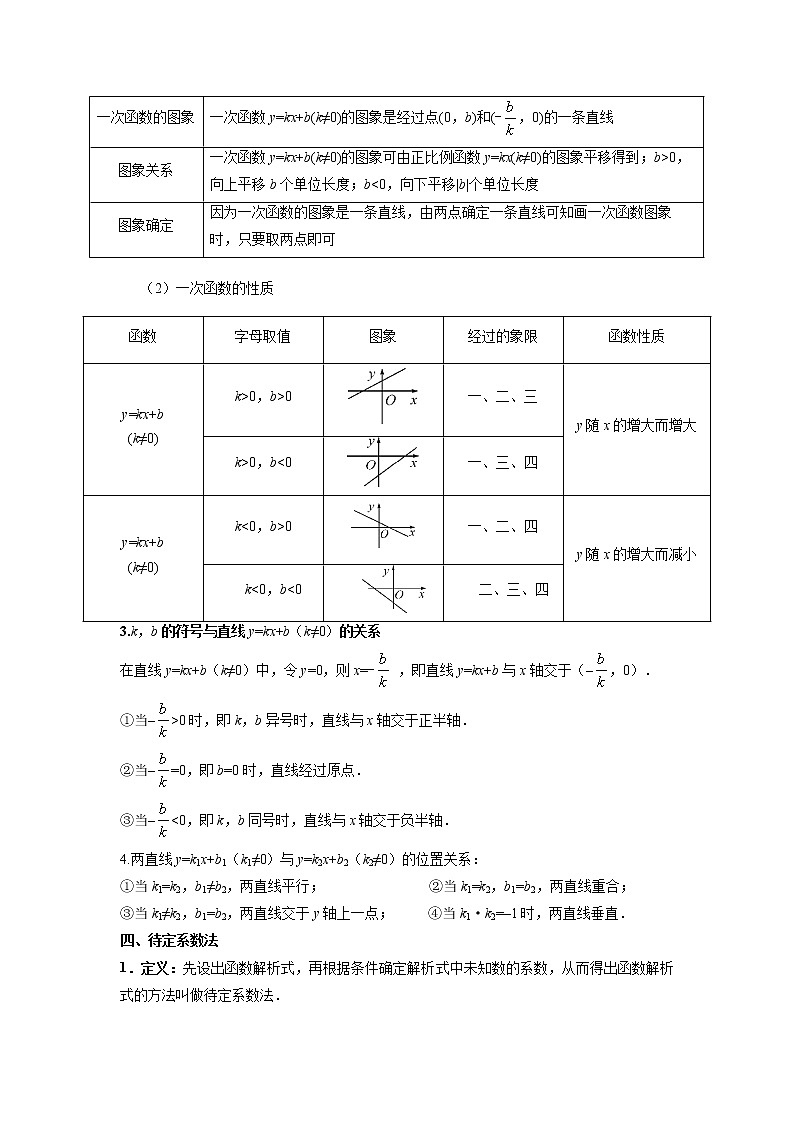
2.一次函数的图象特征与性质
（1）一次函数的图象
一次函数的图象
一次函数y=kx+b(k≠0)的图象是经过点(0，b)和(-，0)的一条直线
图象关系
一次函数y=kx+b(k≠0)的图象可由正比例函数y=kx(k≠0)的图象平移得到；b>0，向上平移b个单位长度；b<0，向下平移|b|个单位长度
图象确定
因为一次函数的图象是一条直线，由两点确定一条直线可知画一次函数图象时，只要取两点即可
（2）一次函数的性质
函数
字母取值
图象
经过的象限
函数性质
y=kx+b
(k≠0)
k>0，b>0

一、二、三
y随x的增大而增大
k>0，b<0

一、三、四
y=kx+b
(k≠0)
k<0，b>0

一、二、四
y随x的增大而减小
k<0，b<0

二、三、四
3.k，b的符号与直线y=kx+b（k≠0）的关系
在直线y=kx+b（k≠0）中，令y=0，则x=- ，即直线y=kx+b与x轴交于（–，0）．
①当–>0时，即k，b异号时，直线与x轴交于正半轴．
②当–=0，即b=0时，直线经过原点．
③当–<0，即k，b同号时，直线与x轴交于负半轴．
4.两直线y=k1x+b1（k1≠0）与y=k2x+b2（k2≠0）的位置关系：
①当k1=k2，b1≠b2，两直线平行； ②当k1=k2，b1=b2，两直线重合；
③当k1≠k2，b1=b2，两直线交于y轴上一点； ④当k1·k2=–1时，两直线垂直．
四、待定系数法
1．定义：先设出函数解析式，再根据条件确定解析式中未知数的系数，从而得出函数解析式的方法叫做待定系数法．
2．待定系数法求正比例函数解析式的一般步骤
（1）设含有待定系数的函数解析式为y=kx（k≠0）．
（2）把已知条件（自变量与函数的对应值）代入解析式，得到关于系数k的一元一次方程．
（3）解方程，求出待定系数k．
（4）将求得的待定系数k的值代入解析式．
3．待定系数法求一次函数解析式的一般步骤
（1）设出含有待定系数k、b的函数解析式y=kx+b．
（2）把两个已知条件（自变量与函数的对应值）代入解析式，得到关于系数k，b的二元一次方程组．
（3）解二元一次方程组，求出k，b．
（4）将求得的k，b的值代入解析式．
五、一次函数与正比例函数的区别与联系


正比例函数
一次函数
区别
一般形式
y=kx+b（k是常数，且k≠0）
y=kx+b（k，b是常数，且k≠0）
图象
经过原点的一条直线
一条直线
k，b符号的作用
k的符号决定其增减性，同时决定直线所经过的象限
k的符号决定其增减性；b的符号决定直线与y轴的交点位置；k，b的符号共同决定直线经过的象限
求解析式的条件
只需要一对x，y的对应值或一个点的坐标
需要两对x，y的对应值或两个点的坐标
联系
比例函数是特殊的一次函数．
②正比例函数图象与一次函数图象的画法一样，都是过两点画直线，但画一次函数的图象需取两个不同的点，而画正比例函数的图象只要取一个不同于原点的点即可．
③一次函数y=kx+b（k≠0）的图象可以看作是正比例函数y=kx（k≠0）的图象沿y轴向上（b>0）或向下（b<0）平移|b|个单位长度得到的．由此可知直线y=kx+b（k≠0，b≠0）与直线y=kx（k≠0）平行．
④一次函数与正比例函数有着共同的性质：
a．当k>0时，y的值随x值的增大而增大；b．当k<0时，y的值随x值的增大而减小．
六、一次函数与方程（组）、不等式
1．一次函数与一元一次方程
任何一个一元一次方程都可以转化为kx+b=0(k，b为常数，且k≠0)的形式．
从函数的角度来看，解这个方程就是寻求自变量为何值时函数值为0；从函数图象的角度考虑，解这个方程就是确定直线y=kx+b与x轴的交点的横坐标．
2．一次函数与一元一次不等式
任何一个一元一次不等式都能写成ax+b>0（或ax+b<0）（a，b为常数，且a≠0）的形式．
从函数的角度看，解一元一次不等式就是寻求使一次函数y=ax+b（a≠0）的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=ax+b（a≠0）在x轴上（或下）方部分的点的横坐标满足的条件．
3．一次函数与二元一次方程组
一般地，二元一次方程mx+ny=p（m，n，p是常数，且m≠0，n≠0）都能写成y=ax+b（a，b为常数，且a≠0）的形式．因此，一个二元一次方程对应一个一次函数，又因为一个一次函数对应一条直线，所以一个二元一次方程也对应一条直线．进一步可知，一个二元一次方程对应两个一次函数，因而也对应两条直线．
从数的角度看，解二元一次方程组相当于考虑自变量为何值时，两个函数的值相等，以及这两个函数值是何值；从形的角度看，解二元一次方程组相当于确定两条直线的交点坐标，一般地，如果一个二元一次方程组有唯一解，那么这个解就是方程组对应的两条直线的交点坐标．
七、一次函数图象与图形面积
解决这类问题的关键是根据一次函数解析式求出一次函数图象与坐标轴的交点的坐标，或两条直线的交点坐标，进而将点的坐标转化成三角形的边长，或者三角形的高．如果围成的三角形没有边在坐标轴上或者与坐标轴平行，可以采用“割”或“补”的方法．
八、一次函数的实际应用
1．主要题型： （1）求相应的一次函数表达式；（2）结合一次函数图象求相关量、求实际问题的最值等．
2．用一次函数解决实际问题的一般步骤为：
（1）设定实际问题中的自变量与因变量；（2）通过列方程(组)与待定系数法求一次函数关系式；（3）确定自变量的取值范围；（4）利用函数性质解决问题；（5）检验所求解是否符合实际意义；（6）答．
3．方案最值问题：
对于求方案问题，通常涉及两个相关量，解题方法为根据题中所要满足的关系式，通过列不等式，求解出某一个事物的取值范围，再根据另一个事物所要满足的条件，即可确定出有多少种方案．
4．方法技巧
求最值的本质为求最优方案，解法有两种：（1）可将所有求得的方案的值计算出来，再进行比较；
（2）直接利用所求值与其变量之间满足的一次函数关系式求解，由一次函数的增减性可直接确定最优方案及最值；若为分段函数，则应分类讨论，先计算出每个分段函数的取值，再进行比较．
显然，第（2）种方法更简单快捷．
真题演练
一．选择题（共10小题）
1．（2021•高唐县一模）若一次函数y＝x+m与y＝﹣x+3的图象交点在第一象限，则m的取值范围是（　　）
A．﹣9＜m＜3 B．0＜m＜3 C．m＜0或m＞3 D．m＜﹣9或m＞3
【分析】利用两直线相交的问题，通过解方程组得两直线的交点坐标，再利用第一象限点的坐标特征得到不等式组，即可求出m的取值范围．
【解答】解：由题意可得：
，
解得：，
∵交点在第一象限，
∴，
解得：﹣9＜m＜3，
故选：A．
2．（2021•章丘区模拟）如图，在平面直角坐标系中，动点A、B分别在x轴负半轴上和函数y＝x的图象上，AB＝4，CB⊥AB，BC＝2，则OC的最大值为（　　）

A． B． C． D．
【分析】连接AC，根据勾股定理可计算出AC的长，当点A与点O重合时即OC最长，等于AC的长度，即可得出答案．
【解答】解：连接AC交y轴于点E，如图，

在Rt△ABC中，
AC＝，
则在△AOC中，
∠AOC＝∠AOE+∠EOC＝90°+∠EOC≥90°，
故∠CAO＜90°，
则 OC≤CA，
∴当且仅当点A与点O重合时，OC为最大值，
OC＝AC＝2，
故选：C．
3．（2021•德城区二模）若以关于x、y的二元一次方程x+2y﹣b＝0的解为坐标的点（x，y）都在直线y＝﹣x+b﹣1上，则常数b的值为（　　）
A． B．1 C．﹣1 D．2
【分析】直线解析式乘以2后和方程联立解答即可．
【解答】解：因为以关于x、y的二元一次方程x+2y﹣b＝0的解为坐标的点（x，y）都在直线y＝﹣x+b﹣1上，
直线解析式乘以2得2y＝﹣x+2b﹣2，变形为：x+2y﹣2b+2＝0，
所以b﹣2b+2＝0，
解得：b＝2，
故选：D．
4．（2021•商河县二模）已知，直线y＝（m﹣2）x+n经过第二、三、四象限，则m的取值范围在数轴上表示为（　　）
A． B．
C． D．
【分析】由直线经过第二、三、四象限，可得出m﹣2＜0，解之可得出m＜2，再对照四个选项即可得出结论．
【解答】解：∵直线y＝（m﹣2）x+n经过第二、三、四象限，
∴m﹣2＜0，n＜0，
∴m＜2．
故选：C．
5．（2021•环翠区模拟）若把一次函数y＝kx+b的图象先绕着原点旋转180°，再向右平移2个单位长度后，恰好经过点A（4，0）和点B（0，﹣2），则原一次函数的表达式为（　　）
A．y＝﹣x﹣1 B．y＝﹣x+1 C．y＝x+1 D．y＝x﹣1
【分析】先利用待定系数法求出直线AB的解析式，再求出将直线AB向左平移2个单位长度后得到的解析式，然后将所得解析式绕着原点旋转180°即可得到原一次函数的表达式．
【解答】解：设直线AB的解析式为y＝mx+n．
∵A（4，0），B（0，﹣2），
∴，
解得，
∴直线AB的解析式为y＝x﹣2．
将直线AB向左平移2个单位长度后得到的解析式为y＝（x+2）﹣2，即y＝x﹣1，
再将y＝x﹣1绕着原点旋转180°后得到的解析式为y＝x+1，
所以原一次函数的表达式是y＝x+1．
故选：C．
6．（2021•招远市一模）有下列四个函数：①y＝2x②y＝﹣x③y＝④y＝﹣（x﹣）2+，其中图象经过如图所示的阴影部分（包括边界）的函数有（　　）

A．1 个 B．2个 C．3 个 D．4个
【分析】根据题目中的函数解析式和性质，可以判断是否符合题意，从而可以解答本题．
【解答】解：在函数y＝2x中，当x＝1时，y＝2，故①符合题意；
函数y＝﹣x的图象经过二、四象限，故②不符合题意；
函数y＝经过一、三象限，当x＝2时，y＝2，故③符合题意；
函数y＝﹣（x﹣）2+的图象开口向下，对称轴是直线x＝当x＝1时，y＝＞3，当x＝2时，y＝＞3，故④不符合题意；
故选：B．
7．（2021•沂县二模）如图，直线y＝kx+b经过点A（﹣1，m）和点B（﹣2，0），直线y＝2x过点A，则不等式2x＜kx+b的解集为（　　）

A．x＜﹣1 B．x＜﹣2 C．x＞﹣1 D．x＞﹣2
【分析】不等式2x＜kx+b的解集，就是指直线y＝2x落在直线y＝k+b的下方的自变量的取值范围．
【解答】解：观察图象可知，当x＜﹣1时，直线y＝2x落在直线y＝k+b的下方，
∴不等式2x＜kx+b解集为x＜﹣1，
故选：A．
8．（2021•历城区模拟）如图，直线y＝kx+b（k＜0）经过点P（1，1），当kx+b≤x，则x的取值范围是（　　）

A．x≥1 B．x＞1 C．x≤1 D．x＜1
【分析】点P（1，1）是直线y＝kx+b（k＜0）与直线y＝x的交点，根据图象即可求得．
【解答】解：直线y＝kx+b（k＜0）经过点P（1，1），直线y＝x也经过点P（1，1），
由图象可知，当x≥1时，直线y＝kx+b（k＜0）不在直线y＝x的上方，
∴当kx+b≤x，则x的取值范围是x≥1；
故选：A．

9．（2021•槐荫区一模）若直线l1经过点（0，3），直线l2经过点（5，2），且l1与l2关于x轴对称，则l1与l2的交点坐标为（　　）
A．（﹣2，0） B．（2，0） C．（﹣3，0） D．（3，0）
【分析】根据对称的性质得出点（0，3）关于x轴对称的对称点，再根据待定系数法确定直线l2的关系式，求出直线l2与x轴的交点即可．
【解答】解：设直线l2的解析式为y＝kx+b，
∵直线l1经过点（0，3），l2经过点（5，2），且l1与l2关于x轴对称，
∴两直线相交于x轴上，点（0，3）关于x轴的对称点（0，﹣3）在直线l2上，
把（0，﹣3）和（5，2）代入y＝kx+b，得，
解得：，
故直线l2的解析式为：y＝x﹣3，
令y＝0，则x＝3，
即l1与l2的交点坐标为（3，0）．
故选：D．
10．（2021•商河县校级模拟）已知直线l1：y＝﹣3x+b与直线l2：y＝﹣kx+m在同一平面直角坐标系中交于点（1，﹣2），那么方程组的解是（　　）
A． B． C． D．
【分析】根据两个一次函数组成的方程组的解就是两函数图象的交点可得答案．
【解答】解：∵直线l1：y＝﹣3x+b与直线l2：y＝﹣kx+m在同一坐标系中的图象交于点（1，﹣2），
∴方程组的解是，
故选：A．
二．填空题（共5小题）
11．（2021•沂水县一模）定义：若两个函数的图象关于直线y＝x对称，则称这两个函数互为反函数．请写出函数y＝﹣2x+1的反函数的解析式 　y＝　．
【分析】求出函数和x轴、y轴的交点坐标，求出对称的点的坐标，再代入函数解析式求出即可．
【解答】解：在y＝﹣2x+1中，
当x＝0时，y＝1，
当y＝0时，x＝，
即函数和x轴的交点为（，0），和y轴的交点坐标为（0，1），
所以两点关于直线y＝x对称的点的坐标分别为（0，）和（1，0），
设函数y＝﹣2x+1的反函数的解析式为y＝kx+b，
把（0，）和（1，0）代入，可得：
，
解得：，
∴函数y＝﹣2x+1的反函数的解析式为y＝﹣x+，
故答案为：y＝﹣x+．
12．（2021•广饶县二模）如图，在平面直角坐标系xOy中，菱形OABC满足点O在原点，点A坐标为（2，0），∠AOC＝60°，直线y＝﹣3x+b与菱形OABC有交点，则b的取值范围为 　　．

【分析】作CM⊥OA于点M，BN⊥OA于点N，求出B的坐标，然后代入一次函数解析式中，求出b的最大值，再将原点代入一次函数解析式中求出b的最小值即可．
【解答】解：作CM⊥OA于点M，BN⊥OA于点N，

∵∠AOC＝60°，∠CMO＝90°，
∴，
∵在菱形OABC中，A（2，0），
∴OC＝OA＝2＝CB，
∴OM＝1，
∴，
∴，
∴B的横坐标为3，
∵OA∥CB，
∴BN＝CM＝，
∴B的纵坐标也为，即，
当y＝﹣3x+b过O（0，0）时，b最小，最小值为0，
当y＝﹣3x+b过时，b最大，
把代入y＝﹣3x+b，
解得：，
∴b的取值范围为：，
故答案为：．
13．（2021•任城区校级一模）已知一次函数y＝kx+3的图象不经过第三象限，若点（2，y1）和（﹣1，y2）均在函数图象上，那么y1与y2的大小关系为 　y1＜y2　．
【分析】由一次函数y＝kx+3的图象不经过第三象限，利用一次函数图象与系数的关系可得出k＜0，利用一次函数的性质可得出y随x的增大而减小，结合2＞﹣1，即可得出y1＜y2．
【解答】解：∵一次函数y＝kx+3的图象不经过第三象限，即一次函数y＝kx+3的图象经过第一、二、四象限，
∴k＜0，
∴y随x的增大而减小．
又∵点（2，y1）和（﹣1，y2）均在函数图象上，2＞﹣1，
∴y1＜y2．
故答案为：y1＜y2．
14．（2021•广饶县一模）如图，在平面直角坐标系中，函数y＝2x和y＝﹣x的图象分别为直线l1、l2，点（1，0）作x轴的垂线交l1于点A1，过点A1作y轴的垂线交l2于点A2，过点A2作x轴的垂线交l1于点A3，过点A3作y轴的垂线交l2于点A4，…依次进行下去．则点A2021的横坐标为 　21010　．

【分析】把点（1，0）代入y＝2x求出A1坐标，进而求得A2、A3坐标，可得A4、A6坐标，据此找到规律，即可得A2021坐标．
【解答】解：∵过点（1，0）作x轴的垂线交l1于点A1，
∴A1（1，2），
把y＝2代入y＝﹣x得x＝﹣2，即A2（﹣2，2），
把x＝﹣2代入y＝2x得y＝﹣4，即A3（﹣2，﹣4），
同理可得A4（4，﹣4），A5（4，8），
∴A2n+1（（﹣2）n，2×（﹣2）n）（n为自然数），
∵2021＝1010×2+1，
∴A2021的坐标为（（﹣2）1010，2×（﹣2）1010）＝（21010，21011）．
∴点A2021的横坐标为21010，
故答案为：21010．
15．（2021•德州）小亮从学校步行回家，图中的折线反映了小亮离家的距离S（米）与时间t（分钟）的函数关系，根据图象提供的信息，给出以下结论：①他在前12分钟的平均速度是70米/分钟；②他在第19分钟到家；③他在第15分钟离家的距离和第24分钟离家的距离相等；④他在第33分钟离家的距离是720米．其中正确的序号为 　①④　．

【分析】由图象可以直接得出前12分钟小亮的平均速度，从而得出①正确；由图象可知从12分到19分小亮又返回学校，可以判断②错误；分别求出小亮第15分和第24分离家距离可以判断③错误；求出小亮33分离家距离，可以判断④正确．
【解答】解：由图象知，前12分中的平均速度为：（1800﹣960）÷12＝70（米/分），
故①正确；
由图象知，小亮第19分中又返回学校，
故②错误；
小亮在返回学校时的速度为：（1800﹣960）÷（19﹣12）＝840÷7＝120（米/分），
∴第15分离家距离：960+（15﹣12）×120＝1320，
从21分到41分小亮的速度为：1800÷（41﹣21）＝1800÷20＝90（米/分），
∴第24分离家距离：1800﹣（24﹣21）×90＝1800﹣270＝1530（米），
∵1320≠1530，
故③错误；
小亮在33分离家距离：1800﹣（33﹣21）×90＝1800﹣1080＝720（米），
故④正确，
故答案为：①④．
三．解答题（共3小题）
16．（2021•胶州市校级模拟）在一条笔直的公路旁依次有A、B、C三个村庄，甲、乙两人同时分别从A、B两村出发，甲骑摩托车，乙骑电动车沿公路匀速驶向C村，最终到达C村．设甲、乙两人到C村的距离y1，y2（km）与行驶时间x（h）之间的函数关系如图所示，请回答下列问题．
（1）A，C两村间的距离为 　120　km，a＝　2　．
（2）求出图中点P的坐标，并解释该点坐标所表示的实际意义．
（3）乙在行驶过程中，何时距甲20km．

【分析】（1）由图可知与y轴交点的坐标表示A、C两村间的距离为120km，再由0.5小时距离C村90km，行驶120﹣90＝30km，速度为60km/h，求得a＝2；
（2）利用待定系数法求出y2的关系式，令y1＝y2，解方程得出点P横坐标，再求纵坐标，由题意及图象可知，在点P处甲乙二人相遇，问题即可解决；
（3）由（2）中的函数解析式根据距甲20km建立方程；探讨得出答案即可．
【解答】解：（1）A、C两村间的距离120km，
a＝120÷[（120﹣90）÷0.5]＝2；
故答案为120，2；
（2）设y2＝k2x+90，
代入（3，0），得0＝3k2+90，
解得k2＝﹣30，
所以y2＝﹣30x+90．
当y1＝y2时，
﹣60t+120＝﹣30t+90，
解得：t＝1，
所以甲乙二人行驶1小时后两人相遇，
此时距离C村60km，
故P点坐标为P（1，60）．
（3）当y1﹣y2＝20，
即﹣60x+120﹣（﹣30x+90）＝20
解得x＝，
当y2﹣y1＝20，
即﹣30x+90﹣（﹣60x+120）＝20
解得x＝，
当甲走到C地，而乙距离C地20km时，
﹣30x+90＝20
解得x＝；
综上所知当x＝h，或x＝h，或x＝h乙距甲20km．
17．（2021•胶州市一模）某文具店店主到批发中心选购甲、乙两种品牌的文具盒，预计购进乙品牌文具盒的数量y（个）与甲品牌文具盒的数量x（个）之间的函数关系如图所示．
（1）求y与x之间的函数关系式；
（2）该店主用3000元选购了甲品牌的文具盒，又用同样的钱选购了乙品牌的文具盒．已知甲品牌文具盒的单价是乙品牌单价的1.5倍，求所选购的甲、乙文具盒的数量．

【分析】（1）根据函数图象中的数据，可以计算出y与x之间的函数关系式；
（2）根据题意和（1）中的函数关系式，可以计算出所选购的甲、乙文具盒的数量．
【解答】解：（1）设y与x的函数关系式为y＝kx+b，
∵点（50，250），（200，100）在该函数图象上，
∴，
解得，
即y与x的函数关系式为y＝﹣x+300；
（2）设乙种文具盒的单价为a元，则甲种文具盒的单价为1.5a元，
则x＝＝，y＝，
∴+300，
解得a＝，
经检验，a＝是原分式方程的解，
∴x＝＝120，y＝＝180，
答：所选购的甲种文具盒120个、乙种文具盒180个．
18．（2021•青岛模拟）端午节是中国首个入选世界非遗的节日，日期是每年农历五月初五．民间有“赛龙舟“、“吃粽子”等习俗．某超市用400元购进甲种粽子礼盒若干盒，用780元购进乙种粽子礼盒若干盒，进行节日前试销，所购乙种礼盒比甲种礼盒多10盒，且乙种每盒进价是甲种每盒进价的1.3倍．
（1）甲，乙两种粽子礼盒每盒进价分别为多少元？
（2）如果购进甲，乙两种粽子共550盒，甲种礼盒购进不多于350盒，为了使总费用最低，应购进甲种礼盒和乙种礼盒各多少盒？总费用最低是多少元？
【分析】（1）设甲种粽子礼盒每盒进价为x元，则乙种粽子礼盒每盒进价为1.3x元，根据用780元所购乙种粽子礼盒比用400元购进甲种粽子礼盒多10盒列出方程，解方程即可，注意验根；
（2）根据总费用等于甲乙礼盒费用之和列出函数关系式，并根据函数的性质和甲种礼盒购进不多于350盒求最值即可．
【解答】解：（1）设甲种粽子礼盒每盒进价为x元，则乙种粽子礼盒每盒进价为1.3x元，
由题意，得，
解得x＝20，
经检验x＝20是原方程的解，
20×1.3＝26元，
答：甲种粽子礼盒每盒进价为20元，则乙种粽子礼盒每盒进价为26元；
（2）由（1）可知甲种粽子礼盒每盒进价为20元，则乙种粽子礼盒每盒进价为26元，
设购进甲种粽子礼盒t盒，总费用为w元，
则，w＝20t+26×（550﹣t）
＝﹣6t+14300
∵w是一次函数，k＝﹣6＜0，
∴w随着t的增大而减小．
又因为t≤350，
∴当t＝350时，w最小，
此时乙种粽子礼盒有：550﹣350＝200盒，
∴w＝﹣6×350+14300＝12200（元），
答：购进甲种粽子礼盒350盒，乙种粽子礼盒200盒最低费用为12200元．