2022-2023学年黑龙江省双鸭山市饶河县高级中学高一上学期期中数学试题（解析版）

2022-2023学年黑龙江省双鸭山市饶河县饶河县高级中学高一上学期期中数学试题

一、单选题

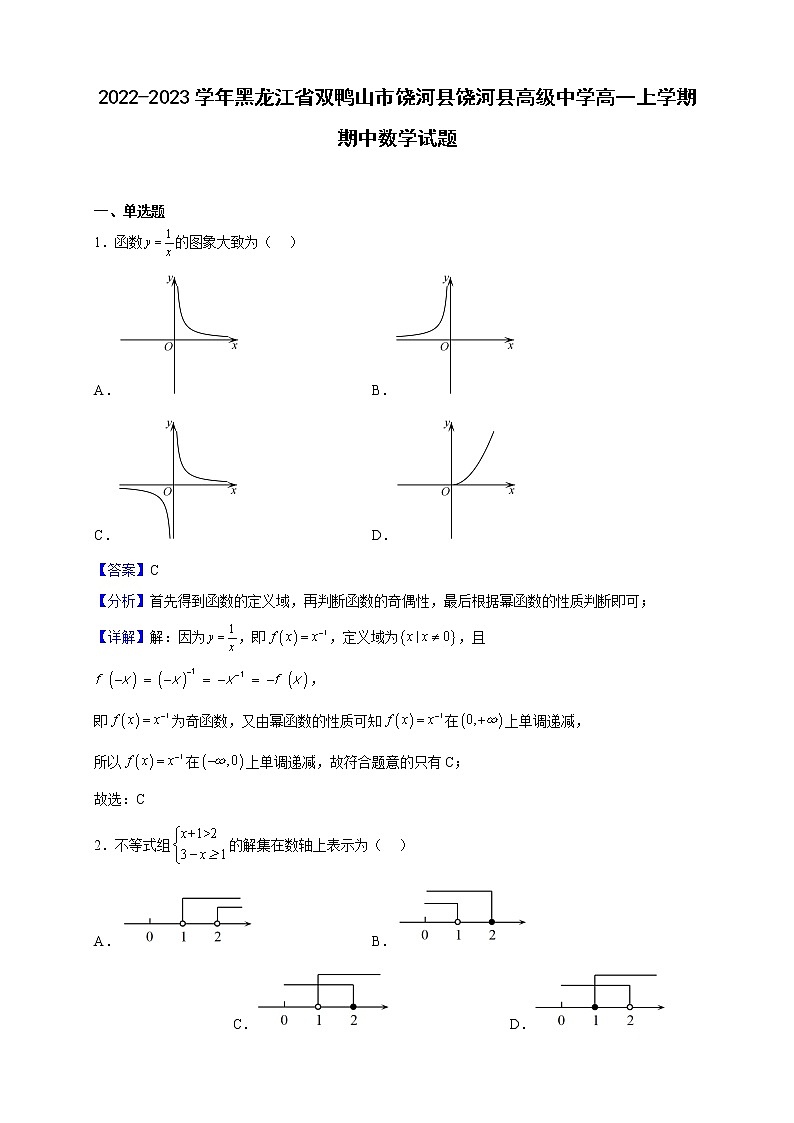
1．函数的图象大致为（    ）

A． B．

C． D．

【答案】C

【分析】首先得到函数的定义域，再判断函数的奇偶性，最后根据幂函数的性质判断即可；

【详解】解：因为，即，定义域为，且，

即为奇函数，又由幂函数的性质可知在上单调递减，

所以在上单调递减，故符合题意的只有C；

故选：C

2．不等式组的解集在数轴上表示为（    ）

A． B． C． D．

【答案】C

【分析】先解不等式组得出解集，再在数轴上表示出来即可.

【详解】由不等式，解得；

由不等式，解得；

故此不等式组的解集为：，

该不等式组的解集在数轴表示如下：

故选：C

3．命题“”的否定是（    ）

A． B．

C． D．

【答案】C

【分析】全称量词命题的否定，是把全称量词改成存在量词，并把后面的结论否定.

【详解】根据全称量词命题的否定是存在量词命题可得，

命题“”的否定是“”.

故选：C.

4．图中，，分别为幂函数，，在第一象限内的图象，则，，依次可以是（    ）

A．，3， B．，3， C．，，3 D．，，3

【答案】D

【分析】根据幂函数的图象，结合幂函数的性质判断参数的大小关系，即可得答案.

【详解】由题图知：，，，

所以，，依次可以是，，3．

故选：D

5．“”是“”的（    ）

A．充要条件 B．充分不必要条件

C．必要不充分条件 D．既不充分也不必要条件

【答案】B

【分析】本题主要是根据条件判断充分必要性，由所给条件很容易得到答案

【详解】当时，，充分条件成立.

解方程，得或，必要条件不成立.

“”是“”成立的充分不必要条件.

故选：B.

6．已知集合，则集合可化简为（　　）

A． B． C． D．

【答案】A

【分析】解方程，可得集合.

【详解】解方程可得或，则.

故选：A.

7．下列关系式中，正确的是（    ）

A． B． C． D．

【答案】D

【分析】根据元素与集合的关系，集合与集合的关系进行判断即可.

【详解】，所以A错误；

集合是点集，集合{2}数集，没有包含关系，故B错误；

是有理数集，，所以C错误；

空集是任何集合的子集，所以D正确.

故选：D.

8．现有下列函数：①；②；③；④；⑤；⑥；⑦，其中幂函数的个数为（    ）

A．1 B．2 C．3 D．4

【答案】B

【分析】根据幂函数的定义逐个辨析即可

【详解】幂函数满足形式，故，满足条件，共2个

故选：B

9．已知函数，则（    ）

A． B．3 C．1 D．19

【答案】C

【分析】根据解析式直接求解即可.

【详解】因为，

所以，

故选：C

10．完成一项装修工程，请木工需付工资每人50元，请瓦工需付工资每人40元，现有工人工资预算2000元，设木工人，瓦工人，则请工人满足的关系式是（    ）

A． B．

C． D．

【答案】D

【分析】根据工资预算以及工人工资列出不等式.

【详解】依题意，请工人满足的关系式是，

即.

故选：D

11．若不等式对一切恒成立，则的取值范围是（  ）

A． B． C． D．

【答案】C

【分析】讨论二次项系数是否为零，结合判别式符号可得答案.

【详解】当时，原式化为，显然恒成立；

当时，不等式对一切恒成立，

则有且，解得.

综上可得，.

故选：C

12．周末，自行车骑行爱好者甲、乙两人相约沿同一路线从地出发前往地进行骑行训练，甲、乙分别以不同的速度匀速骑行，乙比甲早出发分钟.乙骑行分钟后，甲以原速的继续骑行，经过一段时间，甲先到达地，乙一直保持原速前往地.在此过程中，甲、乙两人相距的路程（单位：米）与乙骑行的时间（单位：分钟）之间的关系如图所示，则下列说法错误的是（    ）

A．乙的速度为米/分钟 B．分钟后甲的速度为米/分钟

C．乙比甲晚分钟到达地 D．、两地之间的路程为米

【答案】C

【分析】首先由图象确定甲乙两人的速度，再求出甲到达地时乙距离的的距离，计算甲的总路程即为、两地之间的路程，进而可判断各个选项的正确性，即可得正确答案.

【详解】因为乙比甲早出发分钟，由图知：乙的速度为米/分钟，故选项A正确；

设甲的原速度为，因为，解得：米/分钟，

所以分钟后甲的速度为米/分钟，故选项B正确；

当时，甲到达地，此时乙距离地还有米，所以还需要分钟，所以乙比甲晚分钟到达地，故选项C

不正确；

、两地之间的路程为米，故选项D正确；

所以说法错误的是选项C，

故选：C.

二、填空题

13．已知为奇函数，当时，则______．

【答案】－12

【分析】利用奇函数的性质即可得到答案.

【详解】因为为奇函数，所以，

故．

故答案为：－12.

14．在上的最小值为______．

【答案】0

【分析】先确定函数的单调性，再根据单调性求最小值即可.

【详解】解: 根据题意在上为增函数，

则在上的最小值为．

故答案为：0.

15．已知函数，若在上单调递减，则的取值范围为______．

【答案】

【分析】由题意可得，解不等式组即可得出答案.

【详解】由题意得,即，

解得：．

所以的取值范围为.

故答案为：.

16．已知，，下面四个结论：

①；②若，则的最小值为4；③若，则；④若，则的最小值为；

其中正确结论的序号是______．（把你认为正确的结论的序号都填上）

【答案】①③④

【分析】对于①，由，得，然后变形后判断，对于②，变形后利用基本不等式判断，对于③，由不等式的性质判断，对于④，将展开由基本不等式可推导出结果

【详解】对于①，因为，所以，即，

因为，，所以，所以①正确，

对于②，因为，所以，

所以

，

当且仅当，，即时取等号，所以②错误，

对于③，因为，所以，因为，所以，所以③正确，

对于④，因为，

当且仅当，即时取等号，

因为，所以，所以，当且仅当时取等号，所以④正确，

故答案为：①③④

三、解答题

17．试比较与的值的大小．

【答案】

【分析】利用作差法判断即可.

【详解】因为

，

所以.

18．（1）已知，求函数的最小值．

（2）已知，，且，求的最小值．

【答案】（1）；（2）．

【分析】（1）根据，利用基本不等式可求得最小值；

（2）根据，配凑出符合基本不等式的形式，利用基本不等式可求得最小值.

【详解】（1），，

（当且仅当，即时取等号），

的最小值为；

（2），，

，，，，

（当且仅当，即，时取等号），

的最小值为.

19．（1）解不等式.

（2）若不等式的解集为，求实数，的值；

【答案】（1）不等式的解集为或;（2）,.

【分析】（1）根据一元二次不等式的解法即可求出；

（2）根据函数与方程的思想即可求出.

【详解】（1）即为,而的两根为,所以不等式的解集为或.

（2）由题意可知的两根为,所以,

,解得,.

20．（1）已知函数，求函数的解析式

（2）已知为一次函数，若，求的解析式.

【答案】（1）；（2）或.

【分析】（1）根据给定关系式，利用配凑法求解作答.

（2）设出函数的解析式，再利用待定系数法求解作答.

【详解】（1）函数，则，

所以函数的解析式是.

（2）因为一次函数，设，

则，而，

于是得，解得或，

所以或.

21．已知函数．

(1)画出函数的图象；

(2)当≥2时，求实数x的取值范围．

【答案】(1)作图见解析

(2)

【分析】（1）根据解析式各分段的解析式，在坐标系中描点，进而画出图象.

（2）由题设知：或求解即可.

【详解】（1）由解析式知：

∴的图象如下图示：

（2）由题可得：或，解得或，

∴实数x的取值范围为．

22．已知函数．

(1)当时，求的单调区间不要求证明；

(2)若为偶函数，求a的值；

(3)若的最小值，求实数a的取值范围．

【答案】(1)在上单调递减，在上调递增

(2)

(3)或

【分析】（1）当时，，即可得的单调区间；

（2）由条件可得恒成立，即可求得的值；

（3），分类讨论得的最小值，根据求得实数的取值范围即可．

【详解】（1）当时，，

∴在上单调递减，在上调递增．

（2）因为定义域为，，

所以恒成立，解得．

（3）．

①当时，时，，解得．

②当即时，，解得．

③当，即时，，解得或，

∴．

综上可得，或．