2022-2023学年黑龙江省饶河县高级中学高一上学期12月月考数学试题（解析版）

这是一份2022-2023学年黑龙江省饶河县高级中学高一上学期12月月考数学试题（解析版），共12页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．函数的图象大致为（ ）
A．B．
C．D．
【答案】A
【分析】由单调性和所过定点作出判断.
【详解】因为，所以单调递增，且恒过点，
故A为正确答案.
故选：A
2．下列函数中，增长速度最快的是（ ）
A．B．
C．D．
【答案】A
【解析】直接根据一次函数，幂函数，对数函数和指数函数的增长差异判断.
【详解】是一次函数，是幂函数，是对数函数，是指数函数，
因为当x足够大时，指数函数增长速度最快，
故选：A.
3．下列函数是对数函数的是（ ）
A．B．
C．（，）D．
【答案】B
【分析】根据对数函数的定义，即可判断选项.
【详解】对于A，真数为，而不是，故A不是对数函数；
对于B，底数为常数，且，真数为，且函数系数为1，故B是对数函数；
对于C，真数为常数，而不是，故C不是对数函数；
对于D，真数为，而不是，故D不是对数函数．
故选：B．
4．与角终边相同的角可以表示为（ ）
A． B．
C．D．
【答案】A
【分析】先求出相近的终边相同的角，即可判断.
【详解】与角终边相同的角为，故与角终边相同的角可以表示为.
故选：A
5．已知，则（ ）
A．a【答案】A
【解析】找中间量0或1进行比较大小，可得结果
【详解】，所以，
故选：A.
【点睛】此题考查利用对数函数、指数函数的单调性比较大小，属于基础题
6．当时，，，的大小关系是
A．B．
C．D．
【答案】B
【分析】在平面直角坐标系中作出三个函数在区间内的图象，根据图象得到大小关系.
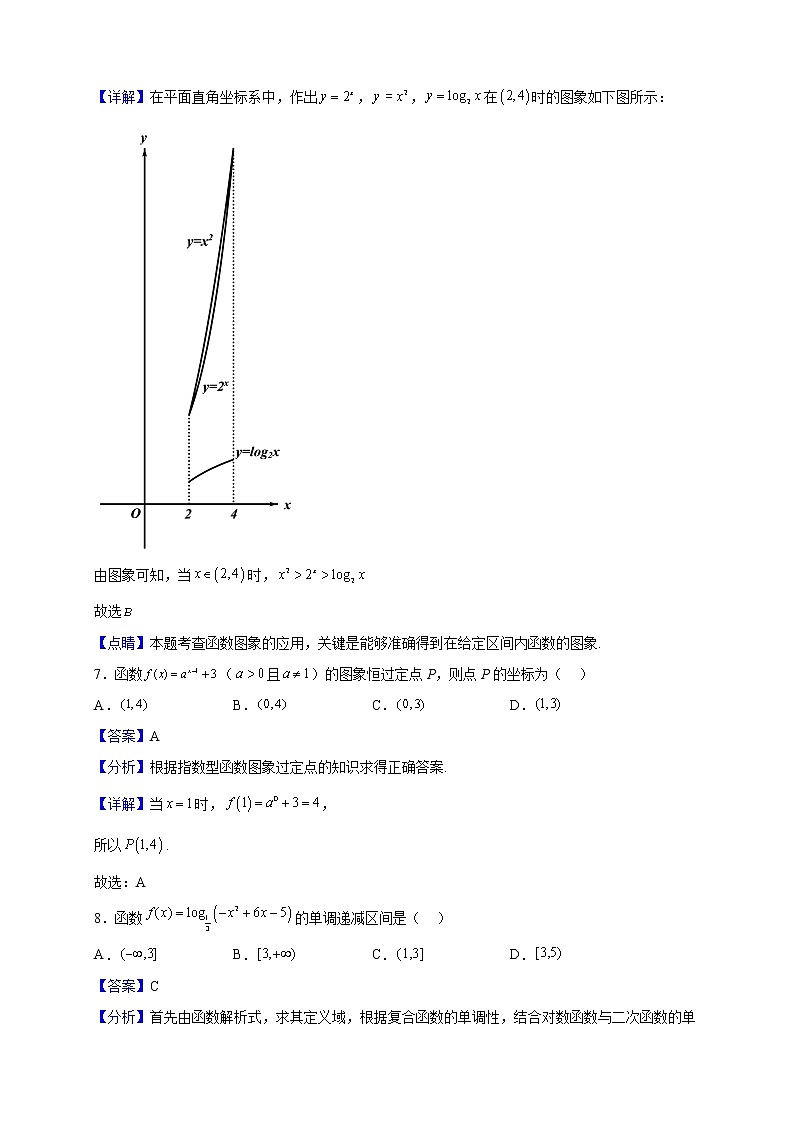
【详解】在平面直角坐标系中，作出，，在时的图象如下图所示：
由图象可知，当时，
故选
【点睛】本题考查函数图象的应用，关键是能够准确得到在给定区间内函数的图象.
7．函数（且）的图象恒过定点P，则点P的坐标为（ ）
A．B．C．D．
【答案】A
【分析】根据指数型函数图象过定点的知识求得正确答案.
【详解】当时，，
所以.
故选：A
8．函数的单调递减区间是（ ）
A．B．C．D．
【答案】C
【分析】首先由函数解析式，求其定义域，根据复合函数的单调性，结合对数函数与二次函数的单调性，可得答案.
【详解】由，则，，解得，即函数的定义域，
由题意，令，，则，
易知在其定义域上单调递减，要求函数的单调递减区间，需求在上二次函数的递增区间，
由，则在上二次函数的递增区间为，
故选：C.
9．若函数的一个零点（正数）附近的函数值用二分法逐次计算，参考数据如下表：那么方程的一个近似解（精确度0.04）为（ ）
A．1.5B．1.25C．1.375D．1.4375
【答案】D
【分析】根据零点存在定理判断求解．
【详解】由表格结合零点存在定理知零点在上，区间长度为0.03125，满足精度要求，观察各选项，只有D中值1.4375是该区间的一个端点，可以作为近似解，
故选：D．
10．已知，则的值为（ ）
A．2B．－2C．D．±2
【答案】D
【分析】利用与的关系求解即可.
【详解】，所以
故选：D
11．冈珀茨模型是由冈珀茨（Gmpertz）提出的，可作为动物种群数量变化的模型，也可用于描述种群的消亡规律.已知某珍稀物种年后的种群数量近似满足冈珀茨模型（，当时表示2022年初的种群数量），经过年后，当该物种的种群数量不足2022年初种群数量的时，即将有濒临灭绝的危险，则的最小值为（参考数据：）（ ）
A．10B．11C．12D．13
【答案】D
【分析】根据题意列出不等式求出的取值范围，即可得到的最小值.
【详解】根据题意得时2022年初种群数量为，
所以，
化简得，则，
又因为，所以的最小值为13.
故选：D.
12．若关于x的方程有解，则实数的取值范围为( )
A．B．C．D．
【答案】C
【分析】将对数方程化为指数方程，用x表示出a，利用基本不等式即可求a的范围．
【详解】，
，
当且仅当时取等号，
故．
故选：C．
二、填空题
13．已知函数恒过定点，则此定点为__________.
【答案】
【分析】根据对数函数的性质，令求解.
【详解】由，
解得，
所以函数过定点，
故答案为：
14．函数f（x）＝lg2（x2＋2x－3）的定义域是______．
【答案】
【分析】由真数大于0，解不等式可得.
【详解】由x2＋2x－3＞0，解得x＞1或x＜－3，
故答案为：．
15．①函数的图象过定点；
②是方程有两个实数根的充分不必要条件；
③的反函数是，则；
④已知在区间上单调递减，则实数a的取值范围是.
以上结论正确的是___________.
【答案】①④
【分析】根据指数型函数过定点、充分不必要条件、反函数、对数型复合函数单调性的知识确定正确答案.
【详解】①，当时，，所以过定点，①正确
②，方程有两个实数根.，与有两个交点，结合图象可知，.
所以是方程有两个实数根的必要不充分条件，②错误.
③，的反函数是，③错误.
④，在区间上单调递减，
则，所以④正确.
故答案为：①④
16．已知，函数，其中是自然对数的底数．若函数有且仅有三个零点，则实数a的取值范围是______．
【答案】
【分析】首先作出的函数图像，令，将零点问题转化为二次函数零点，再一步转化为与的图像交点问题，结合图像分析的范围，即可间接求出参数的范围.
【详解】令,则的有且仅有三个零点，等价于与的图像有且仅有三个交点.
①当只有一解时，此时，即.而时，代入，解得，此时与没有三个交点，舍去；当时，代入解得，由图像可知，此时与图像有有三个交点，符合题意，;
②当有两个解时，即或.设解分别为和，则与以及两条直线有三个交点即可.，当时，由图形可知，不符合题意，故，此时.当，时，此时函数图像共有三个交点，则此时，由韦达定理知，，解得，与矛盾，不符合题意；当，时，由二次函数根分布的条件可知有，解得.
综上所述，有三个零点时，范围为.
故答案为：
三、解答题
17．计算：
(1)．
(2)．
【答案】(1)．
(2)．
【分析】利用指数、对数的运算性质可得解.
【详解】（1）
（2）
.
18．（1）若，求的值；
（2）设，用表示．
【答案】（1）；（2）.
【分析】（1）利用指数幂的运算性质求解；
（2）利用换底公式以及对数的运算性质求解．
【详解】（1）∵，
∴．
（2），根据换底公式，
∴．
19．函数在区间和内各有一个零点，求实数的取值范围.
【答案】
【分析】利用二次函数的零点分布求解.
【详解】因为函数在区间和内各有一个零点，
所以，
解得.
20．已知函数（且）的图象过点．
(1)求a的值；
(2)若，求的定义域并判断其奇偶性和单调递增区间．
【答案】(1)
(2)定义域为，在上单调递增，单调递增区间为
【分析】（1）根据给定条件结合指数式与对数式的互化计算作答.
（2）由（1）求出的解析式，列不等式求定义域，利用奇偶性定义判断作答.
【详解】（1）解：（1）由条件知，即，又且，∴．
（2）（2）．①由，得
，∴的定义域为．∵，
∴是偶函数；②，
∵函数单调递增，函数在上单调递增，故的单调递增区间为．
21．已知函数
(1)求和的值
(2)若函数，试讨论函数的零点个数.
【答案】(1)，
(2)答案见解析.
【分析】（1）根据解析式直接求解即可，
（2）函数的零点个数就是的图象与直线交点的个数，作出函数的图象，结合图象求解即可.
【详解】（1）因为，
所以，，
（2）根据题意零点的个数，即为的图象与直线交点的个数，
函数的图象如图所示，
由图象可知，当或时，的图象与直线有2个交点，即有2个零点，
当时，的图象与直线有3个交点，即有3个零点，
当时，的图象与直线有1个交点，即有1个零点，
综上，当或时，有2个零点；当时，有3个零点；当时，有1个零点.
22．已知是定义在R的偶函数，且，．
(1)求的解析式；
(2)设，若存在，对任意的，都有，求实数t的取值范围．
【答案】(1)
(2)
【分析】（1）由求得，从而求得.
（2）求得在区间上的最小值，对进行分类讨论，求得在区间上的最小值，根据求得的取值范围.
【详解】（1）是定义在R的偶函数，
所以，，
，
此时，满足题意，
所以，
（2）依题意存在，对任意的，都有，
，
在区间上递增，在区间上的最小值为.
，开口向上，对称轴为，
当时，在上递增，最小值为，
依题意可知，则.
当时，的最小值为，
依题意可知，则.
当时，在上递减，最小值为，
依题意可知，不符合.
综上所述，的取值范围是.
【点睛】利用函数的奇偶性求参数，可以利用特殊点代入法进行求解.求解二次函数在闭区间上的最值，当函数含有参数时，要对参数进行分类讨论.