



第02讲 与三角形有关的角(2大考点7种解题方法)2022-2023学年八年级数学考试满分全攻略(人教版)
展开第02讲 与三角形有关的角(2大考点7种解题方法)
一.三角形内角和定理
(1)三角形内角的概念:三角形内角是三角形三边的夹角.每个三角形都有三个内角,且每个内角均大于0°且小于180°.
(2)三角形内角和定理:三角形内角和是180°.
(3)三角形内角和定理的证明
证明方法,不唯一,但其思路都是设法将三角形的三个内角移到一起,组合成一个平角.在转化中借助平行线.
(4)三角形内角和定理的应用
主要用在求三角形中角的度数.①直接根据两已知角求第三个角;②依据三角形中角的关系,用代数方法求三个角;③在直角三角形中,已知一锐角可利用两锐角互余求另一锐角.
(5)直角三角形两个锐角互余.
二.三角形的外角性质
(1)三角形外角的定义:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
三角形共有六个外角,其中有公共顶点的两个相等,因此共有三对.
(2)三角形的外角性质:
①三角形的外角和为360°.
②三角形的一个外角等于和它不相邻的两个内角的和.
③三角形的一个外角大于和它不相邻的任何一个内角.
(3)若研究的角比较多,要设法利用三角形的外角性质②将它们转化到一个三角形中去.
(4)探究角度之间的不等关系,多用外角的性质③,先从最大角开始,观察它是哪个三角形的外角.
考点精讲
考点考向
考点一:三角形内角和定理
题型一:三角形内角和定理证明
一、填空题
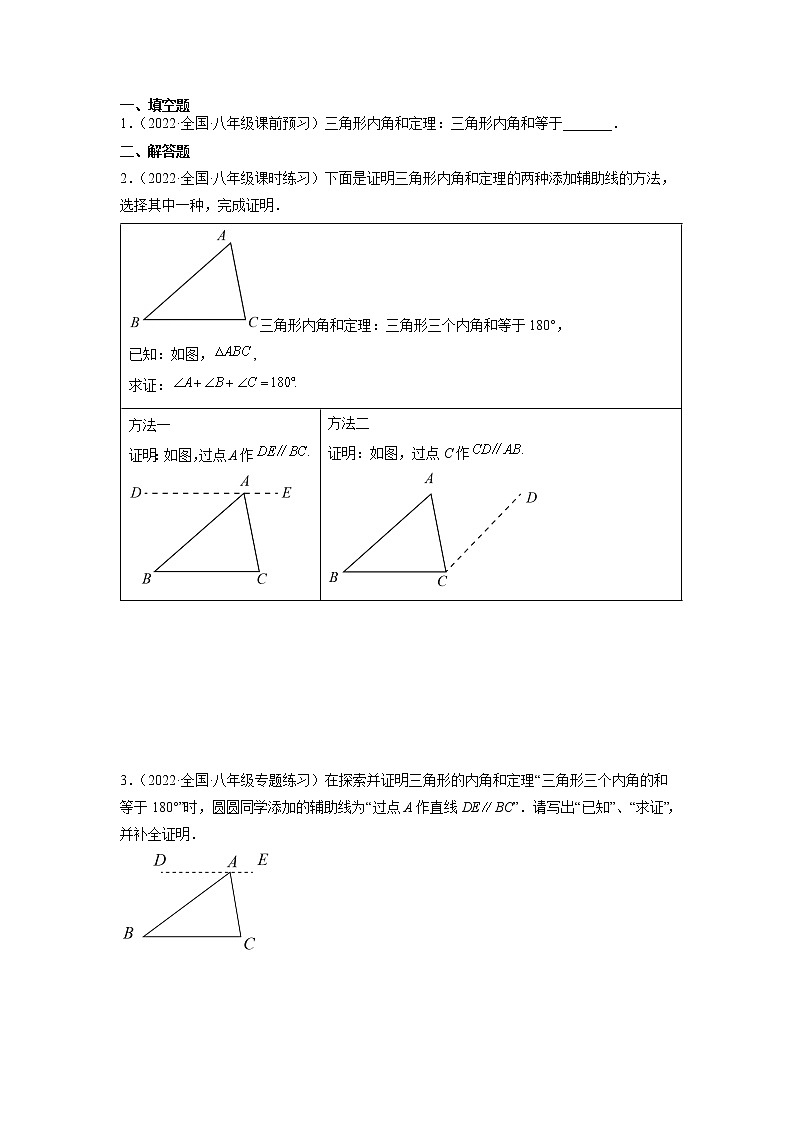
1.(2022·全国·八年级课前预习)三角形内角和定理:三角形内角和等于_______.
二、解答题
2.(2022·全国·八年级课时练习)下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.
三角形内角和定理:三角形三个内角和等于180°,
已知:如图,,
求证:
方法一
证明:如图,过点A作
方法二
证明:如图,过点C作
3.(2022·全国·八年级专题练习)在探索并证明三角形的内角和定理“三角形三个内角的和等于180°”时,圆圆同学添加的辅助线为“过点A作直线DEBC”.请写出“已知”、“求证”,并补全证明.
4.(2021·广西·靖西市教学研究室八年级期末)(1)如图①,直线DE经过点A,DE∥BC.若∠B=45°,∠C=58°,那么∠DAB= ;∠EAC= ;∠BAC= .(在空格上填写度数)
(2)求证:在△ABC中,∠A+∠B+∠C=180°.
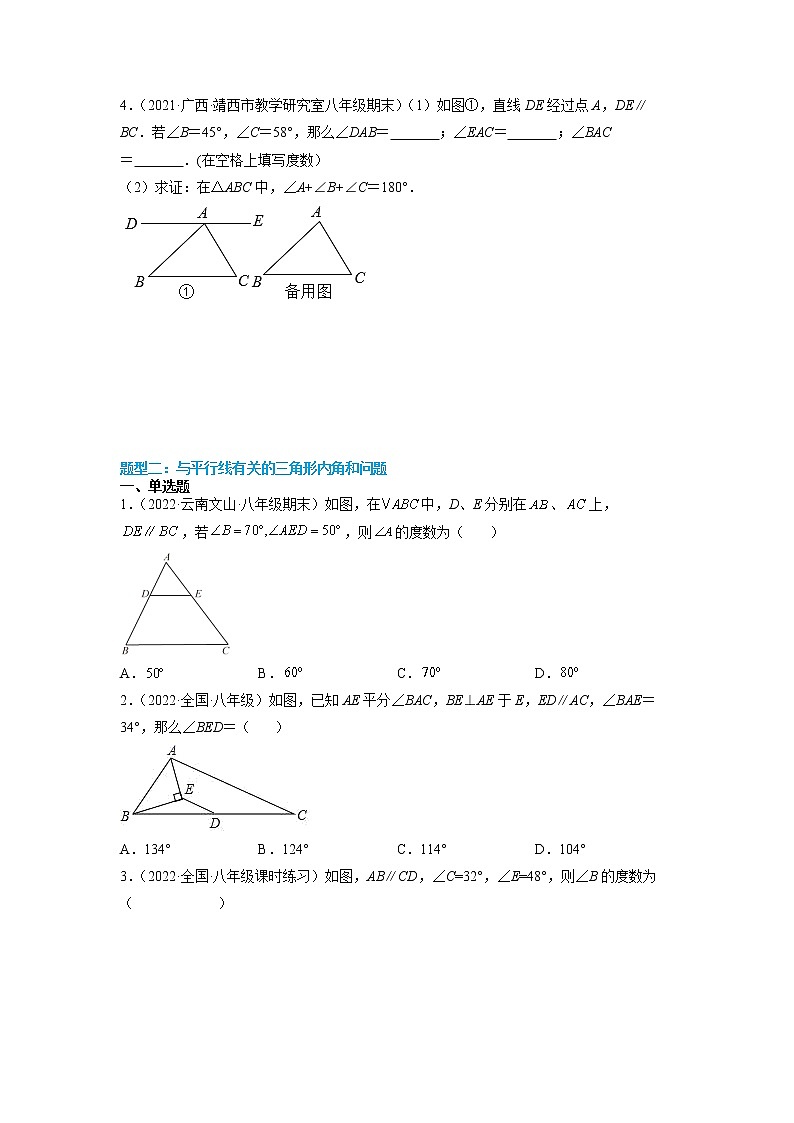
题型二:与平行线有关的三角形内角和问题
一、单选题
1.(2022·云南文山·八年级期末)如图,在中,D、E分别在、上,,若,则的度数为( )
A. B. C. D.
2.(2022·全国·八年级)如图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=34°,那么∠BED=( )
A.134° B.124° C.114° D.104°
3.(2022·全国·八年级课时练习)如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )
A.120° B.128° C.110° D.100°
二、填空题
4.(2022·江西·赣州市赣县区教育教学研究室八年级期末)如图,AB∥CD,,,则_______.
5.(2022·全国·八年级课时练习)如图所示,在中,,点D在边上,.若,则_____度.
三、解答题
6.(2022·全国·八年级专题练习)如图,已知,且.
(1)求证:,请完成下面的证明:
∵,,
∴
∴(___________________),
∴___________________(___________________),
又∵(已知),
∴(___________________),
∴(同位角相等,两直线平行)
∴(___________________);
(2)若平分,且,,求的度数.
题型三:与角平分线有关的三角形内角和问题
一、单选题
1.(2022·浙江·八年级专题练习)如图,已知△ABC中,BD,CE分别是△ABC的角平分线,BD与CE交于点O,如果∠A=54°,那么∠BOC的度数是( )
A.97° B.117° C.63° D.153°
2.(2022·浙江·八年级专题练习)如图,在△ABC中,BD平分∠ABC,DEBC交AB于点E.若∠A=70°,∠BDC=100°,则∠BED的度数为( )
A.120° B.130° C.140° D.150°
二、填空题
3.(2022·河南郑州·八年级期末)如图所示,△中,,BP,CP,BM,CM分别是∠ABC,∠ACD,∠PBC,∠PCB的平分线,则∠M的度数为______.
三、解答题
4.(2022·陕西渭南·八年级期末)如图,在ABC中,AN平分∠BAC交BC于N,∠B=50°,∠ANC=80°,求∠C的度数.
5.(2022·浙江·八年级专题练习)已知:如图,△ABC中,AD⊥BC于点D,BE是∠ABC的平分线,若∠DAC=30°,∠BAC=80°.
(1)求∠EBC的度数;
(2)求∠AOB的度数.
6.(2022·河南郑州·八年级期末)如图,在中,,,AE平分∠BAC.
(1)计算:若,,求∠DAE的度数;
(2)猜想:若,则______;
(3)探究:请直接写出∠DAE,∠C,∠B之间的数量关系.
7.(2022·全国·八年级专题练习)如图,在中,BO,CO是的内角平分线且BO,CO相交于点O.
(1)若,,求∠BOC的度数.
(2)若,求∠BOC的度数.
(3)请你直接写出∠A与∠BOC满足的数量关系式,不需要说明理由.
题型四:三角形折叠中角度问题
一、单选题
1.(2022·全国·八年级课时练习)如图,在△ABC中,∠A=30°,∠B=50°,将点A与点B分别沿MN和EF折叠,使点A、B与点C重合,则∠NCF的度数为( ).
A.22° B.21° C.20° D.19°
二、填空题
2.(2022·全国·八年级课时练习)如图,将直角三角形纸片ABC进行折叠,使直角顶点A落在斜边BC上的点E处,并使折痕经过点C,得到折痕CD.若∠CDE=70°,则∠B=______°.
3.(2022·全国·八年级课时练习)如图,把三角形纸片沿折叠,使点落在四边形外部,那么,,之间的数量关系是________.
4.(2022·全国·八年级课时练习)一个四边形纸片ABCD,∠B=∠D,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,若∠C=86°,那么∠AEB=__°.
5.(2022·全国·八年级课时练习)如图,在中,点是边上的一点,,,将沿折叠得到,与交于点,则 ______度.
6.(2022·全国·八年级课时练习)如图,射线AB与射线CD平行,点F为射线AB上的一定点,连接CF,点P是射线CD上的一个动点(不包括端点C),将沿PF折叠,使点C落在点E处.若,当点E到点A的距离最大时,_____.
题型五:三角形内角和定理的应用
一、单选题
1.(2022·浙江·八年级专题练习)如图,已知,若∠B=120°,∠D=20°,那么∠DCE的度数为( )
A.80° B.90° C.100° D.110°
2.(2021·海南省直辖县级单位·八年级期中)在中,,则的度数为( )
A. B. C. D.
3.(2022·浙江·八年级专题练习)若三角形三个内角度数之比为2:3:5,则这个三角形一定是( )
A.等腰直角三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
4.(2022·河南信阳·八年级期末)如图,,一块含角的直角三角板的一个顶点落在其中一条直线上,若,则的度数为( )
A. B. C. D.
二、填空题
5.(2022·陕西西安·八年级期末)已知中,,,则的度数为______.
三、解答题
6.(2022·河北张家口·八年级期末)如图所示,有一块直角三角板DEF(足够大),其中∠EDF=90°,把直角三角板DEF放置在锐角△ABC上,三角板DEF的两边DE、DF恰好分别经过B、C.
(1)若∠A=40°,则∠ABC+∠ACB= °,∠DBC+∠DCB= °,∠ABD+∠ACD= °.
(2)若∠A=55°,则∠ABD+∠ACD= °.
(3)请你猜想一下∠ABD+∠ACD与∠A所满足的数量关系.
7.(2022·河南三门峡·八年级期末)如图,在△ABC中,BD平分∠ABC,CE平分∠ACB,BD与CE相交于点O,∠BOC=119°.
(1)求∠OBC+∠OCB的度数;
(2)求∠A的度数.
8.(2022·贵州铜仁·八年级期末)如图,在中,.
(1)求的取值范围;
(2)若,,,求的度数.
题型六:直角三角形两个锐角互余
一、填空题
1.(2022·河南安阳·八年级期末)若直角三角形的两锐角之差为,则较大一个锐角的度数是___________度.
2.(2022·广西崇左·八年级期末)如图,,于点,于点,若,则__________.
二、解答题
3.(2021·海南省直辖县级单位·八年级期中)如图,在中,于D,平分,求的度数.
4.(2021·广西贺州·八年级期中)如图,AD是△ABC的BC边上的高,AE平分∠BAC,BF平分∠ABC,BF与AE相交于点O若∠ABC=42°,∠C=72°,求∠AEC和∠DAE的度数.
5.(2022·河南驻马店·八年级期末)如图,AD∥BE,,.求证:.
6.(2022·湖北荆州·八年级期末)如图,在△ABC中,CD是AB边上高,BE为角平分线,若∠BFC=112°,求∠BCF的度数.
7.(2022·安徽淮北·八年级期末)如图,AD是的角平分线,AE是的高,已知,,求的度数.
考点二:三角形外角和
题型七:三角形外角的定义及性质
一、单选题
1.(2021·四川·树德中学八年级开学考试)如图,直线CE∥DF,∠CAB=125°,∠ABD=85°,则∠1+∠2=( )
A.30° B.35° C.36° D.40°
2.(2022·河北张家口·八年级期末)如果将一副三角板按如图的方式叠放,则∠1的度数为( )
A.105° B.120° C.75° D.45°
3.(2022·浙江·八年级专题练习)如图,直线,点A在直线a上,点C、D在直线b上,且AB⊥BC,BD平分∠ABC,若∠1=32°,则∠2的度数是( )
A.13° B.15° C.14° D.16°
4.(2022·浙江·八年级专题练习)如图,在Rt△ABC中,∠BAC=90°,AD平分∠BAC交BC边于点D,若∠C=26°,则∠ADB的度数是( )
A.61° B.64° C.71° D.109°
5.(2022·广东广州·八年级期末)如图,,∠A=45°,∠C=∠E,则∠C的度数为( )
A.45° B.22.5° C.67.5° D.30°
二、填空题
6.(2022·四川凉山·八年级期末)如图,在△ABC中,∠C=47°,将△ABC沿着直线折叠,点C落在点D的位置,则∠1-∠2的度数是________.
三、解答题
7.(2022·河南郑州·八年级期末)在学习完《7.5三角形内角和定理》,小芳和同学们作如下探究:
已知:在中,,分别是的边,上的点,点是边上的一个动点,令,.
(1)他们探究得到:四边形的内角和是.
理由如下:如图①,连接,
在和中,
,
( ).
( ).
.
即四边形的内角和是.
(2)如图①,点在线段上,且,求的度数.
(3)如果点运动到的延长线上,请在图②中补全图形,并直接写出,,之间的等量关系.
8.(2022·浙江·八年级专题练习)【概念认识】
如图①,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD,BE叫做∠ABC的“三分线”.其中,BD是“邻BA三分线”,BE是“邻BC三分线”.
【问题解决】
(1)如图②,在△ABC中,∠A=70°,∠ABC=45°,若∠ABC的邻BA三分线BD交AC于点D,则∠BDC的度数为________;
(2)如图③,在△ABC中,BP,CP分别是∠ABC邻BC三分线和∠ACB邻CB三分线,且∠BPC=135°,求∠A的度数;
【延伸推广】
(3)在△ABC中,∠ACD是△ABC的外角,∠B的邻BC三分线所在的直线与∠ACD的三分线所在的直线交于点P.若∠A=m°,∠B=60°,直接写出∠BPC的度数.(用含m的代数式表示)
巩固提升
一.选择题(共8小题)
1.(2022•珙县校级模拟)已知,在△ABC中,∠C=56°,点D在线段BA的延长线上,过点D作DF⊥BC,垂足为F,若∠FDB=20°,则∠CAB的度数为( )
A.76° B.65° C.56° D.54°
2.(2022•百色一模)任意三角形的外角和是( )
A.180° B.270° C.360° D.540°
3.(2022春•泗水县期末)如图,CE是△ABC的外角∠ACD的平分线,若∠B=30°,∠ACE=60°,则∠A=( )
A.60° B.100° C.90° D.80°
4.(2021秋•城固县期末)如图,图中x的值为( )
A.40 B.50 C.60 D.70
5.(2022春•澄海区期末)如图,线段AB、CD相交于点O,连接AD、CB,∠DAB和∠BCD的平分线AP和CP相交于点P,则∠P与∠D、∠B之间存在的数量关系为( )
A.∠P=2(∠B﹣∠D) B.
C. D.
6.(2022春•新泰市期末)如图,在△ABC中,∠B=50°,AE是∠BAC的平分线,外角∠ACD=100°,则∠AEC的度数为( )
A.65° B.70° C.75° D.50°
7.(2021秋•宜城市期末)在△ABC中,∠B=45°,∠C的外角等于100°,则∠A的度数是( )
A.65° B.55° C.54° D.35°
8.(2021秋•滑县期末)将一副三角板按如图所示放置,则∠BFD的度数为( )
A.105° B.95° C.85° D.75°
二.填空题(共6小题)
9.(2022春•曲阳县期末)如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,∠AOB=125°,则∠CAD的度数为 .
10.(2022春•阜新县期末)Rt△ABC的一个锐角是65°,则另一个锐角是 .
11.(2022春•江源区期末)在△ABC中,∠A=90°,∠B﹣∠C=14°,则∠B= °,∠C= °.
12.(2021秋•威县期末)如图,AD是△ABC的BC边上的高,AE是∠BAC的角平分线.
(1)若∠B=47°,∠C=73°,则∠DAE的度数为 .
(2)若∠B=α°,∠C=β°(α<β),用含α、β的代数式表示∠DAE的度数= .
13.(2022春•招远市期末)如图,在△ABC中,AD是BAC的平分线,EF∥AD,交BC于E、AB于F、CA的延长线于G,∠B=30°,∠C=70°,则∠G的度数 .
14.(2022春•桂林期末)在△ABC中,若∠C=90°,∠B=54°,则∠A的度数为 .
三.解答题(共10小题)
15.(2022春•鼓楼区校级期末)如图,在△ABC中,∠1=∠2=36°,∠3=∠4,求∠DAC的度数.
16.(2022春•交城县期末)如图,直线AB⊥CD于点G,交EF于点H,射线GM交EF于点M,已知∠AGM:∠DGM=2:7,∠AHF比∠DGM大10°,求∠GHM的度数.
17.(2022春•卧龙区期末)如图,在△ABC中,∠B=25°,∠BAC=31°,过点A作BC边上的高,交BC的延长线于点D,CE平分∠ACD,交AD于点E.求∠AEC的度数.
18.(2022春•耒阳市期末)如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=70°,∠BAC=80°.
求:(1)∠B的度数;
(2)∠C的度数.
19.(2022春•冠县期末)如图,在△ABC中,AN平分∠BAC交BC于N,∠B=50°,∠ANC=80°.求∠C的度数.
20.(2022春•阳谷县期末)(1)探究一:如图(a),BD平分∠ABC,CD平分∠ACB,请确定∠A与∠D的数量关系,并说明理由;
(2)探究二:如图(b),BE平分∠ABC,CE平分∠ACM,请确定∠A与∠E的数量关系 ;
(3)探究三:如图(c),BF平分∠CBP,CF平分∠BCQ,请确定∠A与∠F的数量关系 ;
解决问题:如图,在△ABC中,∠A=56°,BD,CD分别平分∠ABC,∠ACB,M,N,Q分别在DB,DC,BC的延长线上,BE,CE分别平分∠MBC,∠BCN,BF,CF分别平分∠EBC,∠ECQ,则∠F= .
21.(2022春•鼓楼区校级期末)如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)若∠B=35°,∠E=25°,求∠CAE的度数;
(2)证明:∠BAC=∠B+2∠E.
22.(2021秋•礼泉县期末)我们将内角互为对顶角的两个三角形称为“对顶三角形”.例如,在图1中,△AOB的内角∠AOB与△COD的内角∠COD互为对顶角,则△AOB与△COD为“对顶三角形”,根据三角形内角和定理知“对顶三角形”有如下性质:∠A+∠B=∠C+∠D.
(1)如图1,在“对顶三角形”△AOB与△COD中,∠AOB=70°,则∠C+∠D= °.
(2)如图2,在△ABC中,AD、BE分别平分∠BAC和∠ABC,若∠C=60°,∠ADE比∠BED大6°,求∠BED的度数.
23.(2021秋•峡江县期末)材料阅读:如图(1)所示的图形,像我们常见的学习用品—圆规,我们常把这样的图形叫做“规形图”.
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;
(2)请你利用此结论,解决以下两个问题:
Ⅰ.如图(2),把一个三角尺DEF放置在△ABC上,使三角尺的两条直角边DE,DF恰好经过点B,C,若∠A=30°,则∠ABD+∠ACD= .
Ⅱ.如图(3),BD平分∠ABP,CD平分∠ACP,若∠A=50°,∠BPC=130°,求∠BDC的度数.
24.(2022春•冠县期末)某同学在学习过程中,对教材的一个有趣的问题做如下探究:
【习题回顾】
已知:如图1,在△ABC中,角平分线BO、CO交于点O.求∠BOC的度数.
(1)若∠A=40°,请直接写出∠BOC= ;
【变式思考】
(2)若∠A=α,请猜想∠BOC与α的关系,并说明理由;
【拓展延伸】
(3)已知:如图2,在△ABC中,角平分线BO、CO交于点O,OD⊥OB,交边BC于点D,点E在CB的延长线上,作∠ABE的平分线交CO的延长线于点F.若∠F=β,猜想∠BAC与β的关系,并说明理由.
第11讲 乘法公式(4大考点)2022-2023学年八年级数学考试满分全攻略(人教版): 这是一份第11讲 乘法公式(4大考点)2022-2023学年八年级数学考试满分全攻略(人教版),文件包含第11讲乘法公式4大考点解析版docx、第11讲乘法公式4大考点原卷版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
第10讲 整式的乘法(7大考点)2022-2023学年八年级数学考试满分全攻略(人教版): 这是一份第10讲 整式的乘法(7大考点)2022-2023学年八年级数学考试满分全攻略(人教版),文件包含第10讲整式的乘法7大考点解析版docx、第10讲整式的乘法7大考点原卷版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
第07讲 轴对称、画轴对称图形(3大考点15种解题方法)2022-2023学年八年级数学考试满分全攻略(人教版): 这是一份第07讲 轴对称、画轴对称图形(3大考点15种解题方法)2022-2023学年八年级数学考试满分全攻略(人教版),文件包含第07讲轴对称画轴对称图形3大考点15种解题方法解析版docx、第07讲轴对称画轴对称图形3大考点15种解题方法原卷版docx等2份试卷配套教学资源,其中试卷共82页, 欢迎下载使用。












