




第01讲 与三角形有关的线段(8大考点13种解题方法)2022-2023学年八年级数学考试满分全攻略(人教版)
展开第01讲 与三角形有关的线段(8大考点13种解题方法)
考点考向
一.三角形
(1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
组成三角形的线段叫做三角形的边.
相邻两边的公共端点叫做三角形的顶点.
相邻两边组成的角叫做三角形的内角,简称三角形的角.
(2)按边的相等关系分类:不等边三角形和等腰三角形(底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形).
(3)三角形的主要线段:角平分线、中线、高.
(4)三角形具有稳定性.
二.三角形的角平分线、中线和高
(1)从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高.
(2)三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.
(3)三角形一边的中点与此边所对顶点的连线叫做三角形的中线.
(4)三角形有三条中线,有三条高线,有三条角平分线,它们都是线段.
(5)锐角三角形的三条高在三角形内部,相交于三角形内一点,直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.
三.三角形的稳定性
当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.这一特性主要应用在实际生活中.
四.三角形三边关系
(1)三角形三边关系定理:三角形两边之和大于第三边.
(2)在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.
(3)三角形的两边差小于第三边.
(4)在涉及三角形的边长或周长的计算时,注意最后要用三边关系去检验,这是一个隐藏的定时炸弹,容易忽略.
考点精讲
考点一:三角形的认识
题型一:三角形的识别与有关概念
一、单选题
1.(2022·全国·八年级)学习完三角形的概念后,小强同学用火柴拼成的图形如下,其中符合三角形概念的是( )
A. B. C. D.
【答案】C
【分析】根据三角形的概念一一辨析可得正确解答.
【详解】解:三角形指的是不在同一直线上的三条线段首尾顺次相接所组成的图形,而A、B、D图形的三根火柴都全部没有或者部分没有首尾相接,所以A、B、D都不符合题意,只有C图形是由三根火柴首尾顺次相接而成的,所以C符合三角形概念.
故选C.
【点睛】本题考查三角形的定义,正确理解三角形是不在同一直线上的三条线段首尾顺次相接所组成的图形是解题关键.
二、填空题
2.(2022·全国·八年级专题练习)如图,在△BCE中,边BE所对的角是________,∠CBE所对的边是________;在△AEC中,边AE所对的角是________,∠A为内角的三角形是________.
【答案】 ∠BCE CE ∠ACE △ABD,△ABC,△ACE
【分析】根据的边、角的定义,即可求解.
【详解】解:在△BCE中,边BE所对的角是∠BCE,∠CBE所对的边是CE;
在△AEC中,边AE所对的角是∠ACE,∠AEC所对的边是AC;
∠A为内角的三角形是△ABD,△ABC,△ACE.
故答案为:∠BCE;CE;∠ACE;△ABD,△ABC,△ACE
【点睛】本题考查了三角形的知识,掌握由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形;组成三角形的线段叫做三角形的边;相邻两边的公共端点叫做三角形的顶点;相邻两边组成的角叫做三角形的内角,简称三角形的角是解题的关键.
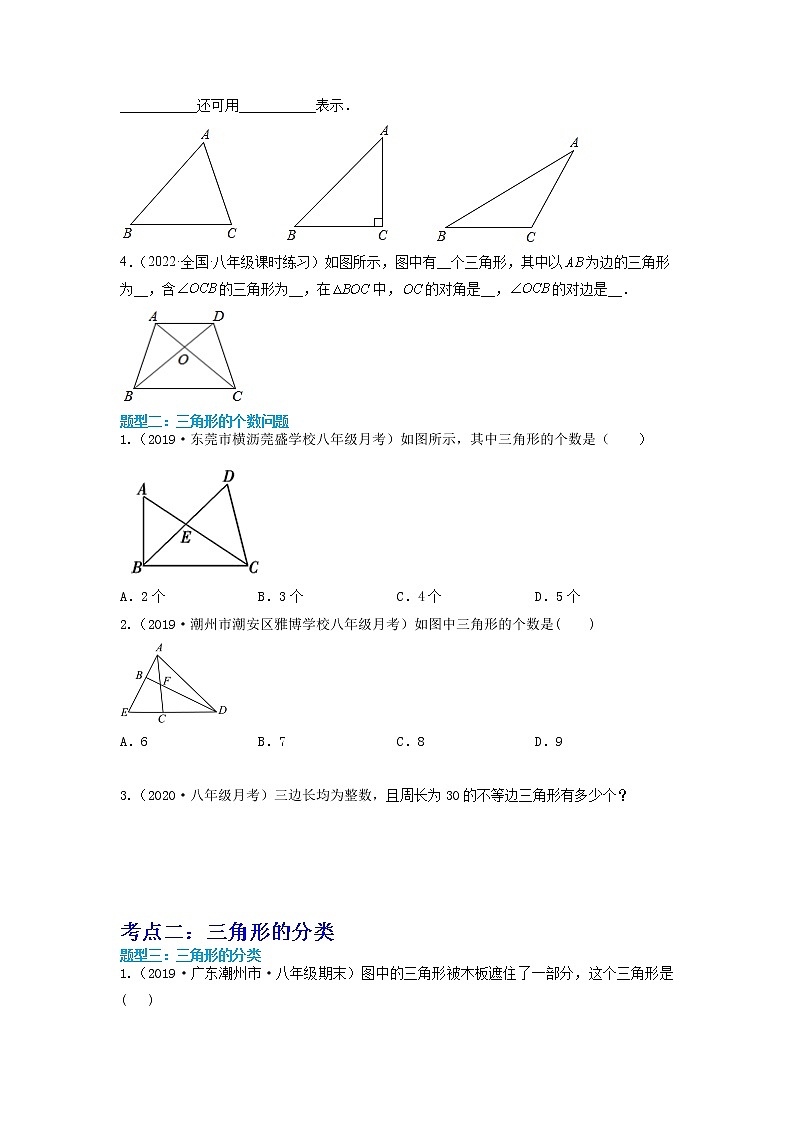
3.(2022·全国·八年级专题练习)如图所示,顶点是A、B、C的三角形,记作___________,读作___________.其中,顶点A所对的边为___________还可用___________表示;顶点B所对的边为___________还可用___________表示;顶点C所对的边为___________还可用___________表示.
【答案】 三角形ABC BC a AC b AB c
【分析】根据三角形的概念进行求解即可.
【详解】解:如图所示,顶点是A、B、C的三角形,记作△ABC,读作三角形ABC.其中,顶点A所对的边为BC还可用a表示;顶点B所对的边为AC还可用b表示;顶点C所对的边为AB还可用c表示.
故答案为:△ABC;三角形ABC;BC;a;AC;b;AB;c.
【点睛】本题主要考查了三角形的概念,解题的关键在于能够熟记概念.
4.(2022·全国·八年级课时练习)如图所示,图中有__个三角形,其中以为边的三角形为__,含的三角形为__,在中,的对角是__,的对边是__.
【答案】 8 ,, ,
【分析】根据三角形的边和角有关概念解答.
【详解】图中有8个三角形,其中以为边的三角形为,,,含的三角形为,,在中,的对角是,的对边是,
故答案为:8;,,;,;;.
【点睛】此题考查三角形,关键是根据三角形的边和角有关概念解答.
题型二:三角形的个数问题
1.(2019·东莞市横沥莞盛学校八年级月考)如图所示,其中三角形的个数是( )
A.2个 B.3个 C.4个 D.5个
【答案】D
【分析】根据三角形的定义解答即可,由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
【详解】图中的三角形有:△ABC,△BCD,△BCE,△ABE,△CDE共5个.
故选D.
【点睛】本题考查了三角形的概念,由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边,相邻边的公共端点叫做三角形的顶点.相邻两条边组成的角,叫做三角形的内角,简称为三角形的角.
2.(2019·潮州市潮安区雅博学校八年级月考)如图中三角形的个数是( )
A.6 B.7 C.8 D.9
【答案】C
【分析】根据三角形的定义得:图中三角形有:△ECA,△EBD,△FBA,△FCD,△AFD,△ABD,△ACD,△AED共8个.
【详解】∵图中三角形有:△ECA,△EBD,△FBA,△FCD,△AFD,△ABD,△ACD,△AED,
∴共8个.
故选C.
【点睛】此题考查了学生对三角形的认识.注意要不重不漏地找到所有三角形,一般从一边开始,依次进行.
3.(2020·八年级月考)三边长均为整数,且周长为30的不等边三角形有多少个?
【答案】18
【分析】不妨设三角形三边为、、,且,由三角形三边关系定理及题设条件可确定的取值范围,以此确定的值,再确定、的值.
【详解】解:设三角形三边为、、,且,
∵,,
∴,即,
∴,
,
∴,
∴,
又∵为整数,
∴为、、、、,
∵①当为时,有1个三角形,,,;
②当为时,有2个三角形,,,;,,;
③当为时,有4个三角形,,,;,,;,,;,,;
④当为时,有5个三角形,,,;,,;,,;,,;,,;
⑤当为时,有7个三角形,,,;,,;,,;,,;
,,;,,;,,;
都是整数的三角形共有19个,其中不等边三角形共有18个.
【点睛】本题主要考查了三角形的三边关系,根据三边关系以及周长正确确定边的范围是解题关键.
考点二:三角形的分类
题型三:三角形的分类
1.(2019·广东潮州市·八年级期末)图中的三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都有可能
【答案】D
【解析】从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角,
故选D.
2.(2020·广东惠州市·)一个等腰三角形的两边长分别为5或6,则这个等腰三角形的周长是_____.
【答案】16或17.
【解析】由于未说明两边哪个是腰哪个是底,故需分两种情况讨论:
(1)当等腰三角形的腰为5,底为6时,周长为5+5+6=16;
(2)当等腰三角形的腰为6,底为5时,周长为5+6+6=17.
∴这个等腰三角形的周长是16或17.
考点三:三角形三边关系
题型四:构成三角形的条件
1.(2021·广东广州市·八年级期末)在下列长度的三条线段中,能围成三角形的是( )
A.2,3,4 B.2,3,5 C.3,5,9 D.8,4,4
【答案】A
【分析】根据三角形的三边关系对各选项中的线段分别进行计算,并作出判断,即可得出结论.
【详解】解:A、2+3>4,能组成三角形,故此选项符合题意;
B、2+3=5,不能够组成三角形,故此选项不符合题意;
C、3+5=8<9,不能组成三角形,故此选项不符合题意;
D、4+4=8,不能组成三角形,故此选项不符合题意.
故选:A.
【点睛】本题考查了三角形的三边关系,掌握三角形三边关系并能准确应用其进行判断是解答此题的关键.
2.(2020·广东)下列长度的三条线段能组成三角形的是( )
A.3,3,4 B.7,4,2 C.3,4,8 D.2,3,5
【答案】A
【分析】看哪个选项中两条较小的边的和大于最大的边即可.
【详解】解:A、3+3>4,能构成三角形,故此选项正确;
B、4+2<7,不能构成三角形,故此选项错误;
C、3+4<8,不能构成三角形,故此选项错误;
D、2+3=5,不能构成三角形,故此选项错误.
故选:A.
【点睛】此题主要考查了三角形的三边关系,在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.
3.(2020·东莞市翰林实验学校八年级期中)下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.,, B.,,
C.,, D.,,
【答案】C
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【详解】解:A、3+4<8,不能组成三角形,不符合题意;
B、8+7=15,不能组成三角形,不符合题意;
C、13+12>20,能够组成三角形,符合题意;
D、5+5<11,不能组成三角形,不符合题意.
故选:C.
【点睛】此题考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.
题型五:确定第三边的取值范围
1.(2021·广东广州市·绿翠现代实验学校八年级期末)如果三角形的两边长分别为2和6,第三边长为偶数,那么这个三角形的周长可以是( )
A.6 B.13 C.14 D.15
【答案】C
【分析】先根据三角形的三边的关系求解第三边的范围,由第三边长为偶数,可得第三边的值,从而可得答案.
【详解】解: 三角形的两边长分别为2和6,设第三边长为,则
<<,
<<,
第三边长为偶数,
,
三角形的周长为:
故选:
【点睛】本题考查的是三角形三边的
2.(2020·深圳市龙岗区百合外国语学校)两根木棒分别为5cm和6cm,要选择第三根,将它们钉成一个三角形,如果第三根木棒长为偶数,则方法有( )
A.3种 B.4种 C.5种 D.6种
【答案】C
【分析】根据三角形的三边关系可求得第三边的取值范围,再求得其中的偶数的个数即可求得答案.
【详解】解:设第三根木棒的长度为xcm,
由三角形三边关系可得6-5<x<6+5,
即1<x<11,
又x为偶数,
∴x的值为2,4,6,8,10,共5种,
故选:C.
【点睛】本题主要考查三角形的三边关系,根据三角形的三边关系求得第三边的取值范围是解题的关键.
关系,三角形周长的计算,掌握三角形三边的关系是解题的关键.
3.(2020·中山市石岐中学八年级期中)已知的两条边长分别为3和5,则第三边c的取值范是________
【答案】2<c<8.
【分析】根据三角形三边关系,可得5-3<c<5+3,即2<c<8,问题可求.
【详解】解:由题意,可得5-3<c<5+3,
即2<c<8,
故答案为:2<c<8
【点睛】此题主要考查了三角形三边关系,熟练掌握三角形的三边关系是解决此类问题的关键.
4.(2020·东莞市厚街海月学校八年级月考)若三角形的三边长分别为3,x-1,7,则x的取值范围为_______________.
【答案】
【分析】根据三角形三边关系:“任意两边之和大于第三边,任意两边之差小于第三边”即可求的取值范围.
【详解】解:由三角形三边关系定理得:,
解得:,
即的取值范围是.
故答案为:.
【点睛】此类求范围的问题,实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.
题型六:三角形三边关系的应用
1.(2021·江苏扬州市·七年级期末)如图,为了估计池塘两岸A、B间的距离,小明在池塘的一侧选一个点P,测得PA=14m,PB=10m,则AB间的距离不可能是( )
A.5m B.15m C.20m D.24m
【答案】D
【分析】根据三角形的三边关系解答.
【详解】解:由题意得,
∴,
故选:D.
【点睛】此题考查三角形三边关系的实际应用,正确理解题意得到三角形三边关系式是解题的关键.
2.(2020·湛江市第二十二中学八年级月考)图①、图②、图③均是的正方形网格,每个小正方形的边长为1,每个小正方形的顶点称为格点,线段的端点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求以为边画.
要求:
(1)在图①中画一个钝角三角形,在图②中画一个直角三角形,在图③中画一个锐角三角形;
(2)三个图中所画的三角形的面积均不相等;
(3)点在格点上.
【答案】见详解(答案不唯一)
【分析】因为点C在格点上,故可将直尺的一角与线段AB点A重合,直尺边长所在直线经过正方形网格左上角第一个格点,继而以点A为旋转中心,逆时针旋转直尺,当直尺边长所在直线与正方形格点相交时,确定点C的可能位置,顺次连接A、B、C三点,按照题目要求排除不符合条件的C点,作图完毕后可根据三角形面积公式判断其面积是否相等.
【详解】经计算可得下图中:图①面积为;图②面积为1;图③面积为,面积不等符合题目要求(2),且符合题目要求(1)以及要求(3).
故本题答案如下:
【点睛】本题考查三角形的分类及其作图,难度较低,按照题目要求作图即可.
考点四:三角形的高
题型七:画三角形的高
1.(2020·东莞市厚街海月学校八年级期中)下列四个图形中,线段BE表示△ABC的高的是( )
A. B.
C. D.
【答案】C
【分析】根据三角形高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高,再结合图形进行判断.
【详解】解:线段BE是△ABC的高的图是选项C.
故选:C.
【点睛】本题考查了三角形的高,三角形的高是指从三角形的一个顶点向对边作垂线,连接顶点与垂足之间的线段.熟记定义是解题的关键.
2.(2019·广州市育才中学八年级期中)△ABC中BC边上的高作法正确的是( )
A. B.
C. D.
【答案】D
【分析】根据三角形高的作法判断即可.
【详解】△ABC中BC边上的高,则从A点向BC边所在直线作垂线,
则D选项符合题意,
故选:D.
【点睛】本题是对三角形高的作法考查,熟练掌握三角形高的作法是解决本题的关键.
题型八:与三角形高有关的计算问题
1.(2021·广东七年级期末)如图,,其中,,,,,则到距离为( )
A.3 B.5 C. D.
【答案】D
【分析】根据三角形高的定义可知,AD长度就是点A到线段BC的距离,根据此解答即可.
【详解】解:∵AB⊥AC,AD⊥BC,
∴BD垂直于AD,
∴B到AD的距离等于BD的长度=BC-CD=,
∴点B到线段AD的距离是,
故选:D.
【点睛】本题主要考查了三角形的高的概念,结合图形找出△ABC边BC上的高是解题的关键.
2.(2020·惠州市第七中学八年级月考)方格纸中每个小正方形的边长均为,点在小正方形的顶点上.
(1)在图中作出边上的高;
(2)求出的面积.
【答案】(1)见解析;(2)6.
【分析】(1)结合格点图,直接利用三角形高线作法得出答案;
(2)结合格点图,直接利用三角形的面积求法得出答案.
【详解】解:(1)如图1所示:DC即为所求;
(2)如图1,.
【点睛】此题主要考查了应用设计与作图以及三角形面积求法,正确得出三角形高线的位置是解题关键.
考点五:三角形的中线
题型九:三角形中线有关求长度问题
1.(2020·永泰县新高博培训学校有限公司九年级月考)如图,AE是△ABC的中线,D是BE上一点,若EC=6,DE=2,则BD的长为( )
A.4 B.3 C.2 D.1
【答案】A
【分析】根据三角形中线定义得BE=EC=6,再由BD=BE-DE求解即可.
【详解】解:∵AE是△ABC的中线,EC=6,
∴BE=EC=6,
∵ DE=2,
∴BD=BE﹣DE=6﹣2=4,
故选:A.
【点睛】本题考查了三角形的中线,熟知三角形的中线定义是解答的关键.
2.如图,△ABC的周长是21cm,AB=AC,中线BD分△ABC为两个三角形,且△ABD的周长比△BCD的周长大6cm,求AB,BC.
【答案】AB=9cm,BC=3cm.
【分析】由BD是中线,可得AD=CD,又由△ABD的周长比△BCD的周长大6cm,△ABC的周长是21cm,AB=AC,可得AB-BC=6cm,2AB+BC=21cm,继而求得答案.
【详解】解:∵BD是中线,
∴AD=CD=AC,
∵△ABD的周长比△BCD的周长大6cm,
∴(AB+AD+BD)﹣(BD+CD+BC)=AB﹣BC=6cm①,
∵△ABC的周长是21cm,AB=AC,
∴2AB+BC=21cm②,
联立①②得:AB=9cm,BC=3cm.
【点睛】本题考查了三角形周长与三角形的中线.注意掌握数形结合思想与方程思想的应用.
题型十:三角形中线有关求面积问题
1.(2021·广东八年级期末)如图,中,、分别是、的中点,若的面积是10,则的面积是( )
A. B. C.5 D.10
【答案】B
【分析】根据三角形的中线把三角形分成面积相等的两部分,求出面积比,即可求出△ABE的面积.
【详解】∵AD是BC上的中线,
∴ S△ABD=S△ACD=S△ABC ,
∵BE是△ABD中AD边上的中线,
∴ S△ABE=S△BED=S△ABD ,
∴ S△ABE=SΔABC ,
∵△ABC的面积是10,
∴ S△ABE=×10=.
故选:B.
【点睛】本题考查的是三角形的中线的性质,三角形一边上的中线把原三角形分成的两个三角形的面积相等.
2.(2020·湛江市第二十二中学八年级月考)如图,已知∠BDC+∠EFC=180°,∠DEF=∠B.
(1)求证:ED∥BC;
(2)若D,E,F分别是AB,AC,CD边上的中点,四边形ADFE的面积为6.
①求△ABC的面积;
②若G是BC边上一点,CG=2BG,求△FCG的面积.
【答案】(1)证明见解析;(2)①16;②
【分析】(1)根据同角的补角线段得出∠BDC=∠EFD,即可证得AB∥EF,根据平行线的性质得出∠ADE=∠DEF,即可得出∠B=∠ADE,从而证得结论;
(2)根据三角形的中线把三角形分成面积相等的两个三角形进行计算即可.
(3)连接DG,由CG=2BG,得到S△DCG=2S△DBG,即可得到,进一步得到.
【详解】解:(1)如图,∵∠BDC+∠EFC=180°,∠EFD+∠EFC=180°,
∴∠BDC=∠EFD,
∴AB∥EF,
∴∠ADE=∠DEF,
又∵∠B=∠DEF,
∴∠B=∠ADE,
∴ED∥BC;
(2)设△CEF的面积为a,
∵F是CD的中点,
∴S△DEF=a,
∴S△CDE=2a,
同理,S△ADC=4a,S△ABC=8a,
∴S四边形ADFE=3a,
∵四边形ADFE的面积为6.
∴3a=6,即a=2,
∴S△ABC=8a=16;
(3)如图,连接DG,
∵CG=2BG,
∴S△DCG=2S△DBG,
∴,
∵F是CD的中点,
∴.
【点睛】本题考查了行线的判定与性质,三角形的面积,明确三角形的中线把三角形分成面积相等的两个三角形是解题的关键.
考点六:三角形重心
题型十一:重心的概念及有关应用
一、单选题
1.(2022·全国·八年级专题练习)如图所示的网格由边长相同的小正方形组成,点A、B、C、D、E、F、G在小正方形的顶点上,则△ABC的重心是( )
A.点D B.点E C.点F D.点G
【答案】A
【分析】根据重心的定义:三角形中各边中线的交点为三角形的重心,结合图形,可知D点为△ABC的重心.
【详解】如图所示,根据图形可知AN=BN,BM=CM,
∴AM,CN为△ABC的中线,
∵AM,CN交于点D,
∴D点为△ABC的重心.
故选:A.
【点睛】本题主要考查的是三角形重心的定义,属于基础题型.
2.(2022·湖南益阳·八年级期末)如图,等边三角形ABC中,AD⊥BC于D,BE平分∠ABC交AD、AC于点O、E, ABC的重心是( )
A.点D B.点E C.点O D.不能确定
【答案】C
【分析】根据等边三角形的性质以及三角形重心的定义可知,三角形中线的交点是三角形的重心,据此即可求解.
【详解】解:等边三角形ABC中,AD⊥BC于D,BE平分∠ABC交AD、AC于点O、E,
是等边的中线,
点是 ABC的重心
故选C
【点睛】本题考查了三角形重心的定义,掌握三角形的重心是三角形三条中线的交点是解题的关键.
二、填空题
3.(2022·全国·八年级专题练习)三角形的中线把三角形分成了面积相等的两部分,而三条中线交于一点,这一点叫此三角形的_________心.
【答案】重
【分析】根据三角形的重心的定义即可求解.
【详解】三角形的三条中线交于一点,这一点叫此三角形的重心;
故答案为:重.
【点睛】本题主要考查了三角形的重心,重心是三角形三边中线的交点;三角形的中线将三角形的面积分成了相等的两部分,重心到顶点的距离与重心到对边中点的距离之比为.
考点七:三角形的角平分线
题型十二:三角形角平分线定义
1.(2020·深圳市龙岗区百合外国语学校七年级期中)下列叙述正确的是( )
①三角形的中线、角平分线都是射线;②三角形的中线将三角形分成面积相等的两个小三角形;③三角形的三条高交于一点;④三角形的三条角平分线交于一点.
A.②④ B.①②④ C.③④ D.④
【答案】A
【分析】分别根据三角形中线、角平分线和高线的定义判断即可.
【详解】解:①三角形的中线、角平分线都是线段,原说法错误;
②三角形的中线将三角形分成面积相等的两个小三角形,说法正确;
③三角形的三条高所在直线交于一点,原说法错误;
④三角形的三条角平分线交于一点,说法正确.
故选:A.
【点睛】本题考查了三角形的面积,三角形的角平分线、中线和高,熟记定义即可作出正确的判断,属于基础题.
2.(2020·珠海市紫荆中学八年级期中)如图,在中,是高,是中线,是角平分线,交于点,交于点,下面说法①的面积的面积;②;③;④正确的是( )
A.①②③④ B.①②③ C.①②④ D.③④
【答案】B
【分析】根据等底等高的三角形的面积相等即可判断①;根据三角形内角和定理求出∠ABC=∠CAD,根据三角形的外角性质即可推出②;根据三角形内角和定理求出∠FAG=∠ACD,根据角平分线定义即可判断③;根据三角形的面积公式即可得到AD=4.8判断④.
【详解】解:∵BE是中线,
∴AE=CE,
∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故①正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故②正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故③正确;
∵∠BAC=90°,AD是高,
∴S△ABC=AB•AC=AD•BC,
∵AB=6,AC=8,BC=10,
∴AD==4.8,故④错误,
故选:
【点睛】本题考查了三角形内角和定理,三角形的外角性质,三角形的角平分线、中线、高,等腰三角形的判定等知识点,能综合运用定理进行推理是解此题的关键,题目比较好,属于中考题型.
3.(2019·广东八年级期中)如图,在△ABC中,∠BAC=90°,∠B=50°,AE,CF是角平分线,它们相交于为O,AD是高,求∠BAD和∠AOC的度数.
【答案】∠BAD=40°,∠AOC=115°.
【分析】先根据直角三角形的两个锐角互余,求得再根据角平分线的定义,求得最后根据三角形内角和定理,求得中的度数.
【详解】∵AD是高,
中,
∴△ABC中,
∵AE,CF是角平分线,
∴△AOC中,
考点八:三角形的稳定性
题型十三:三角形的稳定性
一、单选题
1.(2022·重庆巴蜀中学七年级期末)下列生活中的实例利用到三角形的稳定性的是( )
A.自行车的三角车架 B.用两颗钉子把木条固定在墙上
C.学校大门口的伸缩门 D.四条腿的方桌
【答案】A
【分析】分别利用三角形的稳定性和四边形的不稳定性等知识进行判断即可.
【详解】A、自行车的三角车架是利用了三角形的稳定性,符合题意;
B、用两颗钉子把木条固定在墙上是利用了两点确定一条直线,不符合题意;
C、学校大门口的伸缩门利用了四边形的不稳定性,不符合题意;
D、四条腿的方桌不是利用了三角形的稳定性,不符合题意.
故选:A.
【点睛】考查了三角形的稳定性,解题的关键是了解三角形具有稳定性和四边形具有不稳定性,难度不大.
2.(2022·黑龙江哈尔滨·七年级期末)下列图形中具有稳定性的是( ).
A.三角形 B.长方形 C.正方形 D.平行四边形
【答案】A
【分析】根据三角形具有稳定性,四边形具有不稳定性进行判断.
【详解】解:三角形具有稳定性.
故选:A.
【点睛】此题考查了三角形的稳定性和四边形的不稳定性.
二、填空题
3.(2022·陕西渭南·八年级期末)如图所示的手机支架.把手机放在上面就可以方便地使用手机,这是利用了三角形的___________.
【答案】稳定性
【分析】利用三角形的稳定性的性质直接回答即可.
【详解】解:把手机放在上面就可以方便地使用手机,这是利用了三角形的稳定性,
故答案为:稳定性.
【点睛】本题考查了三角形的稳定性,解题的关键是掌握三角形具有稳定性.
巩固提升
一.选择题(共10小题)
1.(2021秋•阳新县期末)如图表示的是三角形的分类,则正确的表示是( )
A.M表示三边均不相等的三角形,N表示等腰三角形,P表示等边三角形
B.M表示三边均不相等的三角形,N表示等边三角形,P表示等腰三角形
C.M表示等腰三角形,N表示等边三角形,P表示三边均不相等的三角形
D.M表示等边三角形,N表示等腰三角形,P表示三边均不相等的三角形
【分析】根据三角形按边的分类可直接选出答案.
【解答】解:三角形根据边分类如下:
三角形;
故选:B.
【点评】此题主要考查了三角形的分类,关键是掌握分类方法.三角形按边的关系分为两类:不等边三角形和等腰三角形,其中等腰三角形又分为底和腰不等的等腰三角形以及等边三角形.另外,三角形还可以按角进行分类.
2.(2021秋•松桃县期末)人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间线段最短 B.三角形的稳定性
C.两点确定一条直线 D.垂线段最短
【分析】根据三角形的稳定性解答即可.
【解答】解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:B.
【点评】此题考查了三角形的性质,关键是根据三角形的稳定性解答.
3.(2022春•昭通期末)下列说法中正确的是( )
A.三角形的三条中线必交于一点
B.直角三角形只有一条高
C.三角形的中线可能在三角形的外部
D.三角形的高线都在三角形的内部
【分析】根据三角形的高和中线的定义判断即可.
【解答】解:A、三角形的三条中线必交于一点,本选项说法正确,符合题意;
B、直角三角形有三条高,故本选项说法错误,不符合题意;
C、三角形的中线不可能在三角形的外部,故本选项说法错误,不符合题意;
D、三角形的高线不一定都在三角形的内部,故本选项说法错误,不符合题意;
故选:A.
【点评】本题考查的是三角形的高和中线,掌握它们的定义是解题的关键.
4.(2021秋•藁城区期末)如图,在△ABC中,AB=20,AC=18,AD为中线.则△ABD与△ACD的周长之差为( )
A.1 B.2 C.3 D.4
【分析】根据三角形的周长的计算方法得到△ABD的周长和△ADC的周长的差就是AB与AC的差.
【解答】解:∵AD是△ABC中BC边上的中线,
∴BD=DC=BC,
∴△ABD与△ACD的周长之差
=(AB+BD+AD)﹣(AC+DC+AD)
=AB﹣AC
=20﹣18
=2.
则△ABD与△ACD的周长之差=2.
故选:B.
【点评】本题考查三角形的中线的定义:三角形一边的中点与此边所对顶点的连线叫做三角形的中线,同时考查了三角形周长的计算方法.
5.(2021秋•天津期末)如图,在△ABC中,∠ACB=90°,CD⊥AB于D,图中线段中可以作为△ABC的高有( )
A.2条 B.3条 C.4条 D.5条
【分析】根据三角形的高的概念判断即可.
【解答】解:△ABC的高有AC、BC、CD共三条,
故选:B.
【点评】本题考查的是三角形的高的概念,从三角形的一个顶点向对边作垂线,垂足与顶点之间的线段叫做三角形的高.
6.(2021秋•两江新区期末)如图,在△ABC中,AB=5,AC=3,AD为BC边上的中线,则△ABD与△ACD的周长之差为( )
A.2 B.3 C.4 D.5
【分析】根据题意,AD是△ABC的边BC上的中线,可得BD=CD,进而得出△ABD的周长=AB+BD+AD,△ACD的周长=AC+CD+AD,相减即可得到周长差.
【解答】解:∵AD是△ABC的中线,
∴BD=CD,
∴△ABD与△ACD的周长之差为:(AB+BD+AD)﹣(AC+CD+AD)=AB+BD+AD﹣AC﹣CD﹣AD=AB﹣AC=5﹣3=2;
故选:A.
【点评】本题主要考查了三角形的中线、高和三角形周长的求法,熟练掌握三角形周长公式是解题的关键.
7.(2022•南通)用一根小木棒与两根长分别为3cm,6cm的小木棒组成三角形,则这根小木棒的长度可以为( )
A.1cm B.2cm C.3cm D.4cm
【分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边;即可求第三根木条的取值范围.
【解答】解:设第三根木条长为xcm,由三角形三边关系定理得6﹣3<x<6+3,即3<x<9,
即x的取值范围是3<x<9,观察选项,只有选项D符合题意.
故选:D.
【点评】本题主要考查了三角形三边关系,实际上就是根据三角形三边关系定理列出不等式,然后解不等式,确定取值范围即可,难度适中.
8.(2022春•耒阳市期末)下列各组线段能组成一个三角形的是( )
A.15cm,10cm,7cm B.4cm,5cm,10cm
C.2cm,2cm,4cm D.3cm,6cm,9cm
【分析】三角形的三条边必须满足:任意两边之和>第三边,任意两边之差<第三边.
【解答】解:A.7+10=17>15,能组成三角形,符合题意;
B.5+4=9<10,不能组成三角形,不符合题意;
C.2+2=4,不能组成三角形,不符合题意;
D.6+3=9,不能组成三角形,不符合题意.
故选:A.
【点评】本题主要考查对三角形三边关系的理解应用,判断是否可以构成三角形,只要判断两个较小的数的和>最大的数就可以.
9.(2022春•湖里区校级期末)下列各组能围成一个三角形的是( )
A.1,1,2 B.2,3,4 C.1,3,5 D.3,5,9
【分析】根据三角形的三边关系判断即可.
【解答】解:A、∵1+1=2,
∴长为1,1,2的三条线段不能组成三角形,本选项不符合题意;
B、∵3﹣2<4<3+2,
∴长为2,3,4的三条线段能组成三角形,本选项符合题意;
C、∵1+3=5,
∴长为1,3,5的三条线段不能组成三角形,本选项不符合题意;
D、∵3+5<9,
∴长为3,5,9的三条线段不能组成三角形,本选项不符合题意;
故选:B.
【点评】本题考查的是三角形的三边关系,熟记三角形两边之和大于第三边、三角形的两边差小于第三边是解题的关键.
10.(2022春•沙坪坝区校级期末)下列对△ABC的判断,错误的是( )
A.若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
B.若∠A=30°,∠B=50°,则△ABC是锐角三角形
C.若AB=AC,∠B=40°,则△ABC是钝角三角形
D.若2∠A=2∠B=∠C,则△ABC是等腰直角三角形
【分析】根据等腰三角形,等边三角形,直角三角形的判定以及三角形的内角和定理即可作出判断.
【解答】解:A.若∠A:∠B:∠C=1:2:3,则∠A=30°,∠B=60°,∠C=90°,所以△ABC是直角三角形,故此选项判断正确,不符合题意;
B.若∠A=30°,∠B=50°,则∠C=100°,所以△ABC是钝角三角形,故此选项判断不正确,符合题意;
C.若AB=AC,∠B=40°,则∠B=∠C=40°,∠A=100°,所以△ABC是钝角三角形,故此选项判断正确,不符合题意;
D.若2∠A=2∠B=∠C,则∠A=∠B=45°,∠C=90°,所以△ABC是直角三角形,故此选项判断正确,不符合题意.
故选:B.
【点评】本题考查了等边三角形的判定,直角三角形的判定,等腰三角形的判定和性质,三角形内角和定理等知识点,能熟记等腰三角形的性质和判定定理是解此题的关键.
二.填空题(共10小题)
11.(2021秋•岚皋县校级月考)图中以AE为边的三角形共有 3 个.
【分析】根据三角形的定义得出三角形的个数即可.
【解答】解;图中以AE为边的三角形有△AEC,△AED,△AEB共3个.
故答案为:3.
【点评】此题主要考查了三角形,正确把握三角形的定义是解题关键.
12.(2022春•灌云县期末)在△ABC中,AB<AC,BC边上的中线AD将△ABC分成的两个新三角形的周长差为5cm,AB与AC的和为13cm,则AC的长为 9cm .
【分析】关键三角形的中线的概念得到BD=CD,再根据三角形的周长公式、结合题意计算即可.
【解答】解:∵AD是△ABC的中线,
∴BD=CD,
∵AB<AC,两个新三角形的周长差为5cm,
∴(AC+AD+CD)﹣(AB+AD+BD)=5cm,
∴AC﹣AB=5cm,
∵AB+AC=13cm,
∴AC=9cm,
故答案为:9cm.
【点评】本题考查的是三角形的中线的概念,三角形一边的中点与此边所对顶点的连线叫做三角形的中线.
13.(2022春•辽阳期末)如图,∠D=∠E=∠FAC=90°,则线段 BD 是△ABC中AC边上的高.
【分析】根据过三角形的一个顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答.
【解答】解:∵∠D=90°,
∴BD⊥CD,
∴△ABC中AC边上的高是线段BD.
故答案为:BD.
【点评】本题考查了三角形的角平分线、中线和高,是基础题,熟记三角形的高的概念是解题的关键.
14.(2022春•清江浦区期末)三角形任意两边的和都 大 于第三边.
【分析】根据三角形的三边关系判断即可.
【解答】解:三角形任意两边的和都大于第三边,
故答案为:大.
【点评】本题考查的是三角形的三边关系,熟记三角形任意两边的和都大于第三边是解题的关键.
15.(2021秋•海珠区期末)如图,Rt△ABC中,∠C=90°,D是BC的中点,∠CAD=30°,BC=6,则AD+DB的长为 9 .
【分析】先根据D是BC的中点得出CD=DB=BC=3,然后根据30°角所对的直角边等于斜边的一半得出AD=2CD=6,进而求出AD+DB的长.
【解答】解:∵D是BC的中点,BC=6,
∴CD=DB=BC=3.
∵Rt△ABC中,∠C=90°,∠CAD=30°,
∴AD=2CD=6,
∴AD+DB=6+3=9.
故答案为:9.
【点评】本题考查了三角形的中线:三角形一边的中点与此边所对顶点的连线叫做三角形的中线.也考查了含30°角的直角三角形的性质,求出DB与AD是解题的关键.
16.(2020秋•饶平县校级期末)观察图形规律:
(1)图①中一共有 3 个三角形,图②中共有 6 个三角形,图③中共有 10 个三角形.
(2)由以上规律进行猜想,第n个图形共有 个三角形.
【分析】(1)根据图形直接数出三角形个数即可;
(2)根据(1)中所求得出数字变化规律,进而求出即可.
【解答】解:(1)如图所示:图①中一共有3个三角形,图②中共有6个三角形,图③中共有10个三角形.
故答案为:3,6,10;
(2)∵1+2=3,1+2+3=6,1+2+3+4=10,
∴第n个图形共有:1+2+3+…+(n+1)=.
故答案为:.
【点评】此题主要考查了数字变化规律,根据已知得出数字是连续整数的和是解题关键.
17.(2022春•江都区期末)一个三角形的周长为10cm,其中两边长分别是xcm、(2x﹣1)cm,则x的取值范围是 2<x<3 .
【分析】根据三角形的三边关系定理可得不等式组,再解不等式组即可求解.
【解答】解:由题意得,
解得:2<x<3.
故答案为:2<x<3.
【点评】此题主要考查了三角形的三边关系,以及一元一次不等式组的解法,关键是掌握三角形任意两边之和大于第三边,两边之差小于第三边.
18.(2022春•阜新县期末)已知一个三角形的两边长分别是2cm和4cm,第三边长x是奇数,则x的值是 3cm或5cm .
【分析】根据三角形的三边关系求得第三边的取值范围,再根据第三边是奇数求得第三边的长.
【解答】解:设第三边长x.
根据三角形的三边关系,得4﹣2<x<4+2.
即2<x<6,
又∵三角形的第三边长是奇数,
∴满足条件的数是3cm或5cm.
故答案为:3cm或5cm.
【点评】本题主要考查三角形三边关系的知识点,此题比较简单,注意三角形的三边关系,还要注意奇数这一条件.
19.(2022春•冠县期末)如图所示的自行车架设计成三角形,这样做的依据是三角形具有 稳定性 .
【分析】根据三角形具有稳定性解答.
【解答】解:自行车的主框架采用了三角形结构,这样设计的依据是三角形具稳定性,
故答案为:稳定性.
【点评】本题考查的是三角形的性质,掌握三角形具有稳定性是解题的关键.
20.(2020秋•齐河县期末)如图,共有 6 个三角形.
【分析】根据三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形数出三角形的个数.
【解答】解:图中有:△OAB,△OAC,△OAD,△OBC,△OCD,△OBD,共6个.
故答案为:6.
【点评】此题主要考查了三角形,关键是掌握三角形的定义,数三角形时,要不重不漏.
三.解答题(共7小题)
21.(2021秋•威县期末)在△ABC中,BC=8,AB=1;
(1)若AC是整数,求AC的长;
(2)已知BD是△ABC的中线,若△ABD的周长为10,求△BCD的周长.
【分析】(1)根据三角形的三边关系解答即可;
(2)根据三角形的中线的定义得到AD=CD,根据三角形的周长公式计算,得到答案.
【解答】解:(1)由题意得:BC﹣AB<AC<BC+AB,
∴7<AC<9,
∵AC是整数,
∴AC=8;
(2)∵BD是△ABC的中线,
∴AD=CD,
∵△ABD的周长为10,
∴AB+AD+BD=10,
∵AB=1,
∴AD+BD=9,
∴△BCD的周长=BC+BD+CD=BC+AD+CD=8+9=17.
【点评】本题考查的是三角形的三边关系、三角形的中线的定义,掌握三角形两边之和大于第三边、两边之差小于第三边是解题的关键.
22.(2022春•浚县校级期末)若一个三角形的三边长分别是a,b,c,其中a和b满足方程,若这个三角形的周长为整数,求这个三角形的周长.
【分析】利用加减消元法解出方程组,求出a、b,根据三角形的三边关系求出c,根据三角形的周长公式计算,得到答案.
【解答】解:解方程组,得,
则4﹣1<c<4+1,即3<c<5,
∵周长为整数,
∴c=4,
∴三角形的周长=4+4+1=9.
【点评】本题考查的是三角形的三边关系、二元一次方程组的解法,熟记三角形两边之和大于第三边、三角形的两边差小于第三边是解题的关键.
23.(2022春•榆树市期末)如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多1,AB与AC的和为11.
(1)求AB、AC的长;
(2)求BC边的取值范围.
【分析】(1)根据三角形中线的定义,BD=CD.所以△ABD和△ADC的周长之差也就是AB与AC的差,然后联立关于AB、AC的二元一次方程组,利用加减消元法求解即可.
(2)根据三角形三边关系解答即可.
【解答】解:(1)∵AD是BC边上的中线,
∴BD=CD,
∴△ABD的周长﹣△ADC的周长=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC=1,
即AB﹣AC=2①,
又AB+AC=11②,
①+②得.2AB=12,
解得AB=6,
②﹣①得,2AC=10,
解得AC=5,
∴AB和AC的长分别为:AB=6,AC=5;
(2)∵AB=6,AC=5,
∴1<BC<11.
【点评】本题考查了三角形的三边关系,三角形的中线定义,二元一次方程组的求解,利用加减消元法求解是解题的关键.
24.(2022春•曲阳县期末)某市木材市场上木棒规格与价格如下表:
规格
1m
2m
3m
4m
5m
6m
价格/(元/根)
10
15
20
25
30
35
小明的爷爷要做一个三角形的支架养鱼用,现有两根长度为3m和5m的木棒,还需要到该木材市场上购买一根.
(1)有几种规格的木棒可供小明的爷爷选择?
(2)在能做成三角形支架的情况下,选择哪一种规格的木棒最省钱?
【分析】(1)根据三角形的三边关系可得5﹣3<x<5+3,再解出不等式可得x的取值范围,进而得到选择的木棒长度;
(2)根据木棒价格可直接选出答案.
【解答】解:(1)设第三根木棒的长度为xm,
根据三角形的三边关系可得:5﹣3<x<5+3,
解得2<x<8,
x=3,4,5,6共4种,
∴有4种规格木棒可供小明的爷爷选择;
(2)根据木棒的价格可得选3m最省钱.
【点评】此题主要考查了三角形的三边关系,关键是掌握三角形三边关系定理:三角形两边之和大于第三边.三角形的两边差小于第三边.
25.(2020秋•东莞市校级期中)一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
【分析】题目给出等腰三角形有一条边长为6cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.
26.(2022春•神木市期末)如图,已知△ABC的周长为21cm,AB=6cm,BC边上的中线AD=5cm,△ABD的周长为15cm,求AC的长.
【分析】先根据△ABD周长为15cm,AB=6cm,AD=5cm,由周长的定义可求BD的长,再根据中线的定义可求BC的长,由△ABC的周长为21cm,即可求出AC长.
【解答】解:∵AB=6cm,AD=5cm,△ABD周长为15cm,
∴BD=15﹣AB﹣AD=15﹣6﹣5=4(cm),
∵AD是BC边上的中线,
∴BC=8cm,
∵△ABC的周长为21cm,
∴AC=21﹣AB﹣BC=21﹣6﹣8=7(cm).
故AC长为7cm.
【点评】考查了三角形的周长和中线,本题的关键是由周长和中线的定义得到BC的长,题目难度中等.
27.(2021秋•章贡区期中)如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
【分析】根据中线的定义知CD=BD.结合三角形周长公式知AC﹣AB=5cm;又AC+AB=13cm.易求AC的长度.
【解答】解:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长﹣△ABD的周长=5cm.
∴AC﹣AB=5cm.
又∵AB+AC=13cm,
∴AC=9cm.
即AC的长度是9cm.
【点评】本题考查了三角形的中线,根据周长的差表示出AC﹣AB=5cm,是解题的关键.
第11讲 乘法公式(4大考点)2022-2023学年八年级数学考试满分全攻略(人教版): 这是一份第11讲 乘法公式(4大考点)2022-2023学年八年级数学考试满分全攻略(人教版),文件包含第11讲乘法公式4大考点解析版docx、第11讲乘法公式4大考点原卷版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
第10讲 整式的乘法(7大考点)2022-2023学年八年级数学考试满分全攻略(人教版): 这是一份第10讲 整式的乘法(7大考点)2022-2023学年八年级数学考试满分全攻略(人教版),文件包含第10讲整式的乘法7大考点解析版docx、第10讲整式的乘法7大考点原卷版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
第07讲 轴对称、画轴对称图形(3大考点15种解题方法)2022-2023学年八年级数学考试满分全攻略(人教版): 这是一份第07讲 轴对称、画轴对称图形(3大考点15种解题方法)2022-2023学年八年级数学考试满分全攻略(人教版),文件包含第07讲轴对称画轴对称图形3大考点15种解题方法解析版docx、第07讲轴对称画轴对称图形3大考点15种解题方法原卷版docx等2份试卷配套教学资源,其中试卷共82页, 欢迎下载使用。












