数学八年级下册3 线段的垂直平分线教学演示ppt课件

课题

1.3.2　三角形三边的垂直平分线

授课人

CQY

教学目标

1.会证明三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等，并解决相关的问题．

2．会用尺规作已知线段的垂直平分线，培养尺规作图的技能．

教学重点

掌握三角形三条边的垂直平分线的性质，能利用尺规作出符合条件的三角形.

教学难点

三角形三条边的垂直平分线性质的证明及应用.

授课类型

新授课

课时

1课时

教学活动

教学步骤

师生活动

设计意图

环节一：

创设情境、导入新课

【课堂引入】

1. 问题提出：

利用尺规作三角形三条边的垂直平分线，当作图完成后你发现了什么？(教师可用多媒体演示作图过程)

2. 问题探究：

①三角形三边的垂直平分线交于一点；

②这一点到三角形三个顶点的距离相等．

3. 问题解决：

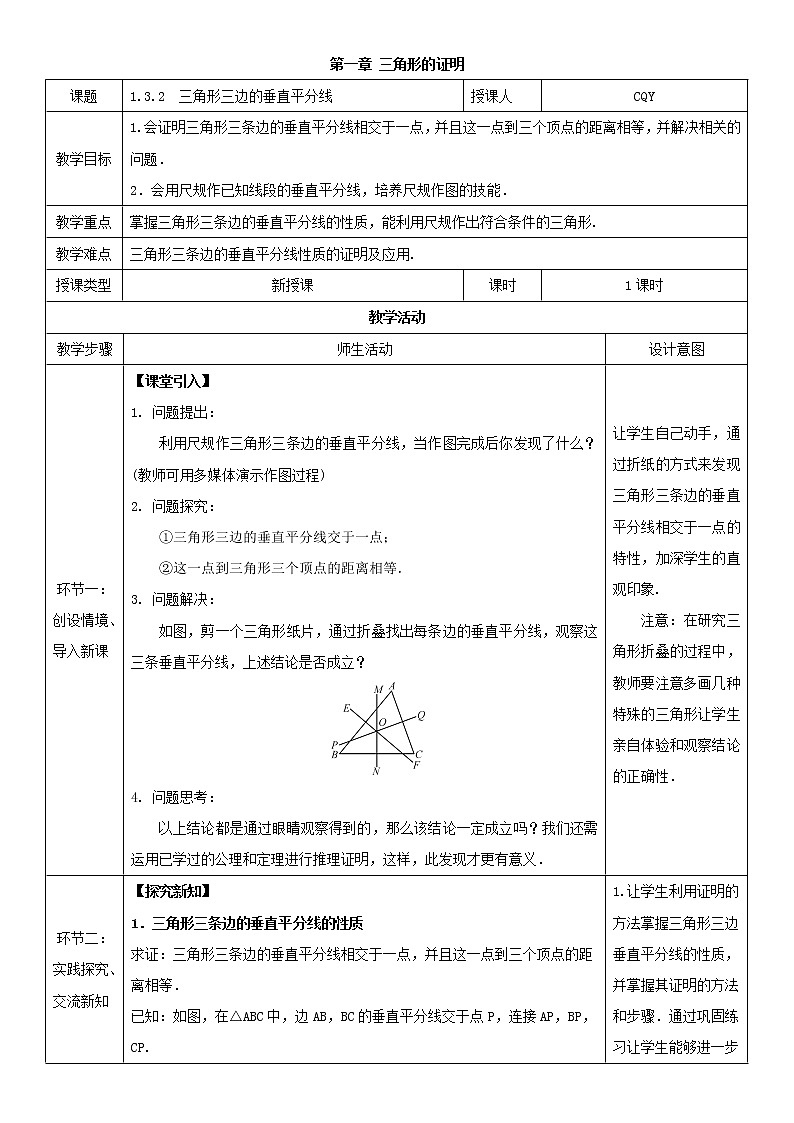
如图，剪一个三角形纸片，通过折叠找出每条边的垂直平分线，观察这三条垂直平分线，上述结论是否成立？

4. 问题思考：

以上结论都是通过眼睛观察得到的，那么该结论一定成立吗？我们还需运用已学过的公理和定理进行推理证明，这样，此发现才更有意义．

让学生自己动手，通过折纸的方式来发现三角形三条边的垂直平分线相交于一点的特性，加深学生的直观印象.

注意：在研究三角形折叠的过程中，教师要注意多画几种特殊的三角形让学生亲自体验和观察结论的正确性．

环节二：

实践探究、交流新知

【探究新知】

1．三角形三条边的垂直平分线的性质

求证：三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等．

已知：如图，在△ABC中，边AB，BC的垂直平分线交于点P，连接AP，BP，CP.

求证：边AC的垂直平分线经过点P，且PA＝PB＝PC.

证明：∵点P在线段AB的垂直平分线上，

∴PA＝PB(线段垂直平分线上的点到这条线段两个端点的距离相等)．

同理，PB＝PC.∴PA＝PB＝PC.

∴点P在线段AC的垂直平分线上(到一条线段两个端点距离相等的点，在这条线段的垂直平分线上)，

即边AC的垂直平分线经过点P.

2．已知等腰三角形的底边和该边上的高，求作等腰三角形．

(1)已知三角形的一条边及这条边上的高，你能作出三角形吗？如果能，能作几个？所作出的三角形都全等吗？

(2)已知等腰三角形的底边，你能用尺规作出等腰三角形吗？如果能，能作几个？所作出的三角形都全等吗？

(3)已知等腰三角形的底边及底边上的高，你能用尺规作出等腰三角形吗？如果能，能作几个？

解：(1)已知三角形的一条边及这条边上的高，能作出三角形，并且能作出无数多个，如图所示．

从上图我们会发现，先作已知线段BC＝a；然后再作BC边上的高h，但垂足不确定，我们可将垂足取在线段BC所在直线上的任意一点D，过此点作BC边的垂线，最后以D为端点在垂线上截取AD(或A1D)，使AD＝A1D＝h，连接AB，AC(或A1B，A1C)，所得△ABC(或△A1BC)都满足条件，所以这样的三角形有无数多个．这些三角形不都全等．

(2)已知等腰三角形的底边，用尺规作出等腰三角形，这样的等腰三角形也有无数多个．根据线段垂直平分线的性质定理可知，线段垂直平分线上的点到线段两个端点的距离相等，因此只要作已知等腰三角形底边的垂直平分线，取它上面的任意一点(与底边的交点除外，底边的中点在底边上，此时不能构成三角形)，和底边的两个端点相连接，都可以得到一个等腰三角形，如图所示．

(3)如果等腰三角形的底边和底边上的高都一定，这样的等腰三角形应该只有两个，它们是全等的，且分别位于已知底边的两侧，如图所示．

1.让学生利用证明的方法掌握三角形三边垂直平分线的性质，并掌握其证明的方法和步骤．通过巩固练习让学生能够进一步掌握线段垂直平分线的性质的应用．

2．让学生掌握如何在已知底边和高的情况下作一个等腰三角形，同时进一步使学生掌握线段垂直平分线的作法．

环节三：

开放训练、体现应用

【典型例题】　　

例1　如图，在△ABC中，AB的垂直平分线l1交AB于点M，交BC于点D，AC的垂直平分线l2交AC于点N，交BC于点E，l1与l2相交于点O，△ADE的周长为10.

(1)求BC的长；

(2)试判断点O是否在边BC的垂直平分线上，并说明理由．

解：(1)∵l1垂直平分AB，∴DB＝DA.

同理EA＝EC.

∴BC＝BD＋DE＋EC＝DA＋DE＋EA＝10.

(2)点O在边BC的垂直平分线上．

理由：连接AO，BO，CO，

∵l1，l2分别是线段AB，AC的垂直平分线，

∴AO＝BO，CO＝AO.∴BO＝CO.

∴点O在边BC的垂直平分线上．

例2　尺规作图：如图，已知线段a，求作△ABC，使AB＝AC，且BC＝a，高AD＝2a.

解：如图．①作射线BE，在射线BE上截取BC＝a.

②作BC的垂直平分线EF，交BC于点D.

③在EF上截取AD＝2a，连接AB，AC，则△ABC即为所求．

【变式训练】

如图，在△ABC中，∠BAC＝80°，若MP和NQ分别垂直平分AB和AC.

(1)求∠PAQ的度数；

(2)若△APQ的周长为12，BC的长为8，求PQ的长．

解：(1)设∠PAQ＝x°，∠CAP＝y°，∠BAQ＝z°，

∵MP和NQ分别垂直平分AB和AC，

∴AP＝PB，AQ＝CQ.

∴∠B＝∠BAP＝(x＋z)°，∠C＝∠CAQ＝(x＋y)°.

∵∠BAC＝80°，∴∠B＋∠C＝100°，

即x＋y＋z＝80，x＋z＋x＋y＝100.

∴x＝20.

∴∠PAQ＝20°.

(2)∵△APQ的周长为12，∴AQ＋PQ＋AP＝12.

∵AQ＝CQ，AP＝PB，∴CQ＋PQ＋PB＝12.

∴CQ＋BQ＋2PQ＝12，即BC＋2PQ＝12.

∵BC＝8，∴PQ＝2.

师生活动：学生独立思考，举手回答，师生交流心得和方法.

通过例题的解决，加深学生对本课知识的掌握，使学生进一步熟练掌握利用尺规作一条已知线段的垂直平分线.

环节四：

课堂检测、

巩固新知

【课堂检测】

1.某地兴建的幸福家园的三个出口A，B，C的位置如图所示，物业公司计划在不妨碍小区规划建设前提下，在小区内修建一个电动车充电桩，以方便业主，要求充电桩到三个出口的距离都相等，则充电桩应该安装在△ABC(A)

A．三条边的垂直平分线的交点  B．三个角的角平分线的交点

C．三角形三条高的交点  D．三角形三条中线的交点

第1题图                    第2题图

2．如图，线段AB，BC的垂直平分线l1，l2相交于点O.若∠AOC＝78°，则∠1的度数为39°．

3．如图，在△ABC中，∠BAC是钝角．

(1)画出边BC上的中线AD；

(2)画出边BC上的高AH.

解：(1)(2)如图所示．

针对本课时的重难点，分层次进行检测，达到学有所成、了解课堂学习效果的目的，并最大限度地调动全体学生学习数学的积极性，使每个学生都能有所收益、有所提高.

环节五：

课堂小结、

整体感知

1.课堂小结：

本节课你学到了什么知识？

1．三角形三条边的垂直平分线的性质

2. 尺规作线段的垂直平分线、等腰三角形

2．布置作业：

(1)教材第26页随堂练习．

(2)教材第26页习题1.8第1，2题.

锻炼学生的语言表达能力和归纳总结能力，巩固所学知识.

板书设计

教学反思