2023年高考数学二轮复习重点基础练习：专题六 三角函数 综合训练（C卷）

这是一份2023年高考数学二轮复习重点基础练习：专题六 三角函数 综合训练（C卷），共8页。试卷主要包含了已知，则，函数的最小值和最小正周期分别为，已知函数的部分图像如图所示，且等内容，欢迎下载使用。
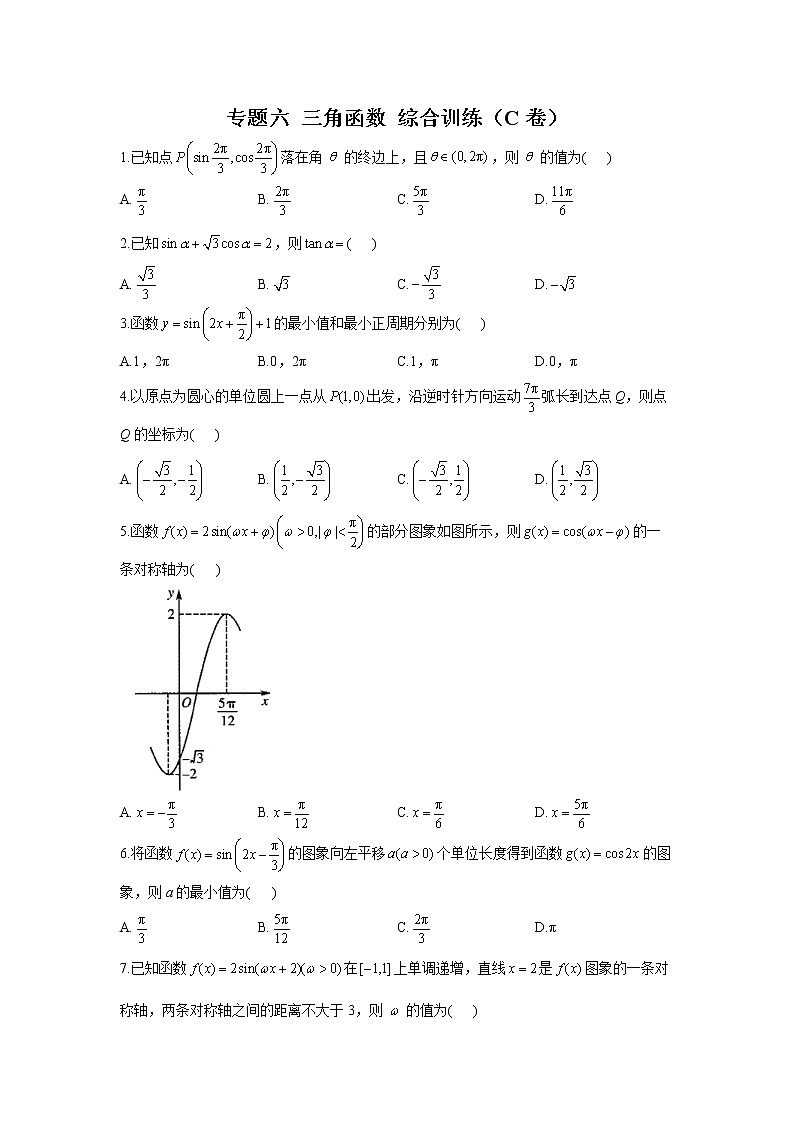
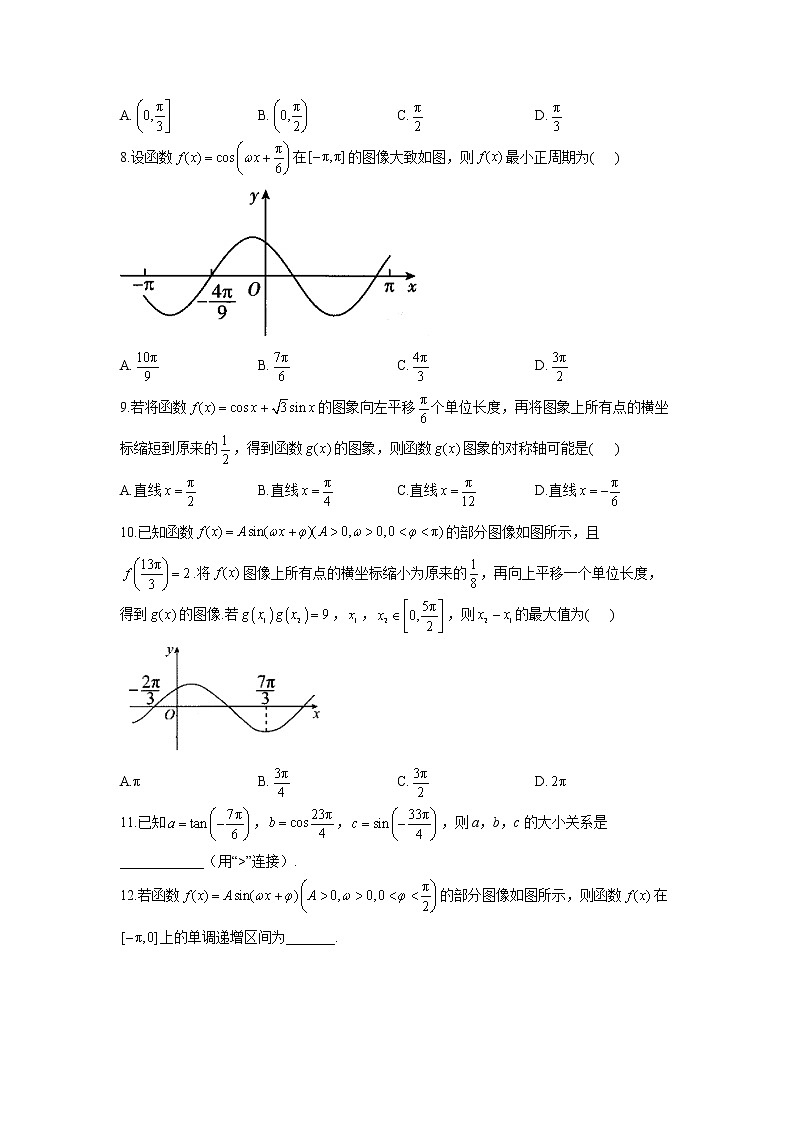
专题六 三角函数 综合训练（C卷）1.已知点落在角的终边上，且，则的值为(   )A. B. C. D.2.已知，则(   )A. B. C. D.3.函数的最小值和最小正周期分别为(   )A.1，2π B.0，2π C.1，π D.0，π4.以原点为圆心的单位圆上一点从出发，沿逆时针方向运动弧长到达点Q，则点Q的坐标为(   )A. B. C. D.5.函数的部分图象如图所示，则的一条对称轴为(   )A. B. C. D.6.将函数的图象向左平移个单位长度得到函数的图象，则a的最小值为(   )A. B. C. D.π7.已知函数在上单调递增，直线是图象的一条对称轴，两条对称轴之间的距离不大于3，则的值为(   )A. B. C. D.8.设函数在的图像大致如图，则最小正周期为(   )
 A. B. C. D.9.若将函数的图象向左平移个单位长度，再将图象上所有点的横坐标缩短到原来的，得到函数的图象，则函数图象的对称轴可能是(   )A.直线 B.直线 C.直线 D.直线10.已知函数的部分图像如图所示，且.将图像上所有点的横坐标缩小为原来的，再向上平移一个单位长度，得到的图像.若，，，则的最大值为(   )A.π B. C. D.11.已知，，，则a，b，c的大小关系是____________（用“>”连接）.12.若函数的部分图像如图所示，则函数在上的单调递增区间为_______.13.已知，且，则__________，____________.14.函数的图象与函数的图象在上所有交点的横坐标之和为______________.15.设函数，.（1）已知，函数是偶函数，求的值；（2）求函数的值域.
答案以及解析1.答案：D解析：由，知角是第四象限角.因为，，所以，故选D.2.答案：A解析：解法一  由得，得，则，所以，故选A.解法二  ，故，可得，，即，，所以，故选A.3.答案：D解析：当时，取得最小值，且.又其最小正周期，的最小值和最小正周期分别是0，π.故选D.4.答案：D解析：设单位圆的半径为r，圆弧的长为l，则，，对应的圆心角.设，由三角函数定义，可得，.点Q的坐标为.5.答案：D解析：由得，方程为.由图象可知，即，.令，则，令得是的一条对称轴，故选D.6.答案：B解析：将函数的图象向左平移个单位长度，可得函数的图象，所以的图象与的图象重合.因为，所以，，即，，当时，可得，故选B.7.答案：D解析：，在上单调递增，则的最小正周期.直线是图象的一条对称轴.区间的长度小于2，在上单调递增，则的最小正周期，.两条对称轴之间的距离不大于3，则的最小正周期，，，故选D.8.答案：C解析：由图像可得，所以，，则，.设函数的最小正周期为T，则，即所以.所以，，经验证可知，当时与题图相符.所以的最小正周期，故选C.9.答案：C解析：由题得，将的图象向左平移个单位长度，得到函数的图象，再将图象上所有点的横坐标缩短到原来的，得到函数的图象，令，得.当时，得函数图象的一条对称轴为直线.故选C.10.答案：D解析：设的最小正周期为T，则由题图可知，得，则，所以.又由题图可知图像的一个对称中心为点，故，，故，，因为，所以，所以.又因为，所以，所以.将图像上所有点的横坐标缩小为原来的，再向上平移一个单位长度，得到的图像.因为，所以，同时令取得最大值3.由，可得，.又，，要求的最大值，故令，得；令，得，所以的最大值为.故选D.11.答案：解析：，，，.12.答案：解析：由函数的部分图像，可得，，求得.再根据五点作图法可得，，，，.又，，.令，，解得，，故函数的增区间为，.再根据，可得增区间为.13.答案：；解析：由得，所以，所以.14.答案：7解析：令，得，，即，.由得在同一平面直角坐标系中分别作出函数，的大致图象，如图所示.易知函数与函数的图象均关于直线对称，因此这两个函数图象的交点关于直线对称.又，，所以，图象的其中一个交点在对称轴上，其余交点成对出现.结合图象知当时，除了对称轴上的交点外，两函数图象还有三对交点，因此所有交点的横坐标之和为.15.答案：（1）或（2）解析：（1）因为是偶函数，所以，对任意实数x都有，即，故，所以.又，因此或.（2）.因此，函数的值域是.