2023年高考数学二轮复习重点基础练习：专题六 三角函数 综合训练（A卷）

这是一份2023年高考数学二轮复习重点基础练习：专题六 三角函数 综合训练（A卷），共7页。试卷主要包含了若为第四象限角，则，若，，则，与函数的图象不相交的一条直线是，设函数，则下列结论正确的是，已知函数，则是，关于函数有下述四个结论等内容，欢迎下载使用。
专题六 三角函数 综合训练（A卷）1.已知角的顶点为坐标原点，始边与x轴的非负半轴重合，终边上有一点，则(   )A. B. C. D.2.若为第四象限角，则(   )A. B. C. D.3.若，，则(   )A. B. C. D.4.若将函数的图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，再向右平移个单位长度，则所得函数的图象的一个对称中心为(   )
A. B. C. D.5.与函数的图象不相交的一条直线是(   )
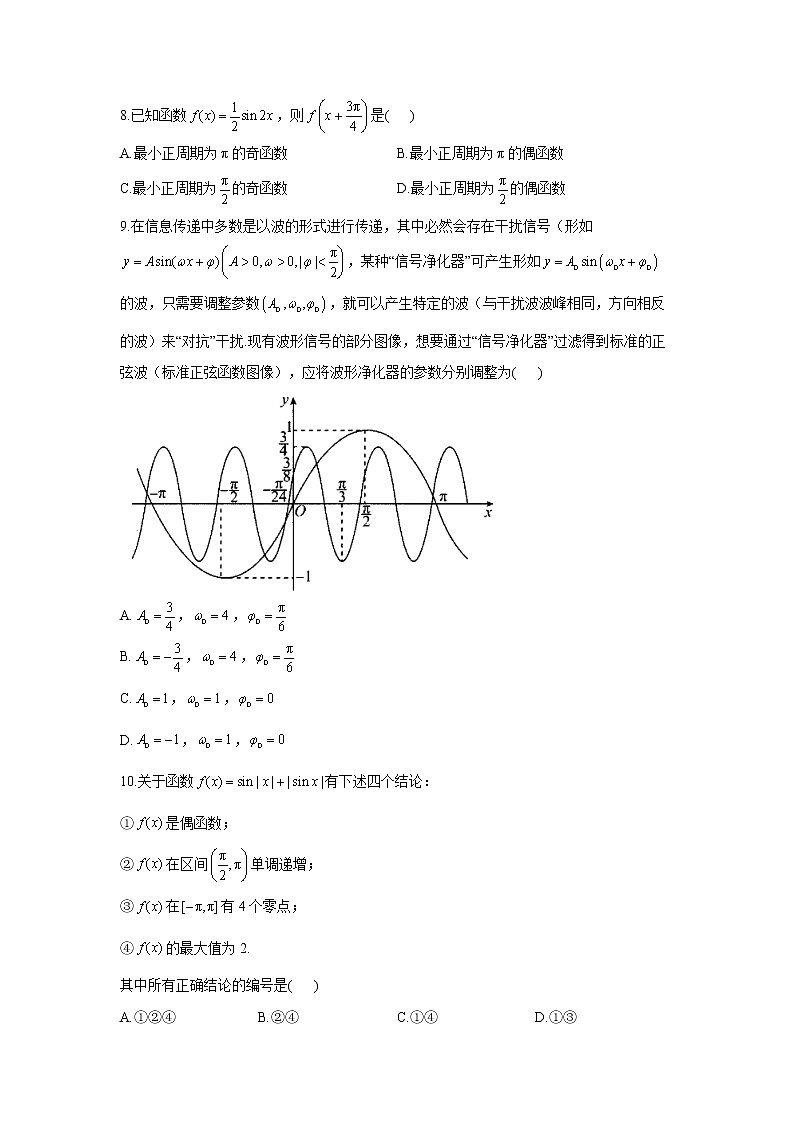
A. B. C. D.6.设函数，则下列结论正确的是(   )A.的一个周期为B.的图像关于直线对称C.的一个零点是D.在上单调递增7.已知把函数的图象向右平移个单位长度，可得函数的图象，则的最小正值为(   )A. B. C. D.8.已知函数，则是(   )A.最小正周期为π的奇函数 B.最小正周期为π的偶函数C.最小正周期为的奇函数 D.最小正周期为的偶函数9.在信息传递中多数是以波的形式进行传递，其中必然会存在干扰信号（形如，某种“信号净化器”可产生形如的波，只需要调整参数，就可以产生特定的波（与干扰波波峰相同，方向相反的波）来“对抗”干扰.现有波形信号的部分图像，想要通过“信号净化器”过滤得到标准的正弦波（标准正弦函数图像），应将波形净化器的参数分别调整为(   )A.，，B.，，C.，，D.，，10.关于函数有下述四个结论：①是偶函数；②在区间单调递增；③在有4个零点；④的最大值为2.其中所有正确结论的编号是(   )A.①②④ B.②④ C.①④ D.①③11.若函数的图象向右平移个单位长度后得到的图象，函数的零点到y轴的最近距离小于，且在上单调递增，则的取值范围为________.12.已知，，则___________.13.已知扇形的圆心角为120°，半径为cm，则此扇形的面积为____________cm².14.已知函数的部分图象如图所示，则_______，____________.15.已知函数图象上最高点的纵坐标为2，且图象上相邻两个最高点的距离为.(1)求和的值;(2)求函数在上的单调递减区间.
答案以及解析1.答案：A解析：易知，由三角函数定义得，即，得，解得或（舍去）.2.答案：D解析：是第四象限角，，，，，角的终边在第三、四象限或y轴非正半轴上，，可正、可负、可为零.故选D.3.答案：C解析：由，得，所以，则，故选C.4.答案：A解析：将的图象上各点的横坐标伸长到原来的2倍（纵坐标不变），可以得到的图象，
再向右平移个单位长度，可以得到的图象，
因此，，则，故选A.5.答案：C解析：由，，得，，
则当时，，
即直线与函数图象不相交.6.答案：B解析：本题考查余弦型函数的周期性、对称性、零点和单调性.由可知的最小正周期选项A错误；因为所以的图像关于直线对称，选项B正确，选项C错误；因为的最小正周期为所以在上不可能是单调的，选项D错误.故选B.7.答案：C解析：，，，即，解得，为最小正值，故选C.8.答案：B解析：，，，是最小正周期为π的偶函数，故选B.9.答案：B解析：本题考查三角函数图像的性质.设干扰信号对应的函数解析式为.由题图得（T为干扰信号的周期，解得，.函数的最大值为，.将代入，解得，，，..欲消除的波需要选择相反的波，即，故选B.10.答案：C解析：的定义域为，，故是偶函数，①正确；当时，，其在该区间上单调递减，②不正确；当时，，有两个零点，当时，仅有一个零点，所以在上有三个零点，故③不正确；当时，，其最大值为2，又是R上的偶函数，所以在R上的最大值为2，④正确.综上，①④正确，②③不正确.故选C.11.答案：解析：设的最小正周期为T，依题意为的一个零点，且，所以，所以在上有且只有一个零点，可得，化简得，故的取值范围为.12.答案：解析：由题知，，，.13.答案：解析：设扇形的弧长为lcm，半径为R cm，圆心角的弧度数为，
因为，
所以.
所以.14.答案：2；解析：由题图可知，，函数的最小正周期，所以，所以.易知，故，解得，所以，.15.答案：(1)2(2) 解析：(1)当时，取得最大值为.又图象上最高点的纵坐标为2，，即.又的图象上相邻两个最高点的距离为，的最小正周期，.(2)由(1)得，由，得.令，得.函数在上的单调递减区间为.