北师大版八年级下册4 角平分线授课ppt课件

这是一份北师大版八年级下册4 角平分线授课ppt课件，共22页。PPT课件主要包含了复习导入，亲爱的同学们，新知讲解，图1-22，想一想，图1-23，图1-24，课堂练习，中考链接，课堂总结等内容，欢迎下载使用。

还记得角平分线上的点有什么性质吗？
定理 角平分线上的点到这个角的两边的距离相等.
你是怎样得到的？请你尝试证明这一性质，并与同伴交流.
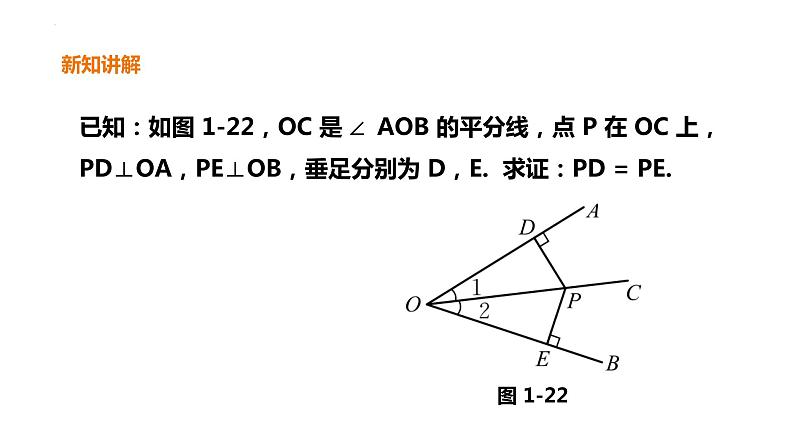
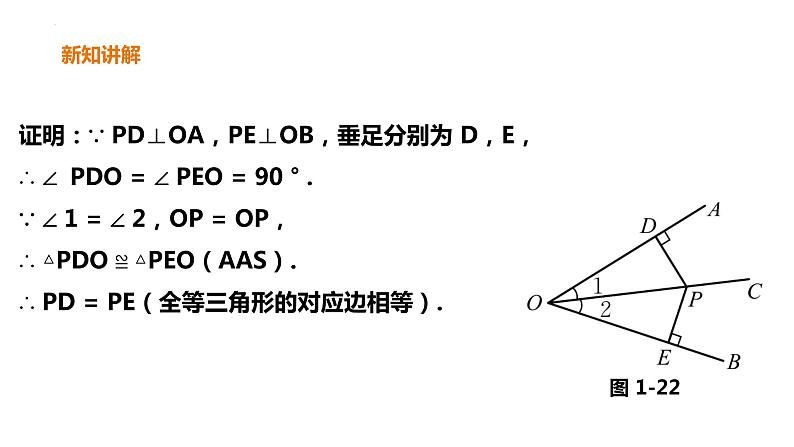
已知：如图 1-22，OC 是 ∠ AOB 的平分线，点 P 在 OC 上，PD⊥OA，PE⊥OB，垂足分别为 D，E. 求证：PD = PE.
证明：∵ PD⊥OA，PE⊥OB，垂足分别为 D，E，∴ ∠ PDO = ∠ PEO = 90 ° .∵ ∠ 1 = ∠ 2，OP = OP，∴ △PDO ≌ △PEO（AAS）.∴ PD = PE（全等三角形的对应边相等）.
你能写出这个定理的逆命题吗？它是真命题吗？
定理 在一个角的内部，到角的两边距离相等的点在这个角的平分线上.
已知：如图 1-23，点 P 为 ∠ AOB 内一点，PD⊥OA，PE⊥OB，垂足分别为 D，E，且 PD = PE.求证：OP 平分 ∠ AOB.
证明：∵ PD⊥OA，PE⊥OB，垂足分别为 D，E∴ ∠ ODP = ∠ OEP = 90 ° .∵ PD = PE，OP = OP，∴ Rt△DOP ≌ Rt△EOP（HL）.∴ ∠ 1 = ∠ 2（全等三角形的对应角相等）.∴ OP 平分 ∠ AOB.
如图 1-24，在 △ABC 中，∠ BAC = 60 ° ，点 D 在 BC 上，AD = 10，DE⊥AB，DF⊥AC，垂足分别为 E，F，且 DE = DF，求 DE 的长.
解：∵ DE⊥AB，DF⊥AC，垂足分别为 E，F， 且 DE = DF，∴ AD 平分 ∠ BAC（在一个角的内部，到角的两边距离相等的点在这个角的平分线上）.又∵ ∠ BAC = 60 ° ，∴ ∠ BAD = 30 ° .在 Rt△ADE 中，∠ AED = 90 ° ，AD = 10，∴ DE= AD = × 10 = 5（在直角三角形中，如果一个锐角等于30 ° ，那么它所对的直角边等于斜边的一半）.
1、如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，连接EF交AD于G.下列结论：①AD垂直平分EF；②EF垂直平分AD；③AD平分∠EDF；④当∠BAC为60°时，AG=3DG，其中不正确的结论的个数为( )A. 1B. 2C. 3D. 4
解：∵AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，∴DE=DF，∠AED=∠AFD=90°，在Rt△AED和Rt△AFD中， AD=AD DE=DF ，∴Rt△AED≌Rt△AFD(HL)，∴AE=AF，∠ADE=∠ADF，∴AD平分∠EDF；③正确；
∵AD平分∠BAC，AE=AF，DE=DF，∴AD垂直平分EF，①正确；②错误，∵∠BAC=60°，∴∠DAB=30°，∴AG= AE，AD= AE，∴DG= AE，∴AG=3DG，④正确． 故选A．
2、如图：△ABC中，DE是BC边的垂直平分线，垂足为E，AD平分∠BAC且MD⊥AB，DN⊥AC延长线于N.求证：BM=CN．
证明：连接BD，DC，如图：∵DE所在直线是BC的垂直平分线，∴BD=CD，∵AD平分∠BAC，过点D作DM⊥AB于点M，DN⊥AC交AC的延长线于点N，∴DM=DN，在Rt△BMD与Rt△CDN中，DM=DN BD=DC，∴Rt△BMD≌Rt△CDN(HL)，∴BM=CN
已知∠MAN=120°，AC平分∠MAN，点B、D分别在AN、AM上(1)如图1，若∠ABC=∠ADC=90°，请你探索线段AD、AB、AC之间的数量关系，并证明之；(2)如图2，若∠ABC+∠ADC=180°，则(1)中的结论是否仍然成立？若成立，给出证明；若不成立，请说明理由．
(1)关系是：AD+AB=AC证明：∵AC平分∠MAN，∠MAN=120°∴∠CAD=∠CAB=60°又∠ADC=∠ABC=90°，∴∠ACD=∠ACB=30°则AD=AB= AC(直角三角形一锐角为30°，则它所对直角边为斜边一半)∴AD+AB=AC；
(2)仍成立．证明：过点C分别作AM、AN的垂线，垂足分别为E、F∵AC平分∠MAN∴CE=CF(角平分线上点到角两边距离相等)∵∠ABC+∠ADC=180°，∠ADC+∠CDE=180°∴∠CDE=∠ABC又∠CED=∠CFB=90°，∴△CED≌△CFB(AAS)∵ED=FB，∴AD+AB=AE-ED+AF+FB=AE+AF由(1)知AE+AF=AC ∴AD+AB=AC