初中数学北师大版八年级下册第一章 三角形的证明4 角平分线备课课件ppt

这是一份初中数学北师大版八年级下册第一章 三角形的证明4 角平分线备课课件ppt，文件包含141角平分线的性质与判定pptx、14角平分线第1课时角平分线的性质定理及逆定理doc等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

1 要求大家掌握角平分线的性质定理和逆定理，会用这两个定理解决一些简单问题.2 理解角平分线的性质定理和逆定理的证明.3 进一步发展大家的推理证明意识和能力.
1 什么叫角平分线？
如果一条射线把一个角分成两个相等的角，那么这条射线叫角的平分线.
2 还记得角平分线上的点有什么性质吗? 你是怎样得到的?
角平分线上的点到角两边的距离相等.
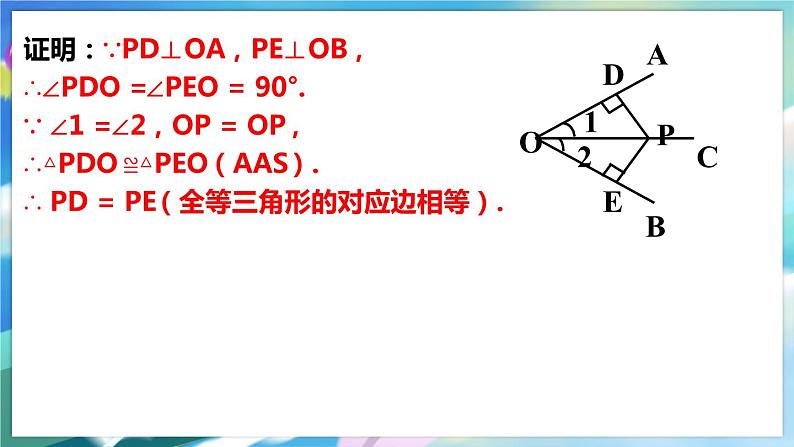
角平分线上的点到角两边的距离相等。已知：如图，OC是∠AOB的平分线，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D、E． 求证：PD=PE．
证明：∵PD⊥OA，PE⊥OB，∴∠PDO =∠PEO = 90°.∵ ∠1 =∠2，OP = OP，∴△PDO ≌△PEO（AAS）.∴ PD = PE（全等三角形的对应边相等）.
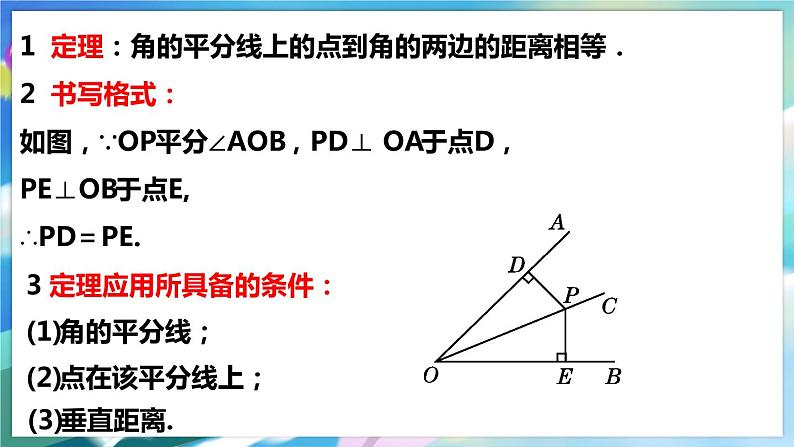
1 定理：角的平分线上的点到角的两边的距离相等．2 书写格式：如图，∵OP平分∠AOB，PD⊥ OA于点D，PE⊥OB于点E, ∴PD＝PE.
3 定理应用所具备的条件：
(2)点在该平分线上；
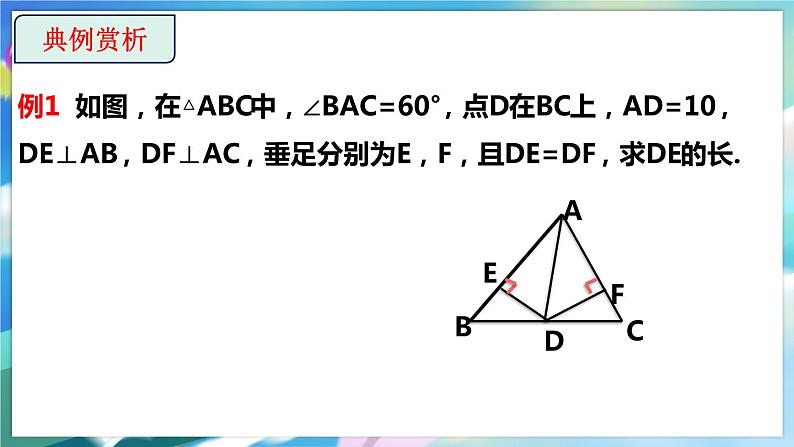
例1 如图，在△ABC中，∠BAC=60°，点D在BC上，AD=10，DE⊥AB，DF⊥AC，垂足分别为E，F，且DE=DF，求DE的长.
∵DE丄AB, DF丄AC，垂足分分别为E，F,且DE＝DF，∴AD平分∠BAC (在一个角的内部，到角的两边距离相等的点在这个角的平分线上）.又∵∠BAC＝60°，∴∠BAD＝30°. 在 Rt△ADE中，∠AED＝90°，AD＝10，∴DE＝ AD＝ ×10＝5 (在直角三角形中，如果一个锐角等于30°. 那么它所对的直角边等于斜边的一半).
你能写出这个定理的逆命题吗？它是真命题吗？
角的平分线上的点到角的两边的距离相等.
如果有一个点到角两边的距离相等，那么这个点必在这个角的平分线上．简写
这个命题是假命题．角平分线是角内部的一条射线，而角的外部也存在到角两边距离相等的点．
到角的两边距离相等的点，在这个角的平分线上
定理 在一个角的内部，到角的两边距离相等的点在这个角的平分线上.
书写格式：如图，∵PD⊥OA，PE⊥OB，PD＝PE, ∴点P在∠AOB的平分线上(或∠AOC＝∠BOC)
已知：如图，点 P 为∠AOB 内一点，且 PD⊥OA，PE⊥OB，D、E 为垂足且 PD = PE. 求证：OP平分∠AOB.
证明：∵PD丄OA, PE丄OB,垂足分别为D，E， ∴∠ODP＝∠OEP＝90°，∵PD＝PE，OP＝OP，∴Rt△DOP≌ Rt△EOP ( HL ).∴∠1＝∠2 (全等三角形的对应角相等).∴OP平分∠AOB.
例2 如图，已知BE＝CF，DF⊥AC于点F，DE⊥AB于点E，BF和CE相交于点D.求证：AD平分∠BAC.
证明：∵DF⊥AC于点F，DE⊥AB于点E， ∴∠DEB＝∠DFC＝90°. 在△BDE和△CDF中， ∴△BDE≌△CDF(AAS)． ∴DE＝DF.又∵DF⊥AC于点F，DE⊥AB于点E， ∴AD平分∠BAC.
1 如图，OP是∠AOB的平分线，点C，D分别在角的两边OA，OB上，添加下列条件，不能判定△POC≌△POD的选项是(　　)A．PC⊥OA，PD⊥OB B．OC＝ODC．∠OPC＝∠OPD D．PC＝PD
2 如图，在CD上求一点P，使它到边OA，OB的距离相等，则点P是(　　)A．线段CD的中点B．CD与过点O作CD的垂线的交点C．CD与∠AOB的平分线的交点D．以上均不对
3 如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE⊥AB于E，若AB＝6 cm，则△DBE的周长是(　　)A．6 B．7 cm C．8 cm D．9 cm
4 如图，在△ABC中，与∠ABC，∠ACB相邻的外角的平分线相交于点F，连接AF，则下列结论正确的是(　　)A．AF平分BC B．AF平分∠BACC．AF⊥BC D．以上结论都正确
5 如图，△ABC 中，AD 是∠BAC 的平分线， BD = CD， DE⊥AB，DF⊥AC，垂足分别为 E，F. 求证：EB = FC.