北师大版八年级下册4 角平分线练习题

这是一份北师大版八年级下册4 角平分线练习题，共9页。

一．选择题（共5小题，每题8分）
1．如图，某石油公司计划在三条公路围成的一块平地上建一个加油站，综合各种因素，要求这个加油站到三条公路的距离相等，则应建在（ ）
A．△ABC的三条内角平分线的交点处 B．△ABC的三条高线的交点处
C．△ABC三边的中垂线的交点处 D．△ABC的三条中线的交点处

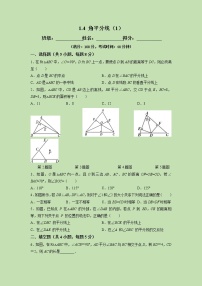
第1题图 第2题图 第3题图 第4题图 第5题图
2．△ABC中，点O是△ABC内一点，且点O到△ABC三边的距离相等，∠A=40°，则∠BOC的大小为（ ）
A．110° B．120° C．130° D．140°
3．如图，△ABC的三边AB、AC、BC的长分别为4、6、8，其三条角平分线将△ABC分成三个三角形，则S△OAB：S△OAC：S△OBC＝（ ）
A．2：3：4 B．1：1：1 C．1：2：3 D．4：3：2
4．如图，点P是Rt△ABC各内角平分线的交点，如果AB=3，BC=4，AC=5，PE⊥BC，那么PE=（ ）
A．1 B．1.5 C．2 D．2.4
5．如图，在△ABC中，∠ABC，∠ACB的平分线相交于点O，连接 AO并延长，交BC于点D，OH⊥BC于点H；若∠BAC=60°，OH=3cm，则OA=（ ）
A．6cm B．5cm C．4cm D．3cm
二．填空题（共4小题，每题5分）
6．如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直，垂足为A，交CD于D，若AD＝8，则点P到BC的距离是_____．

第1题图 第2题图 第3题图 第4题图
7．如图，△ABC的三条角平分线交于O点，已知△ABC的周长为20，OD⊥AB，OD=5，则△ABC的面积=_________.
8．如图，在△ABC中，∠A＝70°，∠ABC，∠ACB的平分线相交于点I，则∠BIC＝_______________．
9．如图,已知BE平分∠ABC,CE平分∠ACD,且交BE于点E,∠BAC=30°,则∠CAE=________.
三．解答题（共3小题，第10题10分，第11、12题各15分）
10．如图，直线l1，l2，l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有几处？请在图中标出来；
11．如图，在△ABC中，∠BAC的平分线BD与∠ACB的邻补角的平分线CE相交于点P； 求证：点P到△ABC三边所在直线的距离相等；
12．如图，△ABC的角平分线AD、BE相交于点P；
（1）在图①中，分别画出点P到△ABC的三边AC、BC、BA的垂线段PF、PG、PH，写出三条垂线段的数量关系，并说明理由；
（2）在图②中，∠ABC是直角，∠C=60º，其余条件不变，判断PE，PD之间的数量关系，并说明理由；

试题解析
1．A
【解析】三条公路围成一个三角形，三角形中到三边的距离相等的点是三角形的内心，即三条内角平分线的交点．
解：三角形中到三边的距离相等的是三角形的内心，即为三条内角平分线的交点.
故选A.
2．A
3．A
【解析】由角平分线的性质可得，点O到三角形三边的距离相等，即三个三角形的AB、BC、CA边上的高相等，利用面积公式即可求解．
解：过点O作OD⊥AB于D，OE⊥AC于E，OF⊥BC于F，
∵O是三角形三条角平分线的交点，
∴OD＝OE＝OF，
∵AB＝4，AC＝6，BC＝8，
∴S△OAB：S△OAC：S△OBC＝2：3：4．
故选：A．
4．A
【解析】根据角平分线的性质定理可得点P到各边的距离都相等，设点P到各边的距离为r，根据直角三角形面积的两种表示法可得12AC•BC=12（AC+BC+AB）•r，由此即可求得r的值，即为PE的值.
解：∵点P为三条角平分线的交点，
∴点P到各边的距离都相等，设点P到各边的距离为r，
∵Rt△ABC中，∠C是直角，O是角平分线的交点，AC=3，BC=4，AB=5，
∴S△ABC=12AC•BC=12（AC+BC+AB）•r，
∴3×4=（3+4+5）×r，
解得：r=1．
即PE=1.
故选A．
5．A
【解析】作OE⊥AB交AB于E，由OB平分∠ABC，OH⊥BC，根据角平分线的性质定理可得OE=OH=3cm，再由角平分线的定义得到∠BAO=30°，根据30°角直角三角形的性质即可求得OA的长．
解：作OE⊥AB交AB于E，
∵OB平分∠ABC，OH⊥BC，
∴OE=OH=3cm，
∵∠ABC，∠ACB的角平分线交于点O，
∴AO平分∠BAC，
∵∠BAC=60°，
∴∠BAO=30°，
∴AO=2OE=6cm，
故选A．
6．4
【解析】过点P作PE⊥BC于E，根据角平分线上的点到角的两边的距离相等，可得PA=PE，PD=PE，那么PE=PA=PD，又AD=8，进而求出PE=4．
解：如图，过点P作PE⊥BC于E，
∵AB∥CD，PA⊥AB，
∴PD⊥CD，
∵BP和CP分别平分∠ABC和∠DCB，
∴PA=PE，PD=PE，
∴PE=PA=PD，
∵PA+PD=AD=8，
∴PA=PD=4，
∴PE=4.
故答案为：4.
7．50.
【解析】根据△ABC的三条角平分线交于O点，故点O到三角形各边的距离相等，即△ABO、△ACO、△BCO的高相等，再把这三个三角形的面积加起来即为△ABC的面积.
解：∵△ABC的三条角平分线交于O点，
∴点O到三角形各边的距离相等，
即△ABO、△ACO、△BCO的高相等，h=5,
∵△ABC的周长为20，即AB+AC+BC=20,
∴S△ABC=S△ABO+S△ACO+S△BCO
=12AB×h+12AC×h+12BC×h
=12×（AB+AC+BC）×h
=12×20×5=50.
8．125°
【解析】根据三角形内角和定理求出∠ABC+∠ACB=180°-∠A=130°，根据角平分线定义得出∠IBC=12∠ABC，∠ICB=12∠ACB，求出∠IBC+∠ICB=65°，代入∠BIC=180°-（∠IBC+∠ICB）求出即可．
解：∵∠A=70°，
∴∠ABC+∠ACB=180°-∠A=110°，
∵∠ABC和∠ACB的角平分线交于I，
∴∠IBC=12∠ABC，∠ICB=12∠ACB，
∴∠IBC+∠ICB=12×110°=55°，
∴∠BIC=180°-（∠IBC+∠ICB）=125°，
故答案为：125°．
9．75°
【解析】如图过点E分别作EG⊥BD、EH⊥BA、EI⊥AC，垂足分别为G、H、I，根据角平分线的性质可得EH=EG，EI=EG，再根据角平分线的性质的逆定理可证AE平分∠FAC，再根据∠FAC与∠BAC互补即可．
解：如图所示：过点E分别作EG⊥BD、EH⊥BA、EI⊥AC，垂足分别为G、H、I，
∵BE平分∠ABC，EG⊥BD，EH⊥BA，
∴EH=EG．
∵CE平分∠ACD，EG⊥BD，EI⊥AC，
∴EI=EG，
∴EI=EH，
∵EH⊥BA，EI⊥AC，
∴AE平分∠FAC
∵∠BAC=30°
∴∠FAC=180°-∠BAC=150°
∴∠CAE=12∠FAC=75°
故答案为：75°
10．可供选择的地址有4处，图见解析
【解析】到三条相互交叉的公路距离相等的地点应是三条角平分线的交点．把三条公路的中心部位看作三角形，那么这个三角形两个内角平分线的交点以及三个外角两两平分线的交点都满足要求．由此即可求解.
解：满足条件的有：（1）三角形两个内角平分线的交点，共一处；（2）三个外角两两平分线的交点，共三处．
∴可供选择的地址有4处（如图所示）.
11．证明见解析.
【解析】过点P作三边AB、BC、CA所在直线的垂线,垂足分别是Q、M、N.根据角平分线性质定理即可证明结论.
证明：如图,过点P作三边AB、BC、CA所在直线的垂线,垂足分别是Q、M、N.则垂线段PQ、PM、PN,即为P点到三边AB、BC、CA所在直线的距离.
∵P是∠ABC的平分线BD上的一点,
∴PQ=PM.
∵P是∠ACM的平分线CE上的一点,
∴PN=PM.
∴PQ=PM=PN.
即点到三边AB、BC、CA所在直线的距离相等.
12．（1）PF=PG=PH；理由见解析；（2）PE=PD；理由见解析
【解析】（1）PF=PG=PH，根据已知条件及角平分线的性质定理即可证得结论；（2）过点P作PF⊥AC，PG⊥BC，垂足分别为F、G，证明△PFE≌△PGD，根据全等三角形的性质即可证得PE=PD．
证明：（1）如图1所示：
PF=PH=PG，理由如下：
∵AD平分∠BAC，PF⊥AC，PH⊥AB，
∴PF=PH，
∵BE平分∠ABC，PG⊥BC，PH⊥AB，
∴PG=PH，
∴PF=PH=PG；
（2）PE=PD．
证明：∵∠ABC=90°，∠C=60°，
∴∠CAB=30°，
∵AD平分∠BAC，BE平分∠ABC，
∴∠CAD=∠BAD=12∠CAB=15°，∠ABE=∠CBE=12∠ABC=45°，
过点P作PF⊥AC，PG⊥BC，垂足分别为F、G，
则∠PFE=∠PGD=90°，
∵∠PDG为△ADC的一个外角，
∴∠PDG=∠C+∠CAD=60°+12∠CAB=60°+15°=75°，
∵∠PEF是△ABE的一个外角，
∴∠PEF=∠CAB+∠ABE=30°+12∠CBA=30°+45°=75°，
∴∠PEF=∠PDG，
∵PF⊥AC，PG⊥BC，
∴∠PFE=∠PGD=90°，
由（1）得：PF=PG，
∴△PFE≌△PGD，
∴PE=PD．