初中数学北师大版八年级下册2 图形的旋转教课ppt课件

这是一份初中数学北师大版八年级下册2 图形的旋转教课ppt课件，共25页。PPT课件主要包含了新知导入，请同学们欣赏图片，新知讲解，做一做，图3-11，图3-12，想一想，图3-13，课堂练习，中考链接等内容，欢迎下载使用。

上面图片反映的是日常生活中物体运动的一些场景．你还能举出一些类似的例子吗？与同伴交流
在平面内，将一个图形绕一个定点按某个方向转动一个角度，这样的图形运动称为旋转（rtatin），这个定点称为旋转中心，转动的角称为旋转角. 旋转不改变图形的形状和大小
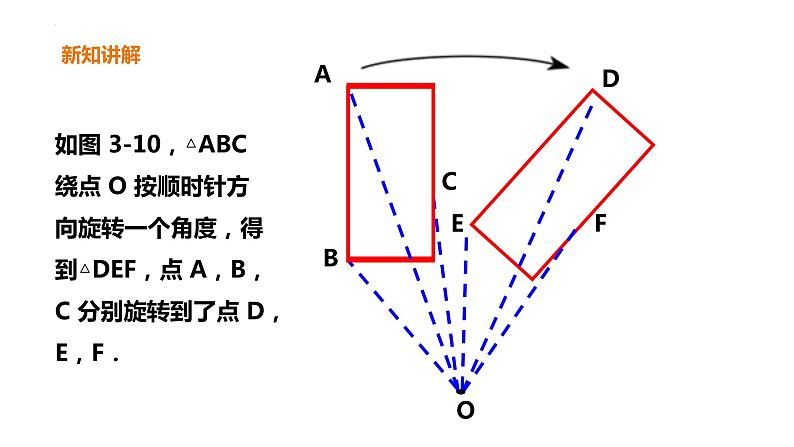
如图 3-10，△ABC 绕点 O 按顺时针方向旋转一个角度，得到△DEF，点 A，B，C 分别旋转到了点 D，E，F．
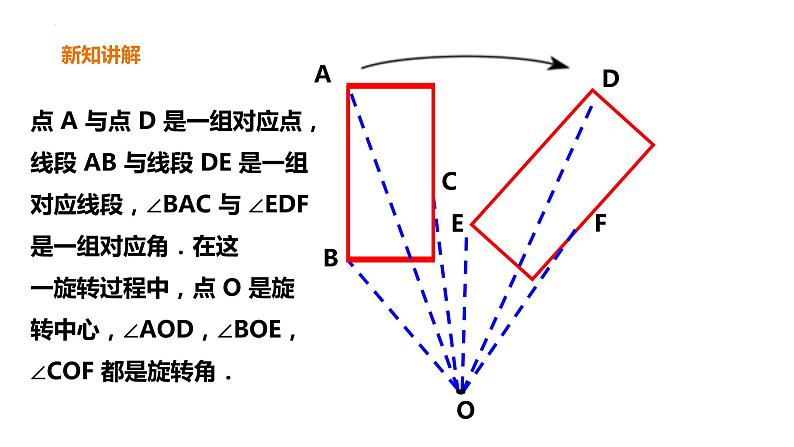
点 A 与点 D 是一组对应点，线段 AB 与线段 DE 是一组对应线段，∠BAC 与 ∠EDF 是一组对应角．在这一旋转过程中，点 O 是旋转中心，∠AOD，∠BOE，∠COF 都是旋转角．
如图 3-11，两张透明纸上的四边形 ABCD 和四边形 EFGH 完全重合，在纸上选取旋转中心 O，并将其固定．把其中一张纸片绕点 O 旋转一定角度（如图 3-12）．
（1）观察图 3-12 的两个四边形，你能发现有哪些相等的线段和相等的角？
相等的线段：AB=EF、BC=FG、 CD=GH、DA=HE相等的角：∠A= ∠ E、 ∠B= ∠ F、 ∠C= ∠ G、 ∠D= ∠ H
（2）连接 AO，BO，CO，DO，EO，FO，GO，HO，你又能发现有哪些相等的线段和相等的角？
相等的线段：AO= EO、 BO= FO、 CO= GO、 DO= HO相等的角：∠AOE= ∠ BOF=∠COG= ∠ DOH
（3）在图 3-12 中再取一些对应点，画出它们与旋转中心所连成的线段，你又能发现什么？
改变透明纸上所画图形的形状，再试一试，并与同伴交流．
一个图形和它经过旋转所得的图形中，对应点到旋转中心的距离相等，任意一组对应点与旋转中心的连线所成的角都等于旋转角；对应线段相等，对应角相等．
在图 3-13（1）~（4）的四个三角形中，哪个不能由△ABC 经过平移或旋转得到？
A为△ABC平移所得，CD为△ABC旋转所得。而B为图像△ABC轴对称图形
1、如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A'B'C，连接AA'，若∠1=25°，则∠BAA'的度数是( ) A. 55° B. 60° C. 65° D. 70°
解：∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A'B'C，∴AC=A'C，∴△ACA'是等腰直角三角形，∴∠CA'A=45°，∠CA'B'=20°=∠BAC ∴∠BAA'=180°-70°-45°=65°，故选：C．
2、如图，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB延长线上，连接AD.下列结论一定正确的是( )A. ∠ABD=∠EB. ∠CBE=∠CC. AD//BC D. AD=BC
解：∵△ABC绕点B顺时针旋转60°得△DBE，∴∠ABD=∠CBE=60°，AB=BD，∴△ABD是等边三角形，∴∠DAB=60°，∴∠DAB=∠CBE，∴AD//BC，故选：C．
如图所示，点P是等边三角形ABC内的一点，且PA=6，PB=8，PC=10，若将△PAC绕点A逆时针旋转后，得到△P'AB，则∠APB等于( ) A. 150° B. 105° C. 120° D. 90°
解：连结PP'，如图，∵△ABC为等边三角形，∴AB=AC，∠BAC=60°，∵△PAC绕点A逆时针旋转后，得到△P'AB，∴∠P'AP=60°，P'B=CP=10，AP'=AP=6，∴△APP'为等边三角形，∴∠APP'=60°，PP'=AP=6，
在△BPP'中，∵BP=8，PP'=6，P'B=10，∴PP'2+PB2=P'B2，∴△PBP'为直角三角形，∠P'PB=90°，∴∠APB=∠APP'+∠P'PB=60°+90°=150°．故选：A．
对应线段相等，对应角相等
对应点到旋转中心的距离相等
任意一对对应点与旋转中心的连线所成的角都等于旋转角；
图形上的每一点都绕旋转中心沿相同方向转动了相同的角度.