
河北省保定市莲池区贺阳外国语学校2021-2022学年七年级上学期期末考试数学试题(含答案)
展开2021-2022学年河北省保定市莲池区贺阳外国语学校七年级(上)期末数学试卷
一、选择题。(本大题有16个小题,共42分。1~10小题各3分;11~16小题各2分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(3分)一个几何体的侧面展开图如图所示,则该几何体的底面是( )
A. B.
C. D.
2.(3分)马拉松(Marathon)是国际上非常普及的长跑比赛项目,全程距离26英里385码,折合约为42000米,用科学记数法表示42000为( )
A.42×103 B.4.2×104 C.4.2×105 D.42000×105
3.(3分)已知a=b,下列等式不一定成立的是( )
A.a+c=b+c B.c﹣a=c﹣b C.ac=bc D.
4.(3分)为了解甲、乙、丙、丁四所学校学生对“122交通安全专题”相关知识的掌握情况,小明计划进行抽样调查,你认为以下方案中最合理的是( )
A.抽取甲校七年级学生进行调查
B.在四个学校随机抽取200名老师进行调查
C.在乙校中随机抽取200名学生进行调查
D.在四个学校各随机抽取200名学生进行调查
5.(3分)将方程=1去分母得到2(2x﹣1)﹣3x+1=6,错在( )
A.分母的最小公倍数找错
B.去分母时漏乘项
C.去分母时分子部分没有加括号
D.去分母时各项所乘的数不同
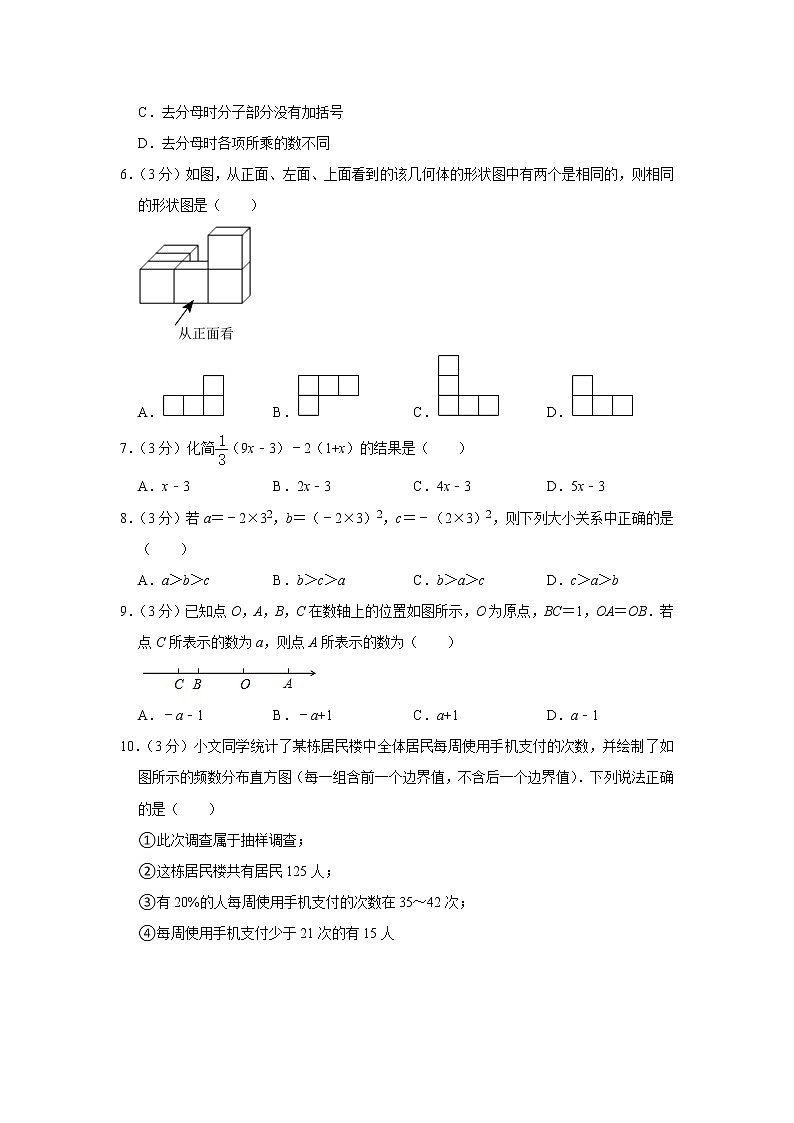
6.(3分)如图,从正面、左面、上面看到的该几何体的形状图中有两个是相同的,则相同的形状图是( )
A. B. C. D.
7.(3分)化简(9x﹣3)﹣2(1+x)的结果是( )
A.x﹣3 B.2x﹣3 C.4x﹣3 D.5x﹣3
8.(3分)若a=﹣2×32,b=(﹣2×3)2,c=﹣(2×3)2,则下列大小关系中正确的是( )
A.a>b>c B.b>c>a C.b>a>c D.c>a>b
9.(3分)已知点O,A,B,C在数轴上的位置如图所示,O为原点,BC=1,OA=OB.若点C所表示的数为a,则点A所表示的数为( )
A.﹣a﹣1 B.﹣a+1 C.a+1 D.a﹣1
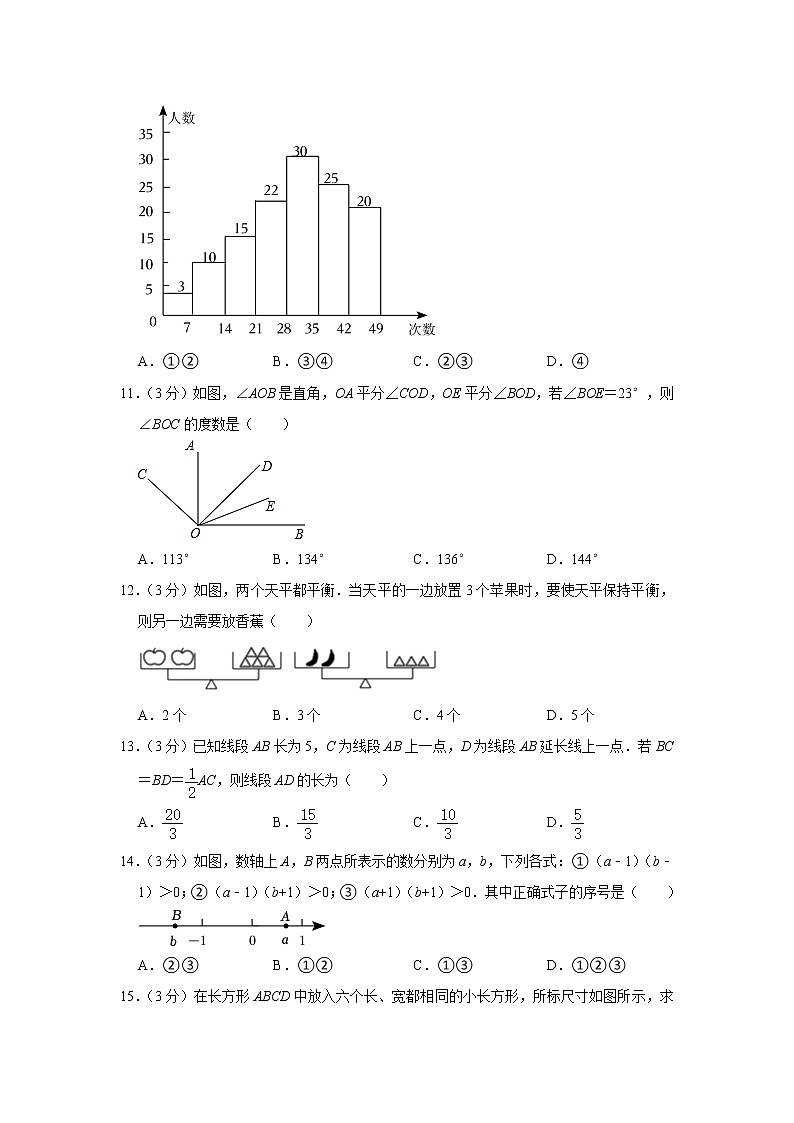
10.(3分)小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了如图所示的频数分布直方图(每一组含前一个边界值,不含后一个边界值).下列说法正确的是( )
①此次调查属于抽样调查;
②这栋居民楼共有居民125人;
③有20%的人每周使用手机支付的次数在35~42次;
④每周使用手机支付少于21次的有15人
A.①② B.③④ C.②③ D.④
11.(3分)如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
A.113° B.134° C.136° D.144°
12.(3分)如图,两个天平都平衡.当天平的一边放置3个苹果时,要使天平保持平衡,则另一边需要放香蕉( )
A.2个 B.3个 C.4个 D.5个
13.(3分)已知线段AB长为5,C为线段AB上一点,D为线段AB延长线上一点.若BC=BD=AC,则线段AD的长为( )
A. B. C. D.
14.(3分)如图,数轴上A,B两点所表示的数分别为a,b,下列各式:①(a﹣1)(b﹣1)>0;②(a﹣1)(b+1)>0;③(a+1)(b+1)>0.其中正确式子的序号是( )
A.②③ B.①② C.①③ D.①②③
15.(3分)在长方形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若设AE=x(cm),则由题意,得方程( )
A.14﹣3x=6 B.14﹣3x=6+2x
C.6+2x=x+(14﹣3x) D.6+2x=14﹣x
16.(3分)如图,若该模型第n层有4041个小三角形,则n的值为( )
A.2019 B.2020 C.2021 D.2022
二、填空题。(本大题有3个小题,每小题有2个空,每空2分,共12分把答案写在题中横线上)
17.(4分)若(a﹣2)xa+3+2=0是关于x的一元一次方程,则a= ,方程的解是 .
18.(4分)如图,点A,O,C在一条直线上,∠AOD=120°,且∠AOB:∠COD=3:5,则∠COD的度数为 ,∠BOC的度数为 .
19.(4分)对于有理数a,b,定义一种新运算“⊙”,规定:a⊙b=|a+b|+|a﹣b|.
(1)计算:2⊙(﹣4)= ;
(2)若a,b在数轴上的位置如图所示.则化简a⊙b= .
三、解答题。(本大题共7个小题,共66分。解答应写出文字说明、证明过程或演算步骤)
20.(8分)按要求解答下列各小题.
(1)计算:(﹣1)2+|2﹣5|÷(﹣3)×;
(2)解方程:2(x﹣3)﹣5(x+4)=4.
21.(9分)已知A=2x2﹣6ax+3,B=﹣7x2﹣8x﹣1,按要求完成下列各小题.
(1)若A+B的结果中不含x的一次项,则a的值为 ;
(2)当a=﹣2时,化简A﹣3B,再把x=﹣1代入求值.
22.(9分)如图,已知∠AOB=90°,∠BOC在∠AOB的外部,且OF平分∠BOC,OE平分∠AOC.
(1)当∠BOC=60°时,∠AOE的度数为 ,∠EOF的度数为 ;
(2)当∠BOC=α(0°<α<90°)时,求∠EOF的度数.
23.(9分)某校七年级1至4班计划每班购买数量相同的图书布置班级读书角,但是由于种种原因,实际购书量与计划有出入,下表是实际购书情况:
班级
1班
2班
3班
4班
实际购买量(本)
a
33
c
21
实际购买量与计划购数量的差值(本)
+12
b
﹣8
﹣9
(1)直接写出a= ,b= ,c=
(2)根据记录的数据可知4个班实际购书共 本
(3)书店给出一种优惠方案:一次购买不少于15本,其中2本书免费.若每本书售价为30元,请计算这4个班整体购书的最低总花费是多少元?
24.(9分)设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取某中学部分学生的体质健康综合评定成绩,整理绘制成如图所示的两幅不完整的统计图.请根据图中信息,解答下列问题.
(1)在这次调查中,一共抽取了 名学生,a= ;
(2)补全条形统计图;
(3)求扇形统计图中C级对应的扇形圆心角的度数.
25.(10分)进入四月份,樱桃开始上市,某水果商从批发市场用12000元购进了大樱桃和小樱桃各300千克,大樱桃的进价比小樱桃的进价每千克多20元,大樱桃售价为每千克40元,小樱桃售价为每千克15元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少钱?
(2)该水果商第二次仍用12000元从批发市场购进了大樱桃和小樱桃各300千克,进价不变,但在运输过程中大樱桃损耗了15%.若大樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的80%,小樱桃的售价最少应为多少?
26.(12分)已知数轴上有A、B两点,点A表示的数为﹣8,且AB=20.
(1)点B表示的数为 ;
(2)如图1,若点B在点A的右侧,点P以每秒4个单位的速度从点A出发向右匀速运动.
①若点Q同时以每秒2个单位的速度从点B出发向左匀速运动,经过多少秒后,点P与点Q相距1个单位?
②若点Q同时以每秒2个单位的速度从点B出发向右匀速运动,经过多少秒后,在点P、B、Q三点中,其中有一点是另外两个点连接所成线段的中点?
2021-2022学年河北省保定市莲池区贺阳外国语学校七年级(上)期末数学试卷
参考答案与试题解析
一、选择题。(本大题有16个小题,共42分。1~10小题各3分;11~16小题各2分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(3分)一个几何体的侧面展开图如图所示,则该几何体的底面是( )
A. B.
C. D.
【分析】根据几何体的侧面展开图可知该几何体为四棱锥,所以它的底面是四边形.
【解答】解:由题意可知,该几何体为四棱锥,所以它的底面是四边形.
故选:B.
【点评】本题主要考查了几何体的展开图,熟练掌握棱锥的展开图是解答本题的关键.
2.(3分)马拉松(Marathon)是国际上非常普及的长跑比赛项目,全程距离26英里385码,折合约为42000米,用科学记数法表示42000为( )
A.42×103 B.4.2×104 C.4.2×105 D.42000×105
【分析】根据把一个大于10的数记成a×10n的形式的方法进行求解,即可得出答案.
【解答】解:42000=4.2×104.
故选:B.
【点评】本题主要考查了科学记数法,熟练掌握科学记数法表示的方法进行求解是解决本题的关键.
3.(3分)已知a=b,下列等式不一定成立的是( )
A.a+c=b+c B.c﹣a=c﹣b C.ac=bc D.
【分析】根据等式的基本性质逐一判断可得.
【解答】解:A、由a=b知a+c=b+c,此选项一定成立;
B、由a=b知c﹣a=c﹣b,此选项一定成立;
C、由a=b知ac=bc,此选项一定成立;
D、由a=b知当c=0时无意义,此选项不一定成立;
故选:D.
【点评】本题主要考查了等式的基本性质,等式性质:1、等式的两边同时加上或减去同一个数或字母,等式仍成立;2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.
4.(3分)为了解甲、乙、丙、丁四所学校学生对“122交通安全专题”相关知识的掌握情况,小明计划进行抽样调查,你认为以下方案中最合理的是( )
A.抽取甲校七年级学生进行调查
B.在四个学校随机抽取200名老师进行调查
C.在乙校中随机抽取200名学生进行调查
D.在四个学校各随机抽取200名学生进行调查
【分析】根据抽样调查的具体性和代表性解答即可.
【解答】解:为了解甲、乙、丙、丁四所学校学生对“122交通安全专题”相关知识的掌握情况,在四个学校各随机抽取200名学生进行调查最具有具体性和代表性;
故选:D.
【点评】此题考查抽样调查,关键是理解抽样调查的具体性和代表性.
5.(3分)将方程=1去分母得到2(2x﹣1)﹣3x+1=6,错在( )
A.分母的最小公倍数找错
B.去分母时漏乘项
C.去分母时分子部分没有加括号
D.去分母时各项所乘的数不同
【分析】根据等式的性质,将方程=1去分母得到2(2x﹣1)﹣3x+1=6,错在去分母时分子部分没有加括号,应该是:2(2x﹣1)﹣3(x+1)=6.
【解答】解:将方程=1去分母得到2(2x﹣1)﹣3x+1=6,错在去分母时分子部分没有加括号.
故选:C.
【点评】此题主要考查了解一元一次方程的方法,要熟练掌握,注意等式的性质的应用.
6.(3分)如图,从正面、左面、上面看到的该几何体的形状图中有两个是相同的,则相同的形状图是( )
A. B. C. D.
【分析】根据从正面看得到的图形是主视图,从左边看得到的图形是左视图,从上边看得到的图形是俯视图,可得答案.
【解答】解:主视图和左视图相同,均为两层,底层是三个小正方形,上层的右边是一个小正方形.
故选:A.
【点评】本题考查了从不同方向看几何体,解题的关键是发挥空间想象能力,根据几何体的构造得到不同方向的平面图形.
7.(3分)化简(9x﹣3)﹣2(1+x)的结果是( )
A.x﹣3 B.2x﹣3 C.4x﹣3 D.5x﹣3
【分析】先去括号,然后合并同类项即可.
【解答】解:(9x﹣3)﹣2(1+x)
=3x﹣1﹣2﹣2x
=x﹣3,
故选:A.
【点评】本题考查整式的加减,解答本题的关键是明确去括号法则和合并同类项的方法.
8.(3分)若a=﹣2×32,b=(﹣2×3)2,c=﹣(2×3)2,则下列大小关系中正确的是( )
A.a>b>c B.b>c>a C.b>a>c D.c>a>b
【分析】分别计算出各数,再根据有理数比较大小的法则进行比较即可.
【解答】解:∵a=﹣2×32=﹣2×9=﹣18,b=(﹣2×3)2=36,c=﹣(2×3)2=﹣36,
又∵36>﹣18>﹣36,
∴b>a>c.
故选:C.
【点评】本题考查的是有理数的乘方及有理数比较大小的法则,比较简单.
9.(3分)已知点O,A,B,C在数轴上的位置如图所示,O为原点,BC=1,OA=OB.若点C所表示的数为a,则点A所表示的数为( )
A.﹣a﹣1 B.﹣a+1 C.a+1 D.a﹣1
【分析】根据题意和数轴可以用含a的式子表示出点B表示的数,本题得以解决.
【解答】解:∵O为原点,BC=1,OA=OB,点C所表示的数为a,
∴点B表示的数为a+1,
∴点A表示的数为:﹣(a+1)=﹣a﹣1,
故选:A.
【点评】本题考查数轴,解答本题的关键是明确题意,利用数形结合的思想解答.
10.(3分)小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了如图所示的频数分布直方图(每一组含前一个边界值,不含后一个边界值).下列说法正确的是( )
①此次调查属于抽样调查;
②这栋居民楼共有居民125人;
③有20%的人每周使用手机支付的次数在35~42次;
④每周使用手机支付少于21次的有15人
A.①② B.③④ C.②③ D.④
【分析】根据直方图表示的意义求得统计的总人数,以及每组的人数即可判断.
【解答】解:①此次调查属于全面调查;此结论错误;
②这栋居民楼共有居民3+10+15+22+30+25+20=125人,此结论正确;
③每周使用手机支付的次数在35~42次所占百分比为×100%=20%,此结论正确;
④每周使用手机支付少于21次的有15人3+10+15=28人,此结论错误;
故选:C.
【点评】本题考查了全面调查与抽样调查,读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
11.(3分)如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
A.113° B.134° C.136° D.144°
【分析】首先根据OE平分∠BOD,∠BOE=23°,求出∠BOD的度数是多少;然后根据∠AOB是直角,求出∠AOD的度数,再根据OA平分∠COD,求出∠COD的度数,据此求出∠BOC的度数是多少即可.
【解答】解:∵OE平分∠BOD,∠BOE=23°,
∴∠BOD=23°×2=46°;
∵∠AOB是直角,
∴∠AOD=90°﹣46°=44°,
又∵OA平分∠COD,
∴∠COD=2∠AOD=2×44°=88°,
∴∠BOC=∠BOD+∠COD=46°+88°=134°.
故选:B.
【点评】此题主要考查了角的计算,以及角平分线的含义和求法,要熟练掌握.
12.(3分)如图,两个天平都平衡.当天平的一边放置3个苹果时,要使天平保持平衡,则另一边需要放香蕉( )
A.2个 B.3个 C.4个 D.5个
【分析】通过等量关系,建立方程求解.
【解答】解:设一个苹果的重量是a,一个香蕉的重量是b,一根三角形物体的重量是c,由题意得:
,
∴,
∴3a==,
=5(个),
即另一边需要放香蕉5个.
故选:D.
【点评】本题考查等式性质,找到题中的等量关系是求解本题的关键.
13.(3分)已知线段AB长为5,C为线段AB上一点,D为线段AB延长线上一点.若BC=BD=AC,则线段AD的长为( )
A. B. C. D.
【分析】利用线段的和差和等量关系用AC表示AB,根据AB=5即可得出AD.
【解答】解:根据题意可知,
∵BC=BD=AB,
∴AD=AB+BD=AB+AB=AB,
∵AB=5,
∴AD=AB
=×5
=.
故选:A.
【点评】本题考查了线段的和差,掌握题意正确找出线段之间的数量关系是关键.
14.(3分)如图,数轴上A,B两点所表示的数分别为a,b,下列各式:①(a﹣1)(b﹣1)>0;②(a﹣1)(b+1)>0;③(a+1)(b+1)>0.其中正确式子的序号是( )
A.②③ B.①② C.①③ D.①②③
【分析】因为数轴上右边的数总比左边的大,大数减小数差为正,小数减大数差为负.再根据乘法运算同号得正,异号得负.
【解答】解:∵a<1,
∴a﹣1<0.
∵b<1,
∴b﹣1<0.
∴(a﹣1)(b﹣1)>0.
∴①正确,故①符合题意.
∵b<﹣1,
∴b﹣(﹣1)<0.即b+1<0,
∴(a﹣1)(b+1)>0.
∴②正确,故②符合题意.
∵a>0,
∴a+1>0,
又∵b<﹣1,
∴b+1<0,
∴(a+1)(b+1)<0.
∴③错误.故③不合题意.
故选:B.
【点评】本题考查数轴上点的大小的比较,还考查了两个数相乘,积的符号问题.
15.(3分)在长方形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若设AE=x(cm),则由题意,得方程( )
A.14﹣3x=6 B.14﹣3x=6+2x
C.6+2x=x+(14﹣3x) D.6+2x=14﹣x
【分析】设AE=xcm,观察图形结合小长方形的长不变,即可得出关于x的一元一次方程,此题得解.
【解答】解:设AE为xcm,
由题意得:6+2x=x+(14﹣3x)
故选:C.
【点评】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.
16.(3分)如图,若该模型第n层有4041个小三角形,则n的值为( )
A.2019 B.2020 C.2021 D.2022
【分析】第1层有1个小三角形,第2层有3个小三角形,第3层有5个小三角形,第4层有7个小三角形,第5层有9个小三角形,…,从而可求得第n层小三角形的个数,从而可求解.
【解答】解:∵第1层有1个小三角形,
第2层有3个小三角形,
第3层有5个小三角形,
第4层有7个小三角形,
第5层有9个小三角形,
…,
∴第n层中小三角形的个数为:2n﹣1,
∵第n层有4041个小三角形,
∴2n﹣1=4041,
解得:n=2021.
故选:C.
【点评】本题主要考查图形的变化规律,解答的关键是由所给的图形总结出存在的规律.
二、填空题。(本大题有3个小题,每小题有2个空,每空2分,共12分把答案写在题中横线上)
17.(4分)若(a﹣2)xa+3+2=0是关于x的一元一次方程,则a= ﹣2 ,方程的解是 x= .
【分析】利用一元一次方程的定义判断求出a的值,即可确定出方程的解.
【解答】解:∵(a﹣2)xa+3+2=0是关于x的一元一次方程,
∴a+3=1,且a﹣2≠0,
解得:a=﹣2,
方程为﹣4x+2=0,
解得:x=,
故答案为:﹣2;x=.
【点评】此题考查了一元一次方程的定义,熟练掌握一元一次方程的定义是解本题的关键.
18.(4分)如图,点A,O,C在一条直线上,∠AOD=120°,且∠AOB:∠COD=3:5,则∠COD的度数为 60° ,∠BOC的度数为 144° .
【分析】根据平角的定义以及图形中各个角之间的关系进行计算即可.
【解答】解:∵点A,O,C在一条直线上,∠AOD=120°,
∴∠COD=180°﹣120°=60°,
∵∠AOB:∠COD=3:5,
∴∠AOB=60°×=36°,
∴∠BOC=180°﹣36°=144°,
故答案为:60°;144°.
【点评】本题考查角的计算,掌握平角的定义以及图形中各个角之间的和差关系是正确解答的前提.
19.(4分)对于有理数a,b,定义一种新运算“⊙”,规定:a⊙b=|a+b|+|a﹣b|.
(1)计算:2⊙(﹣4)= 8 ;
(2)若a,b在数轴上的位置如图所示.则化简a⊙b= ﹣2a .
【分析】(1)根据新定义的运算,把相应的值代入运算即可;
(2)由数轴可得:a<0<b,且|a|>|b|,从而有a+b<0,a﹣b<0,再进行化简即可.
【解答】解:(1)2⊙(﹣4)
=|2+(﹣4)|+|2﹣(﹣4)|
=|﹣2|+|2+4|
=2+6
=8,
故答案为:8;
(2)由数轴得:a<0<b,且|a|>|b|,
∴a+b<0,a﹣b<0,
∴a⊙b
=|a+b|+|a﹣b|
=﹣(a+b)+[﹣(a﹣b)]
=﹣a﹣b﹣a+b
=﹣2a,
故答案为:﹣2a.
【点评】本题主要考查有理数的混合运算,数轴,解答的关键是对相应的运算法则的掌握.
三、解答题。(本大题共7个小题,共66分。解答应写出文字说明、证明过程或演算步骤)
20.(8分)按要求解答下列各小题.
(1)计算:(﹣1)2+|2﹣5|÷(﹣3)×;
(2)解方程:2(x﹣3)﹣5(x+4)=4.
【分析】(1)原式先算乘方及绝对值运算,再算乘除运算,最后算减法运算即可求出值;
(2)方程去括号,移项,合并同类项,把x系数化为1,即可求出解.
【解答】解:(1)原式=1+|﹣3|÷(﹣3)×
=1+3÷(﹣3)×
=1﹣
=;
(2)去括号得:2x﹣6﹣5x﹣20=4,
移项得:2x﹣5x=4+6+20,
合并同类项得:﹣3x=30,
解得:x=﹣10.
【点评】此题考查了解一元一次方程,以及有理数的混合运算,熟练掌握一元一次方程的解法及运算法则是解本题的关键.
21.(9分)已知A=2x2﹣6ax+3,B=﹣7x2﹣8x﹣1,按要求完成下列各小题.
(1)若A+B的结果中不含x的一次项,则a的值为 ﹣ ;
(2)当a=﹣2时,化简A﹣3B,再把x=﹣1代入求值.
【分析】(1)将已知等式代入,结合合并同类项的运算法则进行化简,然后令含x的一次项的系数为零,从而列方程求解;
(2)将已知等式代入,然后去括号,合并同类项进行化简,最后代入求值.
【解答】解:(1)∵A=2x2﹣6ax+3,B=﹣7x2﹣8x﹣1,
∴A+B=(2x2﹣6ax+3)+(﹣7x2﹣8x﹣1)
=2x2﹣6ax+3﹣7x2﹣8x﹣1
=﹣5x2﹣(6a+8)+2,
∵A+B的结果中不含x的一次项,
∴6a+8=0,
解得:a=﹣,
故答案为:﹣;
(2)∵A=2x2﹣6ax+3,B=﹣7x2﹣8x﹣1,且a=﹣2,
∴A=2x2﹣6×(﹣2)x+3=2x2+12x+3,
∴A﹣3B=2x2+12x+3﹣3(﹣7x2﹣8x﹣1)
=2x2+12x+3+21x2+24x+3
=23x2+36x+6,
当x=﹣1时,
原式=23×(﹣1)2+36×(﹣1)+6
=23×1﹣36+6
=23﹣36+6
=﹣7.
【点评】本题考查整式的加减—化简求值,掌握合并同类项(系数相加,字母及其指数不变)和去括号的运算法则(括号前面是“+”号,去掉“+”号和括号,括号里的各项不变号;括号前面是“﹣”号,去掉“﹣”号和括号,括号里的各项都变号)是解题关键.
22.(9分)如图,已知∠AOB=90°,∠BOC在∠AOB的外部,且OF平分∠BOC,OE平分∠AOC.
(1)当∠BOC=60°时,∠AOE的度数为 75° ,∠EOF的度数为 45° ;
(2)当∠BOC=α(0°<α<90°)时,求∠EOF的度数.
【分析】(1)∠AOE=∠AOC,根据角平分线的性质计算出∠EOC的度数,计算出∠BOF的度数,然后根据角的和差关系即可算出∠EOF的度数;
(2)首先求出∠AOC的度数,再根据角平分线的性质计算出∠EOC的度数,计算出∠BOF的度数,然后根据角的和差关系即可算出∠EOF的度数.
【解答】解:(1)∵∠AOB=90°,∠BOC=60°,
∴∠AOC=∠AOB+∠BOC=150°,
∵OE平分∠AOC,
∴∠AOE=∠EOC=∠AOC=×150°=75°,
又∵OF平分∠BOC,
∴∠FOC=∠BOC=×60°=30°,
∴∠EOF=∠EOC﹣∠FOC=75°﹣30°=45°;
故答案为:75°,45°;
(2)∵OF 平分∠BOC,
∴∠BOF=∠FOC=∠BOC=α,
∵OE 平分∠AOC,
∴∠AOE=∠EOC=(∠AOB+∠BOC)=( 90°+α ),
∴∠EOF=∠EOC﹣∠FOC=( 90°+α )﹣α=45°.
【点评】此题主要考查了角的平分线定义及性质,解决此题的关键是计算出∠EOC和∠BOF的度数.
23.(9分)某校七年级1至4班计划每班购买数量相同的图书布置班级读书角,但是由于种种原因,实际购书量与计划有出入,下表是实际购书情况:
班级
1班
2班
3班
4班
实际购买量(本)
a
33
c
21
实际购买量与计划购数量的差值(本)
+12
b
﹣8
﹣9
(1)直接写出a= 42 ,b= 3 ,c= 22
(2)根据记录的数据可知4个班实际购书共 118 本
(3)书店给出一种优惠方案:一次购买不少于15本,其中2本书免费.若每本书售价为30元,请计算这4个班整体购书的最低总花费是多少元?
【分析】根据正负数表示相反意义的量,可用正负数表示各数,根据有理数的加法,可得答案.
【解答】解:(1)a=21+9+12=42,b=33﹣30=3,c=30﹣8=22,
故答案为:42,+3,22;
(2)4个班一共购买数量=42+33+22+21=118(本);
故答案为:118;
(3)如果每次购买15本,则可以购买7次,且最后还剩13本书单独购买,
即最低总花费=30×(15﹣2)×7+30×13=3120(元).
【点评】本题考查了正数和负数,利用正数和负数表示相反意义的量,利用了有理数的加法运算.
24.(9分)设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取某中学部分学生的体质健康综合评定成绩,整理绘制成如图所示的两幅不完整的统计图.请根据图中信息,解答下列问题.
(1)在这次调查中,一共抽取了 50 名学生,a= 24 ;
(2)补全条形统计图;
(3)求扇形统计图中C级对应的扇形圆心角的度数.
【分析】(1)根据B级的人数和所占的百分比求出抽取的总人数,再用A级的人数除以总数即可求出a;
(2)用抽取的总人数减去A、B、D的人数,求出C级的人数,从而补全统计图;
(3)用360度乘以C级所占的百分比即可求出扇形统计图中C级对应的圆心角的度数.
【解答】解:(1)在这次调查中,一共抽取的学生数是:=50(人),
a=×100%=24%;
故答案为:50,24;
(2)等级为C的人数是:50﹣12﹣24﹣4=10(人),
补图如下:
(3)扇形统计图中C级对应的圆心角为×360°=72°.
【点评】此题考查了是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
25.(10分)进入四月份,樱桃开始上市,某水果商从批发市场用12000元购进了大樱桃和小樱桃各300千克,大樱桃的进价比小樱桃的进价每千克多20元,大樱桃售价为每千克40元,小樱桃售价为每千克15元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少钱?
(2)该水果商第二次仍用12000元从批发市场购进了大樱桃和小樱桃各300千克,进价不变,但在运输过程中大樱桃损耗了15%.若大樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的80%,小樱桃的售价最少应为多少?
【分析】(1)设小樱桃的进价是每千克x元,则大樱桃的进价是每千克(x+20)元,利用总价=单价×数量,即可得出关于x的一元一次方程,解之即可得出小樱桃的进价,将其代入(x+20)中可求出大樱桃的进价,再利用总利润=每千克的利润×销售数量,即可求出销售完后水果商获得的利润;
(2)设小樱桃的售价为每千克m元,利用总利润=销售单价×销售数量﹣进货总价,结合总利润不少于第一次所赚钱的80%,即可得出关于m的一元一次不等式,解之取其中的最小值即可得出小樱桃的售价最少为每千克18元.
【解答】解:(1)设小樱桃的进价是每千克x元,则大樱桃的进价是每千克(x+20)元,
依题意得:300x+300(x+20)=12000,
解得:x=10,
∴x+20=10+20=30,
∴(40﹣30)×300+(15﹣10)×300=10×300+5×300=3000+1500=4500(元).
答:大樱桃的进价是每千克30元,小樱桃的进价是每千克10元,销售完后,该水果商共赚了4500元钱.
(2)设小樱桃的售价为每千克m元,
依题意得:300×(1﹣15%)×40+300m﹣12000≥4500×80%,
解得:m≥18.
答:小樱桃的售价最少为每千克18元.
【点评】本题考查了一元一次方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出一元一次方程;(2)根据各数量之间的关系,正确列出一元一次不等式.
26.(12分)已知数轴上有A、B两点,点A表示的数为﹣8,且AB=20.
(1)点B表示的数为 12或﹣28 ;
(2)如图1,若点B在点A的右侧,点P以每秒4个单位的速度从点A出发向右匀速运动.
①若点Q同时以每秒2个单位的速度从点B出发向左匀速运动,经过多少秒后,点P与点Q相距1个单位?
②若点Q同时以每秒2个单位的速度从点B出发向右匀速运动,经过多少秒后,在点P、B、Q三点中,其中有一点是另外两个点连接所成线段的中点?
【分析】(1)根据数轴上两点间的距离公式可得答案;
(2)分两种情况:①设经过t秒后,点P与点Q相距1个单位,当点P与点Q未相遇,当点P与点Q未相遇过后时列方程求解即可;②设经过t少后其中一点为中点,分当P为中点时,当B为中点时,当Q为中点时,三种情况列方程求解即可.
【解答】解:(1)∵点A表示的数为﹣8,
∴点A到原点O的距离AO=8,
∵AB=20,
∴BO=AB﹣AO=20﹣8=12,
当点B在原点O的右侧时,
点B表示的数为12,
当点B在原点O的左侧时,点B表示的数为﹣28,
故答案为:12或﹣28.
(2)①设经过t秒后,点P与点Q相距1个单位,
当点P与点Q未相遇,2t+4t=20﹣1,
6t=19,
t=;
当点P与点Q相遇过后时,2t+4t=20+1,
6t=21,
t=.
综上分析:t=或t=.
②设经过t少后其中一点为中点,P=4t﹣8,B=12,Q=2t+12,
当P为中点时,B+Q=2P,12+2t=2(4t﹣8),t=;
当B为中点时,P+Q=2B,4t﹣8+2t+12=2×12,t=;
当Q为中点时,P+B=2Q,4t﹣8+12=2(2t+12),方程无解,
综上分析:t=或t=.
【点评】此题考查的是一元一次方程的应用,掌握分类讨论法分别求解是解决此题关键.
河北省保定市莲池区2023-2024学年上学期七年级上学期期末数学试题: 这是一份河北省保定市莲池区2023-2024学年上学期七年级上学期期末数学试题,共8页。
河北省保定市莲池区河北保定师范附属学校2022-2023学年九年级上学期月考数学试题答案: 这是一份河北省保定市莲池区河北保定师范附属学校2022-2023学年九年级上学期月考数学试题答案,共24页。试卷主要包含了 下列方程中是一元二次方程的是, 一元二次方程的解是, 矩形具有而菱形不具有的性质是, 下列命题中正确的是等内容,欢迎下载使用。
河北省保定市莲池区河北保定师范附属学校2022-2023学年九年级上学期月考数学试题: 这是一份河北省保定市莲池区河北保定师范附属学校2022-2023学年九年级上学期月考数学试题,共7页。试卷主要包含了 下列方程中是一元二次方程的是, 一元二次方程的解是, 矩形具有而菱形不具有的性质是, 下列命题中正确的是等内容,欢迎下载使用。












