河北省保定市莲池区河北保定师范附属学校2022-2023学年九年级上学期11月月考数学试题(含答案)

九年级数学网课质量监测试卷

一. 选择题（共15小题）

1. 下列关系式中，是的反比例函数的是（   ）

A.     B.    C.    D.
【分析】根据反比例函数的定义判断即可.
【解答】解：A. ，是正比例函数，故A不符合题意；

B. 是二次函数，故B不符合题意；

C. ，是的反比例函数，故C符合题意；

D. ，不是的反比例函数，故D不符合题意；

故选：C.

【点评】本题考查了反比例函数的定义，熟练掌握反比例函数的定义是解题的关键.

2. 已知中，，则等于（   ）

A. 6     B.     C. 10     D. 8
【分析】根据锐角三角函数的定义即可求出答案.
【解答】解：∵

∴.

∴

∴，

故选：C.

【点评】本题考查锐角三角函数，解题的关键是熟练运用锐角三角函数的定义，本题属于基础题型.

3. 如图所示，下列几何体中主视图是圆的是（   ）

A.  B.  C.  D.

【分析】根据球体、圆锥、圆柱、正方体的主视图的形状进行判断即可.
【解答】解：球体的主视图是圆，圆锥体的主视图是三角形，圆柱的主视图是长方形，正方体的主视图是正方形，故选：A.

【点评】本题考查简单几何体的三视图，掌握圆柱、圆锥、正方体、球的三视图的形状是正确判断的前提.

4. 某人沿着坡度为的山坡前进了米，则此人所在的位置升高了（   ）

A. 100米    B. 50米    C. 50米    D. 米

【分析】设此人所在的位置升高了米，根据坡度的概念用表示出此人前进的水平距离，根据勾股定理计算，得到答案.
【解答】解：设此人所在的位置升高了米，

∵斜坡的坡度为

∴此人前进的水平距离为米，

由勾股定理得：，

解得：（负值舍去），

∴此人所在的位置升高了100米，

故选：A.

【点评】本题考查的是解直角三角形的应用-坡度坡角问题，熟记坡度是坡面的铅直高度和水平宽度的比是解题的关键.

5. 如图，某同学下晚自习后经过一路灯回寝室，他从处背着灯柱方向走到处，在这一过程中他在该路灯灯光下的影子（   ）

A. 由长逐渐变短  B. 由短逐渐变长

C. 先变长后变短  D. 先变短后变长
【分析】因为等高的物体垂直地面放置时，在灯光下，离点光源近的物体的影子短，离点光源远的物体的影子长；已知人是从点处背着灯柱方向走到处，也就是从光源近处走向光源远处，据此进行解答.

【解答】解：根据中心投影的特征可知人远离灯光时，其影子逐渐变长.

故选：B.

【点评】本题主要考查的是中心投影的相关知识，解题的关键是明确中心投影的特征.

6. 学校的操场上竖着一根旗杆，在天晴的日子里，从早到晚这段时间里，旗杆的影子长度（   ）

A. 保持不变 B. 逐渐变长

C. 逐渐变短 D. 先逐渐变短，后又逐渐变长
【分析】白天太阳从东边逐渐移到旗杆的顶部，对应的影子逐渐变短.
【解答】解：学校的操场上竖着一根旗杆，在天晴的日子里，从早到晚这段时间里，旗杆的影子长度先逐渐变短，

后又逐渐变长.

故选：D.

【点评】本题侧重考查有关中心投影的题目，掌握其特点是解决此题的关键.

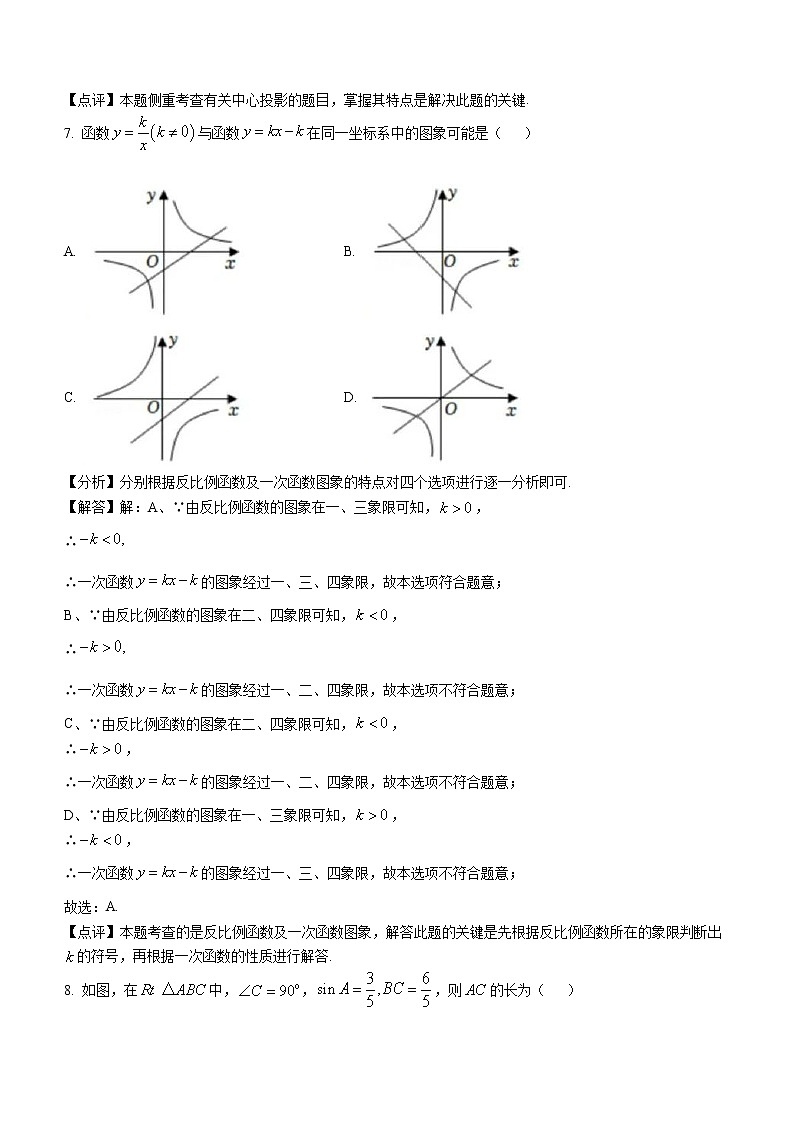
7. 函数与函数在同一坐标系中的图象可能是（   ）

A.  B.

C.  D.

【分析】分别根据反比例函数及一次函数图象的特点对四个选项进行逐一分析即可.
【解答】解：A、∵由反比例函数的图象在一、三象限可知，，

∴

∴一次函数的图象经过一、三、四象限，故本选项符合题意；

B、∵由反比例函数的图象在二、四象限可知，，

∴

∴一次函数的图象经过一、二、四象限，故本选项不符合题意；

C、∵由反比例函数的图象在二、四象限可知，，

∴，

∴一次函数的图象经过一、二、四象限，故本选项不符合题意；

D、∵由反比例函数的图象在一、三象限可知，，

∴，

∴一次函数的图象经过一、三、四象限，故本选项不符合题意；

故选：A.

【点评】本题考查的是反比例函数及一次函数图象，解答此题的关键是先根据反比例函数所在的象限判断出的符号，再根据一次函数的性质进行解答.

8. 如图，在中，，，则的长为（   ）

A.     B. 3     C.      D. 2
【分析】先利用正弦的定义求出，然后利用勾股定理计算出的长.
【解答】解：∵

∴，

∴.

故选：C.

【点评】本题考查了锐角三角函数的定义：在中，，把锐角的对边与斜边的比叫做的正弦，记作.

9. 苏州虎丘塔是我国江南著名的园林景点. 它建成于宋代（961年），共7层，高米. 由于地基的原因，塔身自400年前就开始向西北方向倾斜. 据测量，至今塔顶的中心偏离底层中心铅垂线的角度为，被称为“东方比萨斜塔”. 如今虎丘塔塔顶的中心偏离底层中心铅垂线的距离是（   ）米

A.    B.    C.    D.
【分析】根据正弦的定义计算，得到答案
【解答】解：在中，

则（米），

∴如今虎丘塔塔顶的中心偏离底层中心铅垂线的距离是米，

故选：B.

【点评】本题考查的是解直角三角形的应用-坡度坡角问题，掌握锐角三角函数的定义是解题的关键，

10. 若点都在反比例函数的图象上，则，，的大小关系是

（   ）

A.   B.   C.   D.
【分析】将点分别代入反比例函数，求得，，的值后，再来比较一下它们的大小.
【解答】解：∵点都在反比例函数的图象上，

∴

∴

故选：D.

【点评】本题考查了反比例函数图象上点的坐标特征，所有反比例函数图象上的点的坐标都满足该函数的解析式.

11. 若反比例函数的图象经过点，则该反比例函数的图象在（   ）

A. 第一、二象限  B. 第二、四象限

C. 第二、三象限  D. 第一、三象限
【分析】把已知点的坐标代入可求出值，然后根据反比例函数的性质即可判断.
【解答】解：∵反比例函数的图象经过点，

∴，

∴该反比例函数的图象在第一、三象限，

故选：D.

【点评】本题考查了待定系数法求反比例函数解析式，反比例函数图象上点的坐标特征，反比例函数的性质，求得的值是解题的关键.

12. 已知反比例函数，下列结论不正确的是（   ）

A. 图象经过点 B. 图象在第一、三象限

C. 随着的增大而减小 D. 当时，
【分析】把代入可判断A；根据反比例函数的性质可判断B，C，D.
【解答】解：A. 当时，，即该函数过点，故结论正确，选项A不符合题意；

B. ∵反比例函数

该函数图象为第一、三象限，故结论正确，选项B不符合题意；

C. ∵反比例函数

∴在每个象限内，随的增大而减小，故结论错误，选项C符合题意；

D. ∵反比例函数

∴该函数图象为第一、三象限，在每个象限内，随的增大而减小，

∵当时，，

∴当时，，故结论正确，选项D不符合题意；

故选：C.

【点评】本题主要考查了反比例函数的性质，能熟练地根据反比例函数的性质进行判断是解此题的关键.

13. 如图，在平面直角坐标系中，点是函数图象上的一点，且点在第一象限，过点作轴于点，作轴于点. 若四边形的面积为6，则的值为（   ）

A. 3  B. -3  C. 6  D. -6
【分析】因为过双曲线上任意一点引轴、轴垂线，所得矩形面积是个定值，即. 再由函数图象所在的象限确定的值即可.
【解答】解：∵点是反比例函数图象上的一点，分别过点作轴于点，轴于点B. 若四边形的面积为6，

∴矩形的面积，

解得.

又∵反比例函数的图象在第一象限，

∴.

故选：C.

【点评】本题主要考查了反比例函数中的几何意义，即过双曲线上任意一点引轴、轴垂线，所得矩形面积为，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解的几何意义.

14. 如图，的顶点在正方形网格的格点上，则的值为（   ）

A.     B. 1     C.     D.
【分析】根据网格构造直角三角形，利用网格以及勾股定理求出边长，再根据锐角三角函数的定义进行计算即可.
【解答】解：如图，延长交网格于点，连接，由网格以及正方形的性质可得，

由网格构造直角三角形可得，

在中，，

故选：A.

【点评】本题考查解直角三角形，构造直角三角形是解决问题的前提，利用网格和勾股定理求出边长是正确解答的关键.

15. 某通信公司准备逐步在歌乐山上建设5G基站. 如图，某处斜坡的坡度（或坡比）为，通讯塔垂直于水平地面，在处测得塔顶的仰角为，在处测得塔顶的仰角为，斜坡路段长26米，则通讯塔的高度为（   ）（参考数据：）

A. 米    B. 米     C. 56米    D. 66米

【解答】如图，延长与水平线交于，过作，为垂足，过作，为垂足，连接，，

∵斜坡的坡度为，

∴

设米，则米，

在中，米，由勾股定理得，

，

即，

解得，

∴（米），（米），

∵斜坡的坡度为

设米，则米，

∵，

∴米，

∴米，

在中，米，米，

∵

∴，

解得，

∴（米），（米），

（米），

∴（米），

答：基站塔的高为米.

故选：B.

二. 填空题（共6小题）

16. 若反比例函数的图象经过点，则的值是      .
【分析】根据反比例函数图象上点的坐标特点可得，再解即可.
【解答】解：∵反比例函数的图象经过点，

∴，

解得：，

故答案为：.

【点评】此题主要考查了反比例函数图象上点的坐标特点，关键是掌握反比例函数图象上的点的横纵坐标的积是定值，即.

17. 某几何体的主视图、左视图和俯视图分别如图所示，则该几何体的表面积为   8π   .

【分析】由三视图可知，这个一个水平放置的圆柱，它的底面直径为2，高为3，根据圆柱的表面积计算公式即可解答.
【解答】解：由三视图可知，该几何体是一个圆柱体，其表面积

故答案为：8π.

【点评】本题主要考查由三视图判断几何体以及圆柱表面积的计算，熟练掌握圆柱表面积的计算公式是解题的关键

18. 反比例函数的图象如图所示，点在该函数图象上，垂直于轴，垂足为点，如果，那么      .

【分析】过双曲线上任意一点引轴、轴垂线，所得的面积为矩形面积的一半，即.
【解答】解：由于点在反比例函数的图象上，

则

又由于函数的图象在第二、四象限，故，

则，

故答案为：.

【点评】此题主要考查了反比例函数中的几何意义，即过双曲线上任意一点引轴、轴垂线，所得矩形面积为.

19. 如图，在平面直角坐标系中，点光源位于处，木杆两端的坐标分别为，. 则木杆在轴上的影长为   8   .

【分析】证明，然后利用相似比可求出的长.
【解答】解：∵木杆两端的坐标分别为，，

∴，

∴

∵，，.

∴

∴，

∴，

故答案为：8.

【点评】本题考查了中心投影：中心投影的光线特点是从一点出发的投射线，物体与投影面平行时的投影是放大（即位似变换）的关系.

20. 已知是锐角，，则   30   °.
【分析】利用特殊角的三角函数值，进行计算即可解答.
【解答】解：∵，

∴，

∴，

∴，

故答案为：30.

【点评】本题考查了特殊角的三角函数值，熟练掌握特殊角的三角函数值是解题的关键.

21. 如图，反比例函数的图象经过矩形对角线的交点和点，点、在轴上.

（1）若点的坐标是，则点的坐标是      ；

（2）若的面积为6，则   8   .

解答：解：（1）∵反比例函数的图象经过点，

∴，

∴，

∴，

∵是矩形对角线的交点，

∴点的纵坐标为2，

∴当时，，

∴点的坐标是.

故答案为：

（2）如图，过点作于，

设点，，

∵点是矩形的对角线的交点，

∴，

∵点在反比例函数的图象上，

∴，

∴，

∵的面积为6，

∴，

∴，

故答案为：8.

三. 解答题（共2小题）

22. 如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于点，.

（1）求一次函数和反比例函数的表达式；

（2）请根据函数图象直接写出关于的不等式的解；

（3）连接，，求的面积.

【分析】（1）利用待定系数法即可求得；

（2）通过观察图象即可求得；

（3）把三角形的面积看成是三角形和三角形的面积之和进行计算.
【解答】解：（1）∵点，在反比例函数的图象上，

∴，

∴

∴反比例函数表达式为，点的坐标为.

∵点和在一次函数的图象上，

∴，解得，

∴一次函数表达式为；

（2）由图象可知，关于的不等式的解为或；

（3）∵是直线与轴的交点，

∴当时，，

∴点.

∴.

∴

【点评】本题考查了用待定系数法确定反比例函数的比例系数，求出函数解析式；要能够熟练借助直线和轴的交点运用分割法求得不规则图形的面积. 同时间接考查函数的增减性，从而来解不等式.

23. 如图，一路灯距地面5. 6米，身高1. 6米的小方从距离灯的底部（点O）5米的处，沿所在的直线行走到点时，人影长度增长3米，求小方行走的路程.

【分析】利用身高与影长成正比可以求得的长，然后再利用相似三角形求得的长即可.
【解答】解：∵

∴，

∴，

∴，

∴

解得；

∵所在的直线行走到点时，人影长度增长3米，

∴，

同理可得，

∴，

即，

解得.

答：小方行走的路程为7. 5m.

【点评】本题考查的是相似三角形在实际生活中的中心投影应用，根据题意得出相似三角形，再利用相似三角形的对应边成比例求解是解答此题的关键.