2022-2023学年广东省清远市四校联盟高一上学期期中数学试题（解析版）

2022-2023学年第一学期“四校联盟”期中检测

高一数学试卷

考试时间：120分钟

一、单选题

1. 已知，则图中阴影部分表示的集合（    ）

A.  B.

C.  D.

【答案】A

【解析】

【分析】根据已知图可知阴影部分为两集合的公共部分.

【详解】由已知条件Venn图可知，阴影部分为两个集合的交集，则.

故选：A

2. 已知集合，则与集合A的关系为（    ）

A.  B. -1  C.  D.

【答案】C

【解析】

【分析】根据元素与集合之间的关系，即可得到答案.

【详解】由已知可得，-1是集合中的元素，根据元素与集合之间的关系，知.

故选：C.

3. 命题：，的否定形式为（    ）

A. ， B. ，

C. ， D. ，

【答案】D

【解析】

【分析】“任意一个都符合”的否定为“存在一个不符合”

【详解】由题意，“任意一个都符合”的否定为“存在一个不符合”，故为，.

故选：D

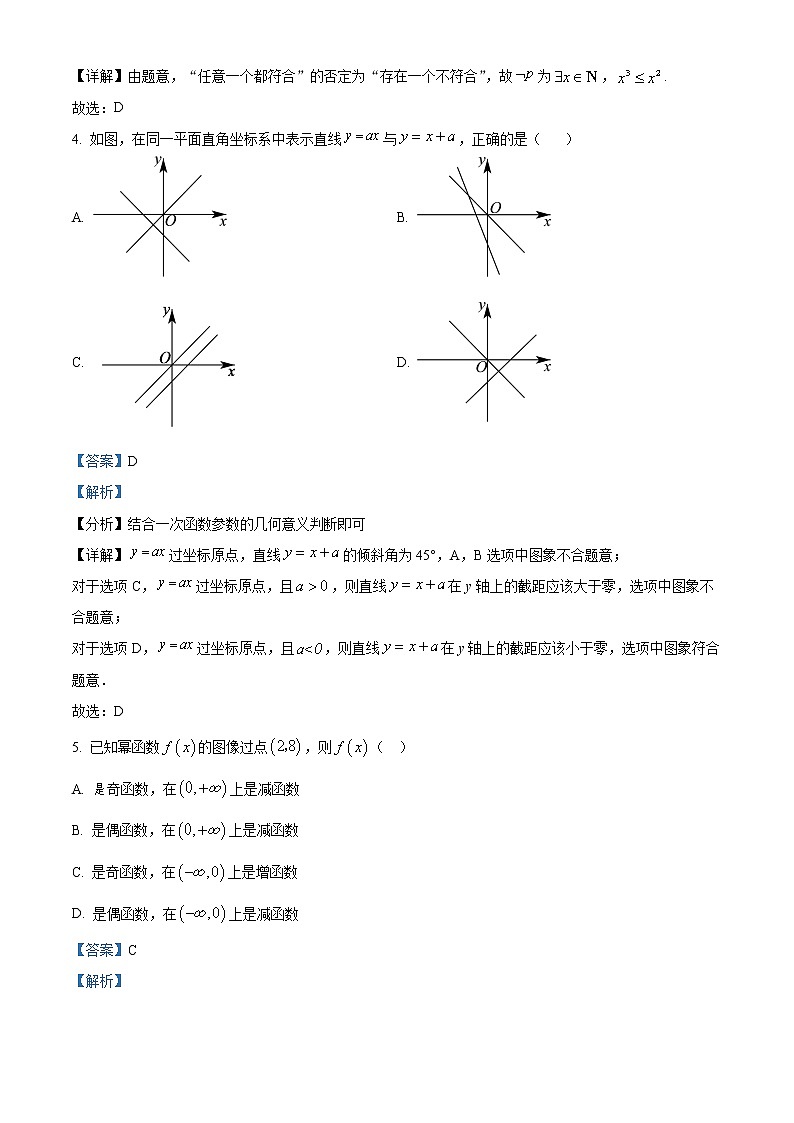
4. 如图，在同一平面直角坐标系中表示直线与，正确的是（    ）

A.  B.

C.  D.

【答案】D

【解析】

【分析】结合一次函数参数的几何意义判断即可

【详解】过坐标原点，直线的倾斜角为45°，A，B选项中图象不合题意；

对于选项C，过坐标原点，且，则直线在y轴上的截距应该大于零，选项中图象不合题意；

对于选项D，过坐标原点，且，则直线在y轴上的截距应该小于零，选项中图象符合题意．

故选：D

5. 已知幂函数的图像过点，则（    ）

A. 奇函数，在上是减函数

B. 是偶函数，在上是减函数

C. 是奇函数，在上是增函数

D. 是偶函数，在上是减函数

【答案】C

【解析】

【分析】由幂函数的图像过点，求出，从而根据幂函数的性质即可选出正确选项.

【详解】解：设幂函数解析式为，

因为幂函数的图像过点，

，解得，

则，

是奇函数，在上单调递增，

故选：C.

6. 若函数满足，，则下列判断错误的是（    ）

A.  B.

C. 图象的对称轴为直线 D. f（x）的最小值为－1

【答案】C

【解析】

【分析】根据已知求出，再利用二次函数的性质判断得解.

【详解】解：由题得，解得，，

所以，

因为，所以选项A正确；

所以，所以选项B正确；因为，所以选项D正确；

因为的对称轴为，所以选项C错误．

故选：C

7. 设，且，则（    ）

A.  B. 7 C. 17 D.

【答案】D

【解析】

【分析】根据f(x)＝ax3＋bx－5，可得g(x)＝f(x)＋5＝ax3＋bx为奇函数，根据f(－7)＝7，求出g(－7)的值，再根据奇函数的性质，求出g(7)的值，进而得到f(7)的值．

【详解】令g(x)＝f(x)＋5＝ax3＋bx，

∵g(－x)＝a(－x)3＋b(－x)＝－ax3－bx＝－g(x)，∴g(x)为奇函数，

∵f(－7)＝7，∴g(－7)＝f(－7)＋5＝12，

又∵g(－7)＝－g(7)，∴g(7)＝－12，

又∵g(7)＝f(7)＋5，∴f(7)＝－17，

故选：D．

8. 若，则下列不等式一定成立的是（    ）

A.  B.

C.  D.

【答案】C

【解析】

【分析】对A，B，C，D选项作差与0比较即可得出答案.

【详解】对于A，因为，故，即，故A错误；

对于B，，无法判断，故B错误；

对于C，因为，，故C正确；

对于D，因为，故，即，故D错误．

故选：C．

二、多选题

9. 下列四个结论中，正确的有（    ）

①；②；③⫋；④.

A. ① B. ② C. ③ D. ④

【答案】AC

【解析】

【分析】根据空集的定义和性质可得答案.

【详解】①空集是自身的子集，正确；0不是空集中的元素，②错误；空集是任何非空集合的真子集，③正确；是含一个元素0的集合，不是空集，④错误.

故选：AC.

10. 下列说法正确的有（    ）

A. 函数与函数是同一函数

B. 函数在定义域上是偶函数

C. 若，则在定义域内单调递减

D. 若，则函数的值域为

【答案】BD

【解析】

【分析】根据函数相等的两要素可判断A，根据奇偶性的定义判断B，根据幂函数的性质判断C，根据函数的定义判断D.

【详解】对于A，的定义域为，的定义域为，

定义域不相同，不是同一函数，所以A错误；

对于B，，定义域为，

，，

所以函数定义域上是偶函数，故B正确；

对于C，在单调递减，故C错误；

对于D，因为

所以值域为，故D正确.

故选：BD

11. 下列结论中正确的有（    ）

A. 若命题“，”为假命题，则实数的取值范围是

B. 若，则“”的充要条件是“”

C. “”是“”的充分不必要条件

D. 当时，的最小值为

【答案】ACD

【解析】

【分析】转化为，，计算，可得出的范围，即可判断A项；根据不等式的性质，可判断B项；求出的等价条件为或，即可判断C项；根据基本不等式，即可判断D项.

【详解】对于A项，等价于，，则，解得，故A项正确；

对于B项，因为，显然，，所以；因为，若，则，故B项不正确；

对于C项，，所以等价于，即，所以或.显然“”是“或”的充分不必要条件，故C项正确；

对于D项，当时，，当且仅当，即时，等号成立，故D项正确.

故选：ACD.

12. 已知函数，下列说法正确的是（    ）

A. 当时，的最小值为

B. 当时，，，有，则

C. 当时，，有，则

D. 当时，恒成立，则

【答案】AD

【解析】

【分析】根据二次函数的性质求出最小值可判断A；由题意可得，结合单调性求出最小值可判断B；由题意可得结合单调性求出最小值可判断C；由分析可知两个函数在上的零点相等即，整理可得代入，利用基本不等式求出最小值可判断D，进而可得正确选项.

【详解】对于A：当时，，的最小值为，故选项A正确；

对于B：当时，，若，，有，则，因为，所以时，所以，因为，在上单调递增，所以可得，故，故选项B不正确；

对于C：，有，则，

因为时，，当时，，所以，因为，在上单调递增，

所以可得，所以，故选项C不正确；

对于D：，因为，所以在上单调递增，且，所以当时，，当时，

，且的对称轴为，

令，则，，

所以当时，，

当时，，

若对于恒成立，则，即，

所以，所以，即，所以，

所以，当且仅当时等号成立，所以，故选项D正确；

故选：AD.

三、填空题

13. 设集合，．若，则实数a的值为______．

【答案】0

【解析】

【分析】根据，得到，然后结合集合中元素的互异性可得结果.

【详解】由题可知：，且

所以，得或1

当时，，不符合集合中元素的互异性

所以

故答案为：0

14. 已知命题p：，命题q：，那么p是q的______条件.（填“充分不必要”“必要不充分”“充要”“既不充分也不必要”）

【答案】必要不充分

【解析】

【分析】先化简命题，再利用充分条件和必要条件的定义判断.

【详解】解：因为命题p：，即为，命题q：即为，

所以p是q的必要不充条件，

故答案为：必要不充分

15. 已知不等式的解集是，则__________.

【答案】

【解析】

【分析】由题可知方程的解为或.后由韦达定理可得答案.

【详解】由题方程的解为或，则由韦达定理有：

，故

故答案为：

16. 函数的单调减区间为__________．

【答案】##

【解析】

【分析】由幂函数、二次函数的单调性及复合函数单调性的判断法则即可求解.

【详解】解：函数的定义域为，

令，，，

因为函数在上单调递增，在上单调递减，在上单调递增，

所以函数单调减区间为，单调增区间为.

故答案为：.

四、解答题

17. 已知全集，集合

（1）当时，求与；

（2）若，求实数a的取值范围.

【答案】（1），或   

（2）

【解析】

【分析】（1）根据集合的交并补的运算，即可求得答案；

（2）根据可得，讨论和，列出不等式，求得答案.

【小问1详解】

由可得，

所以，又当时，，

所以，

故或，

故或.

【小问2详解】

由题意,

当时，，可得；

当时， ，可得；

综上，.

18. 已知二次函数关于直线对称，，且二次函数的图像经过点（1，2）.

（1）求的解析式；

（2）求在上的值域.

【答案】（1）   

（2）

【解析】

【分析】（1）待定系数法设二次函数的解析式，根据题意联立方程组解出即可；

（2）利用二次函数的性质求二次函数在闭区间上的最值（或值域）.

【小问1详解】

设

由题意可得

解得

故.

【小问2详解】

由题可知函数的对称轴为

所以函数在区间上单调递减，在区间上单调递增

因为，，

所以函数在上的值域为.

19. 已知函数.

（1）判断在区间上的单调性，并用定义法证明.

（2）若对恒成立，求的取值范围.

【答案】（1）在区间上单调递增，证明见解析   

（2）.

【解析】

【分析】（1）利用函数的单调性定义证明；

（2）根据（1）的结论求得函数的最小值即可.

小问1详解】

解：在区间上单调递增，

设，，且，

则，

由，，得，，

又由，得，

于是，即，

所以在区间上单调递增；

【小问2详解】

由（1）知在区间上单调递增，

则当时，有最小值为1，

因为对恒成立，

所以，所以，

所以 的取值范围为.

20. 如图，某人计划用篱笆围成一个一边靠墙（墙的长度没有限制）的矩形菜园．设菜园的长为xm，宽为ym．

（1）若菜园面积为72m2，则x，y为何值时，可使所用篱笆总长最小？

（2）若使用的篱笆总长度为30m，求的最小值．

【答案】（1）菜园的长x为12m，宽y为6m时，可使所用篱笆总长最小   

（2）．

【解析】

【分析】（1）由已知可得xy＝72，而篱笆总长x+2y．利用基本不等式x+2y≥2即可得出；

（2）由已知得x+2y＝30，利用基本不等式（）•（x+2y）＝55+2，进而得出．

【小问1详解】

由已知可得xy＝72，而篱笆总长为x+2y．又∵x+2y≥224，

当且仅当x＝2y，即x＝12，y＝6时等号成立．

∴菜园的长x为12m，宽y为6m时，可使所用篱笆总长最小．

【小问2详解】

由已知得x+2y＝30，

又∵（）•（x+2y）＝55+29，

∴，当且仅当x＝y，即x＝10，y＝10时等号成立．

∴的最小值是．

21. 已知函数

（1）若，求实数a的值；

（2）若，求实数m的取值范围．

【答案】（1）或；   

（2）.

【解析】

【分析】（1）根据，分，和三种情况讨论即可得出答案；

（2）分，和三种情况讨论，解不等式即可.

【小问1详解】

解：①当时，，

解得，不合题意，舍去；

②当时，，即，

解得或，

因为，，所以符合题意；

③当时，，

解得，符合题意；

综合①②③知，当时，或；

【小问2详解】

解：由，

得或或，

解得或，

故所求m的取值范围是.

22. 已知函数．

（1）若函数在区间上具有单调性，求实数的取值范围；

（2）求函数在区间上的最小值.

【答案】（1）   

（2）

【解析】

【分析】（1）要使函数在上具有单调性，则函数图象的对称轴不在这个区间内即可；

（2）函数上分单调递减、单调递增、不单调三种情况讨论，求最小值即可.

【小问1详解】

因为函数图象的对称轴为，

所以要使函数在上具有单调性，

则，即

或，即

则的取值范围为；

【小问2详解】

①若函数在上单调递减，则，即，此时函数在区间上的最小值为；

②若函数在上单调递增，则，即，此时函数在区间上的最小值为；

③若函数在上不单调，则，即，此时函数在区间上的最小值为，

综上所述，函数在区间上的最小值为

.