初中数学北师大版七年级下册第一章 整式的乘除7 整式的除法获奖ppt课件

这是一份初中数学北师大版七年级下册第一章 整式的乘除7 整式的除法获奖ppt课件，文件包含172多项式除单项式pptx、172多项式除单项式教学设计docx等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。

1、单项式除以单项式的步骤：①系数相除②同底数幂相除③对于只在被除式里含的字母，则连同它的指数一起作为商的一个因式
2、练一练（1）6a3÷2a2= . （2）-8a3b2÷2ab= . （3）-8a3b2c2 ÷(-2ab）= .
1.若一个长方形的长为a+b，宽为m， 则它的面积是 。2.若一个长方形的面积为am + bm， 宽为m， 则它的长是 。
（a+b）∙m=am + bm
（am+bd)÷m=a + b
想一想：用什么方法可以得出答案。
计算下列各题，说说你的理由.
（1）(ad + bd)÷d =____________;
（2）(a2b + 3ab)÷a =__________;
（3）(xy3－2xy)÷xy =__________.
如何进行多项式除以单项式的运算？
(am + bm + cm)÷m= am÷m + bm÷m + cm÷m= a + b + c
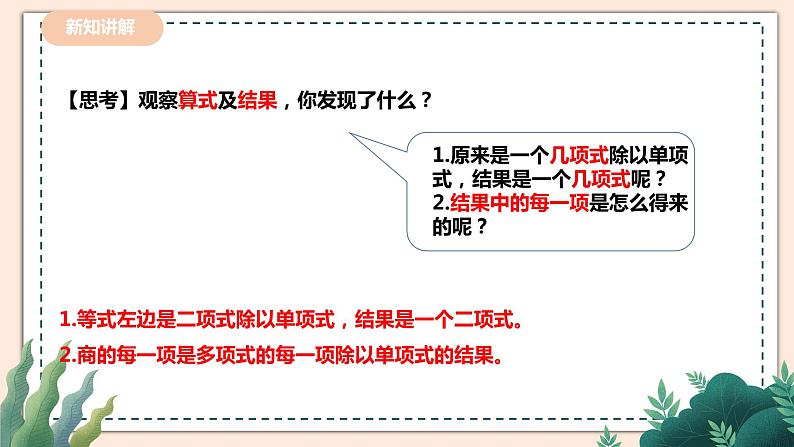
【思考】观察算式及结果，你发现了什么？
1.等式左边是二项式除以单项式，结果是一个二项式。2.商的每一项是多项式的每一项除以单项式的结果。
1.原来是一个几项式除以单项式，结果是一个几项式呢？2.结果中的每一项是怎么得来的呢？
多项式除以单项式的法则
多项式除以单项式，先用这个多项式的 除以这个 ，再把所得的商 .
关键： 应用法则是把多项式除以单项式转化为单项式除以单项式.
（1）(6ab + 8b)÷2b；
（2）(27a3－15a2 + 6a)÷3a；
（3）(9x2y－6xy2)÷3xy；
解：（1）(6ab + 8b)÷2b
= 6ab ÷2b + 8b÷2b
（2）(27a3－15a2 + 6a)÷3a
= 27a3 ÷3a－15a2 ÷3a + 6a÷3a
= 9a2 －5a + 2
（3）(9x2y－6xy2)÷3xy
= 9x2y ÷3xy －6xy2÷3xy
总结：多项式除以单项式中的“数的变化特点”.我（1）项数：被除式有几项，则商就有几项，计算中不可漏项；（2）系数：各项系数相除时，应包含前面的符号 （小技巧：先确定系数的符号再进行其他运算）
已知一个多项式除以2x2，所得的商是2x2＋1，余式是3x－2，请求出这个多项式．
解：根据题意得 2x2(2x2＋1)＋3x－2 ＝4x4＋2x2＋3x－2， 则这个多项式为4x4＋2x2＋3x－2.
解：设下山时所用时间为 t3
1．计算(8a2b3－2a3b2＋ab)÷ab的结果是(　　)A．8ab2－2a2b＋1 B．8ab2－2a2bC．8a2b2－2a2b＋1 D．8ab－2a2b＋1
2．计算(－81xn＋5＋6xn＋3－3xn＋2)÷(－3xn－1)等于(　　)A．27x6－2x4＋x3 B．27x6＋2x4＋xC．27x6－2x4－x3 D．27x4－2x2－x
3.一个矩形的面积为a2＋2a，若一边长为a，则其邻边长为________．4.计算多项式－2x(3x－2)2＋3除以3x－2后，所得商式与余式两者之和为
(1) (3xy+y) ÷y
解：原式=3xy÷y+y÷y
(2) (12a3b2-6a2)÷3a
解：原式=12a3b2÷3a+(－6a2)÷3a
=4a2b2+(－2a)
(3) (12a3b2-6a2)÷(-3a)
解：原式=12a3b2÷(-3a)+(－6a2)÷(-3a)
1.课本第31页习题1.14第1、3题
用这个多项式的每一项除以这个单项式，再把所得的商相加.
1.计算时，多项式的各项要包括它们前面的符号，要注意符号的变化；2.当被除式的项与除式的项相同时，商是1，不能把“1”漏掉.