苏科版八年级下册9.3 平行四边形课堂教学ppt课件

这是一份苏科版八年级下册9.3 平行四边形课堂教学ppt课件，共18页。PPT课件主要包含了平行四边形的判定，温故知新，画图思考，共同探究，讨论交流，判定运用，总结归纳，对角线，反证法，类比的思想方法等内容，欢迎下载使用。

(1) 两组对边分别平行的四边形叫做平行四边形.（定义）(2)一组对边平行且相等的四边形是平行四边形。（定理） (3) 两组对边分别相等的四边形是平行四边形。 （定理）
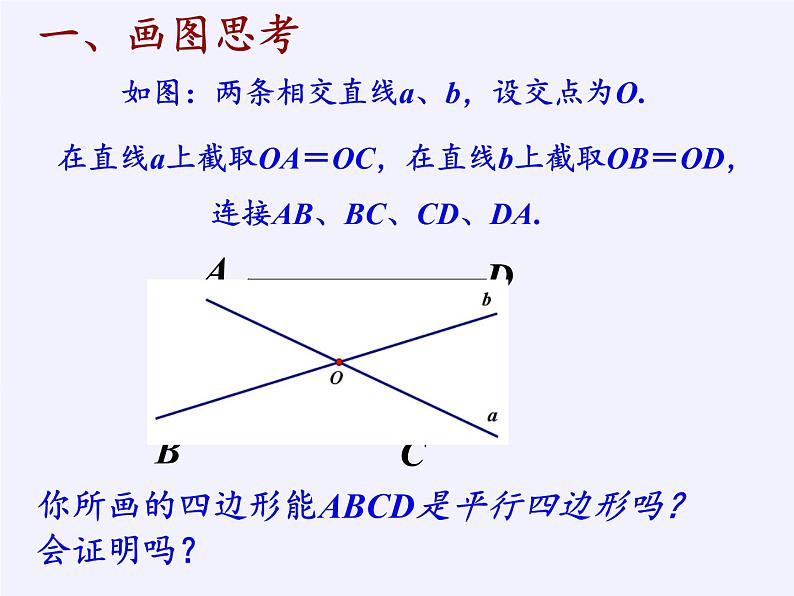
　如图：两条相交直线a、b，设交点为O.　　在直线a上截取OA＝OC，在直线b上截取OB＝OD，连接AB、BC、CD、DA.
你所画的四边形能ABCD是平行四边形吗？会证明吗？
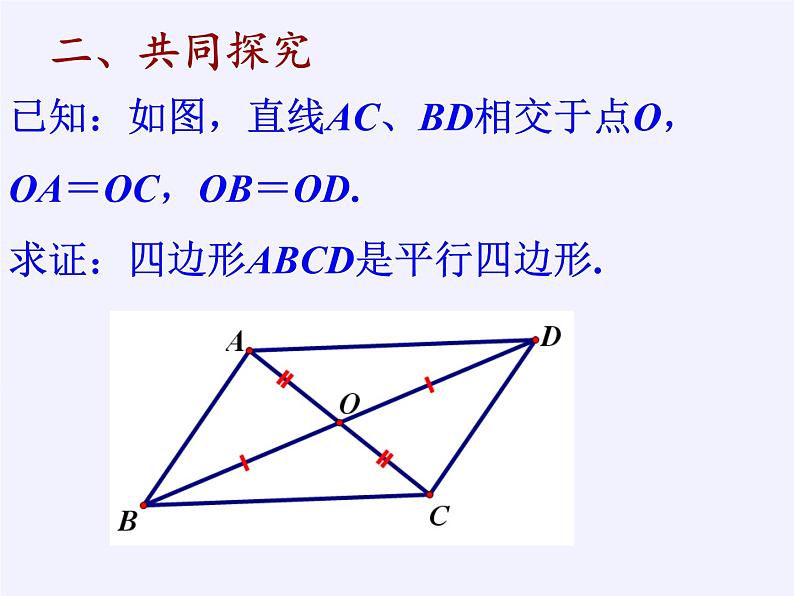
已知：如图，直线AC、BD相交于点O，OA＝OC，OB＝OD.求证：四边形ABCD是平行四边形.
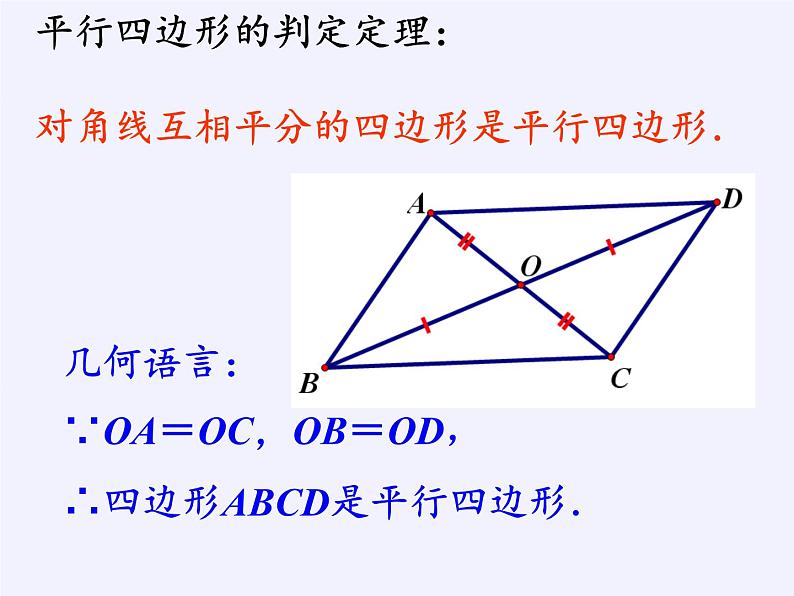
平行四边形的判定定理：对角线互相平分的四边形是平行四边形．
几何语言：∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形．
这种推理方法叫做反证法
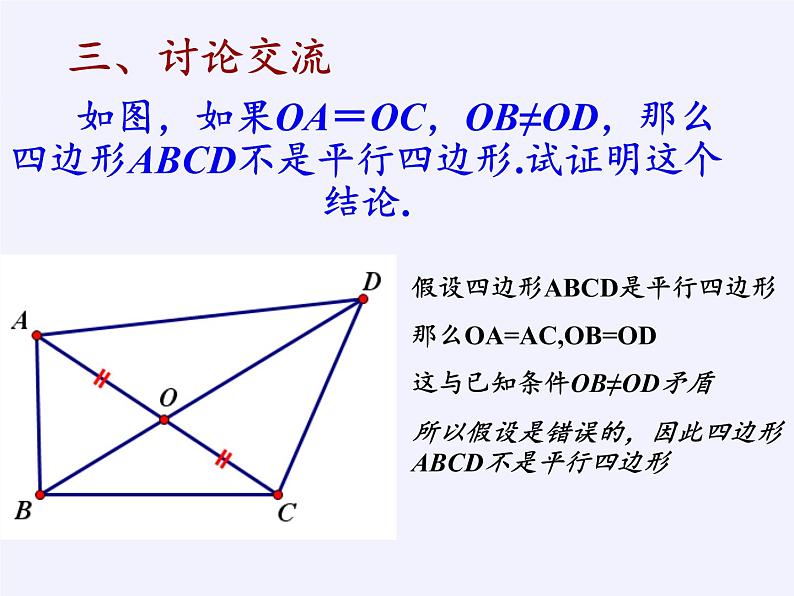
　　如图，如果OA＝OC，OB≠OD，那么四边形ABCD不是平行四边形.试证明这个结论.
假设四边形ABCD是平行四边形那么OA=AC,OB=OD这与已知条件OB≠OD矛盾所以假设是错误的，因此四边形ABCD不是平行四边形
先提出与结论相反的假设，然后由这个“假设”出发推导出与已知条件矛盾，或与基本事实、定义、定理矛盾，说明“假设”是错误的，因而命题的结论成立，这种证明的方法称为 反证法。
例1：已知：如图在□ABCD中，对角线AC与BD交于O点，已知点E、 F分别是OA、OC的中点。求证：四边形BEDF是平行四边形。
　变式1：已知：如图，在□ABCD中，点E、F在AC上，且AE＝CF.求证：四边形BEDF是平行四边形．
变式2:已知：如图,在□ABCD中，在直线AC上分别截取AE、CF，且AE=CF，求证：四边形BEDF是平行四边形。
变式3：已知：如图在□ABCD中，对角线AC与BD交于O点，已知点E、G、F、H分别是AO、OC 、BO 、DO的中点。 求证：四边形EFGH是平行四边形。
变式4:已知：如图在□ABCD中，对角线AC与BD交于O点，直线EF经过O点,交边AD、BC与点E、F。求证：(1)△AOE≌△COF (2)四边形BEDF是平行四边形。
变式5：已知：如图在□ABCD中，对角线AC与BD交于O点，F、H分别是OB、OD的中点，直线EG经过O点,交边AD、BC与点E、G。 求证：四边形EFGH是平行四边形。
当所证明四边形与原平行四边形有一条公共的对角线或彼此的一条对角线在同一条直线上时，往往从对角线上解题较容易！
(1) 两组对边分别平行的四边形叫做 平行四边形.(定义) (2) 两组对边分别相等的四边形是 平行四边形。（定理） (3)一组对边平行且相等的四边形是 平行四边形。 （定理） (4)两条对角线互相平分的四边形是 平行四边形。 （定理）
1.平行四边形的判定方法
通过本节课学习你会什么收获？