










七数湘教版下册 4.1 平面上两条直线的位置关系 PPT课件+教案+练习
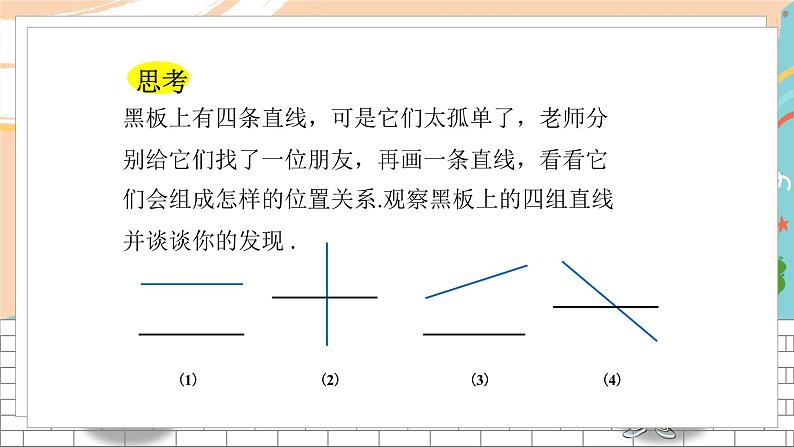
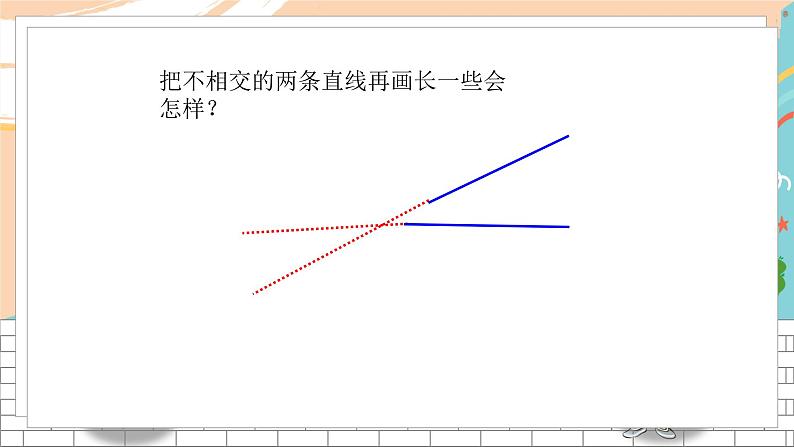
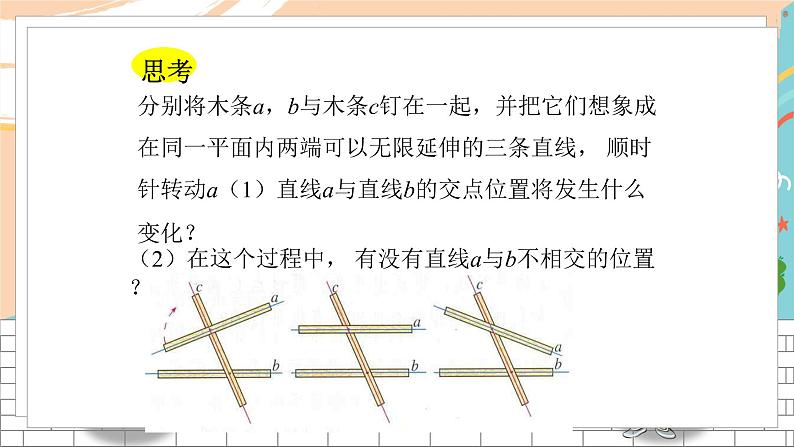
展开4.1 平面上两条直线的位置关系
一.选择题(共5小题)
1.a,b,c为同一平面内的任意三条直线,那么它们的交点可能有( )个.
A.1,2或3 B.0,1,2或3 C.1或2 D.以上都不对
2.下列选项中正确的是( )
A.相等的角是对顶角
B.两直线平行,同旁内角相等
C.直线外一点到这条直线的垂线段,叫点到直线的距离
D.经过直线外一点,有且只有一条直线与这条直线平行
3.图中,∠1、∠2是对顶角的为( )
A. B.
C. D.
4.对于同一平面内的三条直线a,b,c,下列命题中不正确的是( )
A.若a∥b,b∥c,则a∥c B.若a⊥b,a⊥c,则b⊥c
C.若a∥b,a⊥c,则b⊥c D.若a⊥b,a⊥c,则b∥c
5.下列各图中,∠1和∠2是对顶角的是( )
A. B.
C. D.
二.填空题(共5小题)
6.如图,直线AB、CD、EF交于点O.
(1)∠COE的对顶角是 .
(2)∠AOF的对顶角是 .
(3)∠BOF的邻补角是 .
(4)∠BOE的邻补角是 .
(第6题图)
7.观察下列图形,并阅读,图形下面的相关字.
(第7题图)
两条直线相交最多有1个交点 三条直线相交最多有3个交点 四条直线相交最多有6个 交点
则n条直线最多有 个交点.
8.同一平面内的5条直线两两相交,最多有 个交点,最多把平面分成 个部分,最多构成 对对顶角.
9.如图,直线AB,CD相交于点O,若∠BOD=∠BOD+18°,则∠AOD= .
(第9题图)
10.如图所示,其中共有 对对顶角.
(第10题图)
三.解答题(共4小题)
11.如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)填空:∠AOC=50°,∠FOD= 度;
(2)∠AOC=α°.则∠EOD= (用含α的式子表示);
(3)探究∠EOD与∠FOD的数量关系,并说明理由.
(第11题图)
12.(合作探究题)在同一平面内三条直线交点有多少个?
甲:同一平面三直线相交交点的个数为0个,因为a∥b∥c,如图(1)所示.
乙:同一平面内三条直线交点个数只有1个,因为a,b,c交于同一点O,如图(2)所示.
以上说法谁对谁错?为什么?
(第12题图)
13.(原创题)如图所示,在∠AOB内有一点P.
(1)过P画l1∥OA;(2)过P画l2∥OB;
(3)用量角器量一量l1与l2相交的角与∠O的大小有怎样关系?
(第13题图)
14.探索研究:
A:观察如图所示中的各图,寻找对顶角(不含平角):
(第14题图)
(1)如图a,图中共有 对不同对顶角;
(2)如图b,图中共有 对不同的对顶角;
(3)如图c,图中共有 对不同的对顶角;
(4)研究(1)﹣(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 对对顶角;
(5)计算2013条直线相交于一点,则可形成 对对顶角.
B:
(1)3条直线两两相交最多有 个交点,此时有 对不同的对顶角;
(2)4条直线两两相交最多有 个交点,此时有 对不同的对顶角;
(3)n条直线两两相交最多有 个交点,此时有 对不同的对顶角;
(4)计算2013条直线最多有 个交点,则可形成 对不同的对顶角,那么2013条直线最多形成 对不同的对顶角.
参考答案
一.1.B 2.D 3.C 4.B 5.D
二. 6.∠DOF;∠BOE;∠AOF和∠BOE;∠AOE和∠BOF.
7. 8. 10;16;20 9. 144° 10.4
三.11.解:(1)∵∠AOC=50°,
∴∠BOD=∠AOC=50°,
∵OF平分∠BOD,
∴∠FOD=;
(2)∵OE平分∠AOD,
∴∠EOD=,
∵∠AOD=180°﹣∠AOC=(180﹣α)°,
∴∠EOD=(180﹣α)°=(90﹣α)°.
(3)∠EOD+∠FOD=90°,
理由:∵OE平分∠AOD,OF平分∠BOD,
∴∠DOE=∠AOD,∠DOF=∠BOD,
∵∠BOD+∠AOD=180°,
∴∠DOE+∠DOF=(∠BOD+∠AOD)=90°.
12.解:甲、乙说法都不对,都少了三种情况.a∥b,c与a,b相交如答图(1);
a,b,c两两相交如答图(2),所以三条直线互不重合,交点有0个或1个或2个或3个,共四种情况.
(第12题答图)
13.解:(1)(2)如答图.
(3)l1与l2夹角有两个:∠1,∠2;∠1=∠O,∠2+∠O=180°,所以l1和l2的夹角与∠O相等或互补.
(第13题答图)
14. A.解:(1)有2对对顶角;
(2)有6对对顶角;
(3)有12对对顶角;
(4)有n条直线时,有n(n﹣1)对对顶角;
(5)n=2013时,可形成2013×2012=4050156对顶角.
B解:(1)如答图(1),可得三条直线两两相交,最多有3个交点;有6对对顶角.
(2)如图(2),可得四条直线两两相交,最多有6个交点;又12对对顶角.
(3)由(1),得=3,
由(2),得=6;
∴可得,n条直线两两相交,最多有个交点(n为正整数,且n≥2).有n(n﹣1)对对顶角.
(第14题答图)
(4)当n=2013时,有2025078个交点,有4050156对对顶角.









