武汉市各区2020-2021学年七下数学期中第24题压轴题汇编(word版含解析)
展开武汉市各区2020-2021七下数学期中第24题压轴题汇编
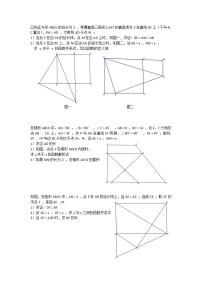
1.(2021春•青山区期中)已知A、B两点的坐标分别为A(﹣2,1),B(﹣4,﹣1),将线段AB水平向右平移到DC,连接AD,BC,得四边形ABCD,且S四边形ABCD=12.
(1)点C的坐标为 ,点D的坐标为 ;
(2)如图1,CG⊥x轴于G,CG上有一动点Q,连接BQ、DQ,求BQ+DQ最小时Q点位置及其坐标,并说明理由;
(3)如图2,E为x轴上一点,若DE平分∠ADC,且DE⊥HC于E,∠ABH=14∠ABC.求∠BHC与∠A之间的数量关系.
2.(2021春•江汉区期中)如图,在平面直角坐标系中,直线AB与坐标轴交于A(﹣4,0),B(0,m)两点,点C(2,3),P(−32,n)在直线AB上.我们可以用面积法求点B的坐标.
(1)请阅读并填空:
一方面,过点C作CN⊥x轴于点N,我们可以由A,C的坐标,直接得出三角形AOC的面积为 平方单位;
另一方面,过点C作CQ⊥y轴于点Q,三角形AOB的面积=12BO•AO=2m2,三角形BOC的面积= 平方单位.
∵三角形AOC的面积=三角形AOB的面积+三角形BOC的面积,
∴可得关于m的一元一次方程为 ,解这个方程,可得点B的坐标为 .
(2)如图,请你仿照(1)中的方法,求点P的纵坐标.
(3)若点H(3,h),且三角形ACH的面积等于24平方单位,
请直接写出h的值.
3.(2021春•汉阳区期中)如图1在平面直角坐标系中,大正方形OABC的边长为m厘米,小正方形ODEF的边长为n厘米,且|m﹣4|+n−2=0.
(1)求点B、点D的坐标.
(2)起始状态如图1所示,将大正方形固定不动,小正方形以1厘米/秒的速度沿x轴向右平移,如图2.设平移的时间为t秒,在平移过程中两个正方形重叠部分的面积为S平方厘米.
①当t=1.5时,S= 平方厘米;
②在2≤t≤4这段时间内,小正方形的一条对角线扫过的图形的面积为 平方厘米;
③在小正方形平移过程中,若S=2,则小正方形平移的时间t为 秒.
(3)将大正方形固定不动,小正方形从图1中起始状态沿x轴向右平移,在平移过程中,连接AD,过D点作DM⊥AD交直线BC于M,∠DAx的角平分线所在直线和∠CMD的角平分线所在直线交于N(不考虑N点与A点重合的情形),求∠ANM的大小并说明理由.
4.(2021春•硚口区期中)已知A(0,a)、B(b,0),且a−5+(b﹣4)2=0.
(1)直接写出点A、B的坐标;
(2)点C为x轴负半轴上一点满足S△ABC=15.
①如图1,平移直线AB经过点C,交y轴于点E,求点E的坐标;
②如图2,若点F(m,10)满足S△ACF=10,求m.
(3)如图3,D为x轴上B点右侧的点,把点A沿y轴负半轴方向平移,过点A作x轴的平行线l,在直线l上取两点G、H(点H在点G右侧),满足HB=8,GD=6.当点A平移到某一位置时,四边形BDHG的面积有最大值,直接写出面积的最大值.
5.(2021春•武昌区期中)在平面直角坐标系中,点A(a,1),B(b,3)满足关系式(a+1)2+|b﹣2|=0.
(1)求a、b的值;
(2)若点P(3,n)满足△ABP的面积等于6,求n的值;
(3)线段AB与y轴交于点C,动点E从点C出发,在y轴上以每秒1个单位长度的速度向下运动,动点F从点M(﹣8,0)出发,以每秒2个单位长度的速度向右运动,问t为何值时有S△ABE=2S△ABF?请直接写出t的值.
6.(2021春•官渡区期末)如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足a−2b+|b﹣2|=0.
(1)则C点的坐标为 ;A点的坐标为 .
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.AC的中点D的坐标是(1,2),设运动时间为t(t>0)秒.问:是否存在这样的t,使S△ODP=S△ODQ?若存在,请求出t的值;若不存在,请说明理由
(3)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,∠OHC+∠ACE∠OEC的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
7.(2021春•黄陂区期中)在平面直角坐标系中,点A(m,n)满足n=m−4−4−m+m.
(1)直接写出点A的坐标;
(2)如图1,将线段OA沿y轴向下平移a个单位后得到线段BC(点O与点B对应),过点C作CD⊥y轴于点D,若4OD=3BD,求a的值;
(3)如图2,点E(0,5)在y轴上,连接AE,将线段OA沿y轴向上平移3个单位后得到线段FG(点O与点F对应),FG交AE于点P,y轴上是否存在点Q,使S△APQ=6,若存在,请求Q点的坐标;若不存在,请说明理由.
8.(2021春•武昌区期中)在平面直角坐标系中(单位长度为1cm),已知点A(0,m),N(n,0),且m−4+|m+n﹣10|=0.
(1)m= ,n= .
(2)如图,若点E是第一象限内的一点,且EN⊥x轴,过点E作x轴的平行线a,与y轴交于点A,点P从点E处出发,以每秒2cm的速度沿直线a向左移动,点Q从原点O同时出发,以每秒1cm的速度沿x轴向右移动.
①经过几秒PQ∥y轴?
②若某一时刻以A、O、Q、P为顶点的四边形的面积是10cm2,求此时点P的坐标.
9.(2021春•江岸区期中)如图,平面直角坐标系中,A(a,0),B(0,b),C(0,c),a+4+|2﹣b|=0,c=12(a﹣b).
(1)求△ABC的面积;
(2)如图2,点A以每秒m个单位的速度向下运动至A′,与此同时,点Q从原点出发,以每秒2个单位的速度沿x轴向右运动至Q′,3秒后,A′、C、Q′在同一直线上,求m的值;
(3)如图3,点D在线段AB上,将点D向右平移4个单位长度至E点,若△ACE的面积等于14,求点D坐标.
10.(2021春•洪山区期中)如图1,已知在平面直角坐标系中,点A(﹣4,0),点B(0,3),将线段AB向右平移4个单位长度至OC的位置,连BC.
(1)直接写出点C的坐标 ;
(2)如图2,过点C作CD⊥x轴于点D,在x轴正半轴有一点E(1,0),过点E作x轴的垂线EF交BC于F,动点P从F点开始,以每秒1个单位长度的速度沿射线FE运动,设运动的时间为t(秒),连接AC.
①试问:△PCD的面积是否为定值?若是,求出定值;若不是,请说明理由;
②当△PCA的面积为332时,求t的值及此时点P的坐标.
2参考答案与试题解析
一.解答题(共10小题)
1.【解答】解:(1)由平移可知,AB∥CD,且AB=CD,
∴四边形ABCD是平行四边形,
∵S四边形ABCD=12,
∴BC•|yA﹣yB|=12,
又∵A(﹣2,1),B(﹣4,﹣1),
∴BC×2=12,
解得BC=6,
∴C(2,﹣1),D(4,1),
故答案为:(2,﹣1),(4,1);
(2)连接BD交CG于Q',
由两点间线段最短可知,当B、D、Q三点共线时BQ+DQ最小,
即Q在Q'位置时BQ+DQ最小,
由题知,直线CG的解析式为:x=2,
设直线BD的解析式为y=kx,
代入D点坐标得4k=1,
解得k=14,
∴直线BD的解析式为:y=14x,
∵Q'是直线CG和直线BD的交点,
∴x=2y=14x,
解得x=2y=12,
∴Q'(2,12);
(3)设CH交AD于F,BH交AD于P,
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=180°﹣∠A,
∵DE平分∠ADC,DE⊥HC,
∴DC=DF,
∴∠CFD=∠DCF=12(180°﹣∠ADC)=12∠A,
∵∠ABH=14∠ABC,
∴∠ABH=14(180°﹣∠A),
∴∠APB=180°﹣∠A﹣∠ABH=135°−34∠A,
∴∠BPF=180°﹣∠APB=45°+34∠A,
∵∠PFH=∠CFD=12∠A,
∴∠BHC=∠BPF﹣∠PFH=45°+34∠A−12∠A=45°+14∠A,
即∠BHC=45°+14∠A.
2.【解答】解:(1)过点C作CN⊥x轴于点N,
∵A(﹣4,0),B(0,m),点C(2,3),
∴S△AOC=12×OA×CN=12×4×3=6(平方单位).
过点C作CQ⊥y轴于点Q,S△AOB=12BO•AO=2m(平方单位),S△BOC=m(平方单位).
∵S△AOC=S△AOB+S△BOC,
∴6=2m+m,
解得,m=2,
∴点B的坐标为(0,2).
故答案为:6,m,6=2m+m,(0,2).
(2)如图,连接OP,过点P作PE⊥OA于E,PF⊥OB于F.
∵S△AOB=S△AOP+S△POB,
∴12×4×2=12×4×n+12×2×32,
∴n=54,
∴点P的纵坐标为54.
(3)如图,过点H作x轴的垂线交AC于R.
设R(3,t),则有12×4×t=12×4×2+12×2×3,
解得t=3.5,
∴R(3,3.5),
当点H在直线AC的下方时,由S△ACH=S△ARH﹣S△CHR,
可得,24=12×(3.5﹣h)×7+12×1×(3.5﹣h),
解得h=﹣4.5,
当点H在直线AC的上方时,同法可得24=12×(h﹣3.5)×7+12×1×(h﹣3.5),
解得h=11.5.
综上所述,h的值为﹣4.5或11.5.
3.【解答】解:(1)∵|m﹣4|+n−2=0.
∴n=2,m=4,
∴B(4,4),D(0,2),
(2)①当T=1.5时,小正方形向右移动1.5cm,
S=2×1.5=3cm2;
②如图1所示,小正方形的一条对角线扫过的面积为红色平行四边形,
面积为2×2=4cm2;
③如图2,小正方形平移距离为4+1=5cm,
∴小正方形平移的距离为1cm或5cm,
∴t=1或5.
综上所述,小正方形平移的时间为1或5秒,
(3)如图3,过D作DQ∥x轴,过N作NP∥x轴,
∵MN平分∠CMD,
∴设∠CMG=∠DMG=y,则∠PNM=∠NMB=y,
∠MDQ=∠CMD=2y,
∵DM⊥AD,
∴∠ADQ=∠OAD=90°﹣2y,
∴∠DAx=180°﹣∠OAD=180°﹣(90°﹣2y)=90°+2y,
∵AN平分∠DAx,
∴∠NAx=12∠DAx=45°+y=∠PNA,
∴∠ANM=∠PNA﹣∠PNM=45°+y﹣y=45°.
4.【解答】解:(1)∵a−5+(b−4)2=0,且a−5≥0,(b﹣4)2≥0,
∴a﹣5=0,b﹣4=0,
解得:a=5,b=4,
∴A(0,5),B(4,0);
(2)①连接BE,如图1,
∵S△ABC=12×OA×BC=12×|yA|×BC=12×5×BC=15,
∴BC=6,
∴C(﹣2,0),
∵AB∥CE,
∴S△ABC=S△ABE,
∴12AE×4=15,
∴AE=152,
∴OE=52,
∴E(0,−52);
②∵F(m,10),
∴点F在过点G(0,10)且平行于x轴的直线l上,
延长CA交直线l于点H(a,10),过点H作HM⊥x轴于点M,则M(a,0),如图2,
∵S△HCM=S△ACO+S梯形AOMH,
∴12(a+2)×10=12×2×5+12×(5+10)⋅a,
解得:a=2,
∴H(2,10),
∵S△AFC=S△CFH﹣S△AFH,
∴12FH⋅(10−5)=10,
∴FH=4,
∵H(2,10),
∴F(﹣2,10)或(6,10),
∴m=﹣2或6;
(3)平移GH到DM,连接HM,则GD∥HM,GD=HM,如图3,
四边形BDHG的面积=△BHM的面积,
当BH⊥HM时,△BHM的面积最大,其最大值=12BH⋅HM=12BH⋅GD=12×8×6=24.
5.【解答】解:(1)∵(a+1)2+|b﹣2|=0,
∴a+1=0,b﹣2=0,
∴a=﹣1,b=2;
(2)如右图,过P作直线l垂直于x轴,延长AB交直线l于点Q,设Q的坐标为(3,m),
过A作AH⊥l交直线l于点H,
∵S△AHQ=S△ABH+S△BQH,
∴12×4(m﹣1)=12×(3+1)×(3﹣1)+12(m﹣1)(3﹣2),
解得m=113,
∴Q(3,113),
∵S△ABP=S△AQP﹣S△BPQ=12PQ×(3+1)−12PQ×(3﹣2)=32PQ,
又∵点P(3,n)满足△ABP的面积等于6,
∴32|n−113|=6,
解得n=233或−13;
(3)如图2,延长BA交x轴于D,过A作AG⊥x轴于G,过B作BN⊥x轴于N,
∵S梯形AGOC+S梯形CONB=S梯形AGNB,
∴12(1+OC)×1+12(OC+3)×2=12×(1+3)×3,
解得OC=53,
∴C(0,53),
∵S△ADG+S梯形AGNB=S△DNB,
∴12DG×1+12×(1+3)×3=12(DG+3)×3,
解得DG=32,
∵G(﹣1,0),
∴D(−52,0),
由题知,当t秒时,F(﹣8+2t,0),
∴DF=|﹣8+2t﹣(−52)|=|2t−112|,
∵CE=t,
∴S△ABE=12CE×[2﹣(﹣1)]=32t,S△ABF=S△BDF﹣S△DAF=12DF×(3﹣1)=|2t−112|,
∵S△ABE=2S△ABF,
∴32t=2|2t−112|,
解得t=225或2.
6.【解答】解:(1)∵a−2b+|b﹣2|=0,
∴a﹣2b=0,b﹣2=0,
解得a=4,b=2,
∴A(0,4),C(2,0);
(2)由条件可知:P点从C点运动到O点时间为2秒,Q点从O点运动到A点时间为2秒,
∴0<t≤2时,点Q在线段AO上,
即 CP=t,OP=2﹣t,OQ=2t,AQ=4﹣2t,
∴S△DOP=12OP⋅yD=12(2−t)×2=2−t,S△DOQ=12OQ⋅xD=12×2t×1=t,
∵S△ODP=S△ODQ,
∴2﹣t=t,
∴t=1;
(3)∠OHC+∠ACE∠OEC的值不变,其值为2.
∵∠2+∠3=90°,
又∵∠1=∠2,∠3=∠FCO,
∴∠GOC+∠ACO=180°,
∴OG∥AC,
∴∠1=∠CAO,
∴∠OEC=∠CAO+∠4=∠1+∠4,
如图,过H点作AC的平行线,交x轴于P,则∠4=∠PHC,PH∥OG,
∴∠PHO=∠GOF=∠1+∠2,
∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,
∴∠OHC+∠ACE∠OEC=∠1+∠2+∠4+∠4∠1+∠4=2(∠1+∠4)∠1+∠4=2.
7.【解答】解:(1)∵点A(m,n)满足n=m−4−4−m+m.
∴m﹣4≥0,4﹣m≥0,
∴m=4,
∴n=4=2,
∴A(4,2).
(2)∵将线段OA沿y轴向下平移a个单位后得到线段BC,A(4,2),
∴B(0,﹣a),C(4,2﹣a),D(0,2﹣a),
∴OD=|2﹣a|,BD=2,
①当点D位于x轴上方时,
∵4OD=3BD,
∴4(2﹣a)=3×2,
解得a=12;
②当点D位于x轴下方时,
∵4OD=3BD,
∴4(a﹣2)=3×2,
解得a=72.
综合以上可得a=12或72;
(3)连接AG,过点P作x轴的平行线,交AG于点M,交y轴于点N,
由题意有AG=3,EF=2,MN=4,EO=5,
∴S△EPF=12EF•PN=PN,S△APG=12AG•PM=32(4﹣PN),
∴S四边形AGFO=3×4=12,S△AEO=12×5×4=10,
∴S四边形AGFO﹣S△AEO=S△APG﹣S△PEF=2,
即32(4﹣PN)﹣PN=2,
解得PN=85,
设Q(0,n),EQ=|5﹣n|,
∴S△APQ=S△AEQ﹣S△AEQ=12EQ⋅MN−12EQ•PN=6,
即12EQ⋅(MN−PN)=12×125×EQ=6,
解得EQ=5,
即|5﹣n|=5,
解得n=0或n=10,
综合以上可得点Q的坐标为(0,0)或(0,10).
8.【解答】解:(1)依题意,得 m−4=0m+n−10=0,
解得m=4n=6;
故答案为:4,6;
(2)①设经过x秒PQ平行于y轴,
依题意,得6﹣2x=x,
解得x=2,
∴经过2秒PQ∥y轴;
②当点P在y轴右侧时,
依题意,得(6−2x)+x2×4=10,
解得x=1,
此时点P 的坐标为(4,4),
当点P在y轴左侧时,
依题意,得(2x−6)+x2×4=10,
解得x=113,
此时点P 的坐标为(−43,4).
综合以上可得点P的坐标为(4,4)或(−43,4).
9.【解答】解:(1)∵a+4+|2﹣b|=0,a+4≥0,|2﹣b|≥0,
∴a+4=0.,|2﹣b|=0,
∴a=﹣4,b=2,
∴c=12(a﹣b)=﹣3,
∴A(﹣4,0),B(0,2),C(﹣3,0),
∴BC=5,OA=4,
∴S△ABC=12×BC×OA=12×5×4=10;
(2)由题意知:OQ'=2×3=6,AA'=3m,
∵S△A'Q'A=S△CQ'O+S梯形AA'CO,
∴12×10×3m=12×6×3+12×(3+3m)×4,
∴m=53.
(3)连接OD,OE,
设D(m,n),
∵S△AOB=S△AOD+S△DOB,
∴12×4×2=12×4×n+12×2×(﹣m),
∴m=2n﹣4,
∵点D向右平移4个单位长度得到E点,
∴E(2n,n),
∵S△AOC+S△AOE+S△COE=S△ACE,
∴12×4×3+12×4×n+12×3×2n=14,
∴n=85,
∴m=2n﹣4=−45,
∴D(−45,85).
10.【解答】解:(1)由平移得,C(0+4,3),即C(4,3),
故答案为:(4,3);
(2)①由(1)知,C(4,3),
∵CD⊥x轴,
∴D(4,0),CD=3,
∵E(1,0),
∴DE=4﹣1=3,
∵CD⊥x轴,EF⊥x轴,
∴CD∥EF,
∵点P在射线FE上,
∴S△PCD=12CD•DE=12×3×3=4.5,
即△PCD的面积是定值,其定值为4.5;
②由(1)知,C(4,3),
∵A(﹣4,0),
设直线AC的解析式为y=kx+b,
∴−4k+b=04k+b=3,
∴k=38b=32,
∴直线AC的解析式为y=38x+32,
设点P(1,m)(m≤3),
记EF与AC的交点为Q,则Q(1,158),
当点P和点F重合时,P(1,3),
∴PQ=3−158=98,
此时,S△PAC=12PQ•(xC﹣xA)=12×98×(4+4)=9<332,
∴点P只能在AC下方,则PQ=158−m,
∴S△PAC=12PQ•(xC﹣xA)=12×(158−m)×(4+4)=332,
∴m=−94,
∴P(1,−94),∴t=(3+94)÷1=214,即t的值为214
中考数学压轴题3: 这是一份中考数学压轴题3,共8页。
2021学年10.4 列方程组解应用题教案及反思: 这是一份2021学年10.4 列方程组解应用题教案及反思,共5页。教案主要包含了教学目标,重点,教学过程等内容,欢迎下载使用。
第12讲 圆综合压轴题-2021年中考数学二轮复习重点题型针对训练(北师大版): 这是一份第12讲 圆综合压轴题-2021年中考数学二轮复习重点题型针对训练(北师大版),共23页。教案主要包含了方法梳理,强化巩固练习,答案详解等内容,欢迎下载使用。