
所属成套资源:2023年九年级数学中考专题训练
2023年九年级数学中考专题训练:二次函数综合压轴题(面积问题)及答案
展开
这是一份2023年九年级数学中考专题训练:二次函数综合压轴题(面积问题)及答案,共13页。试卷主要包含了综合与探究等内容,欢迎下载使用。
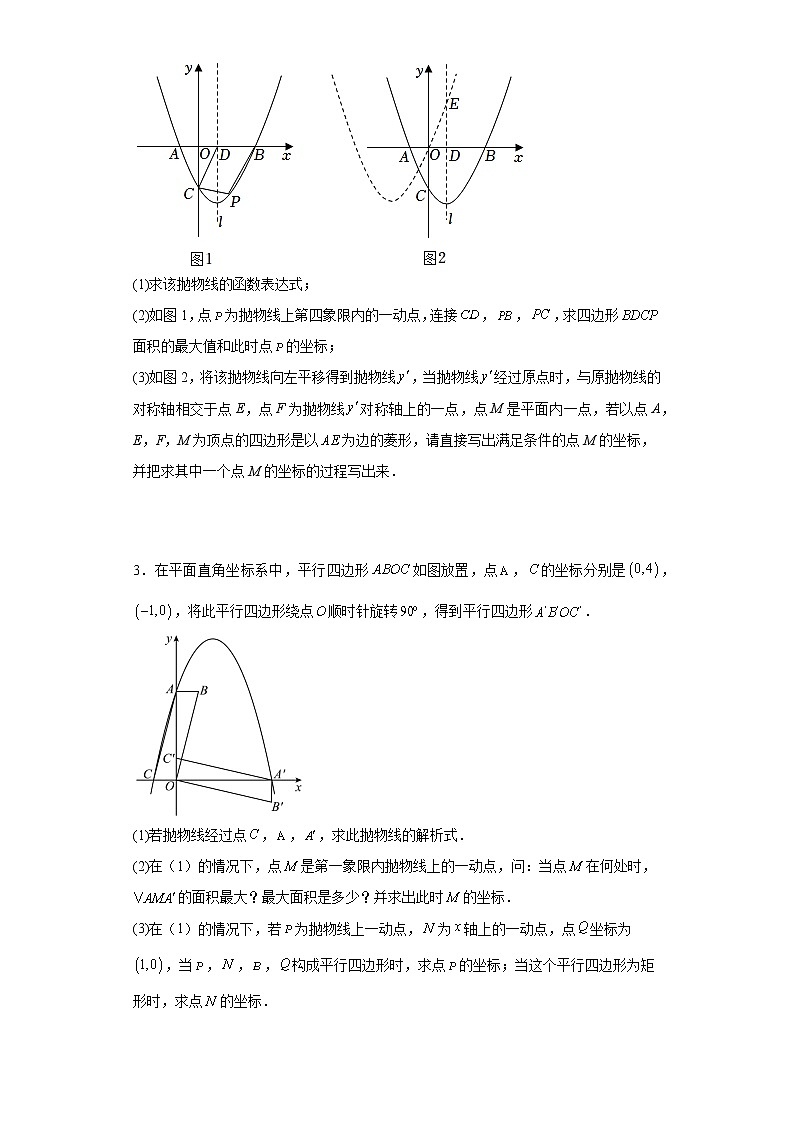
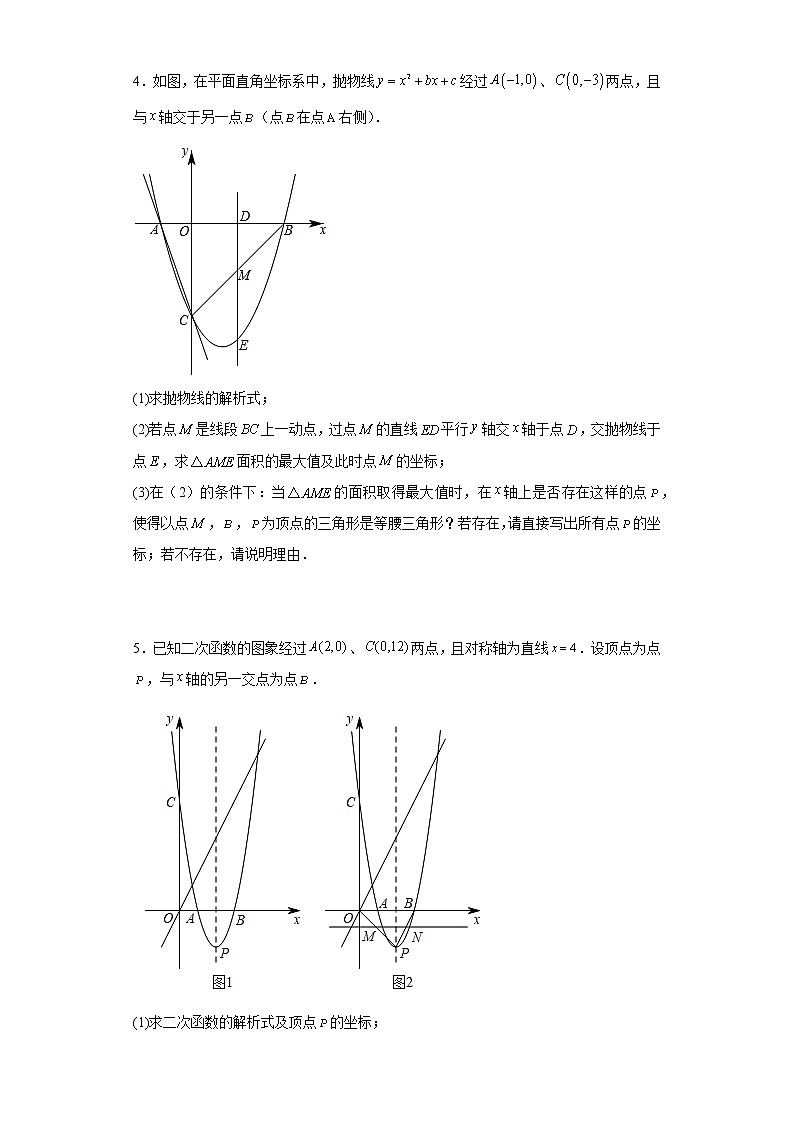
2023年九年级数学中考专题训练:二次函数综合压轴题(面积问题) 1.如图,、是平面直角坐标系中两点,其中m为常数,且,为轴上一动点,以为边在轴上方作矩形,使, 画射线, 把绕点C逆时针旋转得,连接,抛物线()过E两点.(1)填空: ____________, 用 表示点的坐标:___________.(2)当抛物线的顶点为,抛物线与线段交于点P,且与矩形的面积相等时,求m与n的关系式;(3)若E与原点重合,抛物线与射线的另一个交点为M,过M作垂直轴,垂足为N:①求满足的关系式;②当m为定值,抛物线与四边形有公共点,线段的最大值为5,请你直接写出a的取值范围. 2.如图,在平面直角坐标系中,抛物线与x轴交于,两点,其对称轴直线与x轴交于点 D.(1)求该抛物线的函数表达式;(2)如图1,点为抛物线上第四象限内的一动点,连接,,,求四边形面积的最大值和此时点的坐标;(3)如图2,将该抛物线向左平移得到抛物线,当抛物线经过原点时,与原抛物线的对称轴相交于点E,点F为抛物线对称轴上的一点,点M是平面内一点,若以点A,E,F,M为顶点的四边形是以为边的菱形,请直接写出满足条件的点M的坐标,并把求其中一个点M的坐标的过程写出来. 3.在平面直角坐标系中,平行四边形如图放置,点,的坐标分别是,,将此平行四边形绕点顺时针旋转,得到平行四边形.(1)若抛物线经过点,,,求此抛物线的解析式.(2)在(1)的情况下,点是第一象限内抛物线上的一动点,问:当点在何处时,的面积最大?最大面积是多少?并求出此时的坐标.(3)在(1)的情况下,若为抛物线上一动点,为轴上的一动点,点坐标为,当,,,构成平行四边形时,求点的坐标;当这个平行四边形为矩形时,求点的坐标. 4.如图,在平面直角坐标系中,抛物线经过、两点,且与轴交于另一点(点在点右侧).(1)求抛物线的解析式;(2)若点是线段上一动点,过点的直线平行轴交轴于点,交抛物线于点,求面积的最大值及此时点的坐标;(3)在(2)的条件下:当的面积取得最大值时,在轴上是否存在这样的点,使得以点,,为顶点的三角形是等腰三角形?若存在,请直接写出所有点的坐标;若不存在,请说明理由. 5.已知二次函数的图象经过、两点,且对称轴为直线.设顶点为点,与轴的另一交点为点.(1)求二次函数的解析式及顶点的坐标;(2)如图1,在直线上是否存在点,使?若存在,求出点的坐标;若不存在,请说明理由;(3)如图2,点是线段上的一个动点(O、P两点除外),以每秒个单位长度的速度由点向点运动,过点作直线轴,交于点.将沿直线对折,得到.在动点的运动过程中,设与梯形的重叠部分的面积为,运动时间为秒.求关于的函数关系式. 6.如图,抛物线与轴交于,两点,与轴交于点,一次函数经过点,,点是抛物线上的动点,过点作轴,垂足为,交直线于点.(1)求抛物线的解析式及点的坐标;(2)当点位于直线上方且面积最大时,求线段的长;(3)是否存在点,使得以,,,为顶点的四边形是平行四边形?若存在,请求出点的坐标;若不存在,请说明理由. 7.如图1,直线交轴于点,交轴于点,过、两点的抛物线与轴的另一交点为.(1)请直接写出该抛物线的函数解析式;(2)点是第二象限抛物线上一点,设点横坐标为.①如图2,连接,,,求面积的最大值;②如图3,连接,将线段绕点顺时针旋转,得到线段,过点作轴交直线于.求线段的最大值及此时点的坐标. 8.如图,抛物线与轴相交于A、B两点(点A在点B的左侧),与轴相交于点,顶点为(1)直接写出、、三点的坐标和抛物线的对称轴;(2)连接,与抛物线的对称轴交于点,点为线段上的一个动点,过点作交抛物线于点,设点的横坐标为;①用含的代数式表示线段的长,并求出当为何值时,四边形为平行四边形?②设的面积为S,求S与的函数关系式 9.综合与探究如图,已知抛物线与轴交于,两点(点在点的左侧),与轴交于点.(1)求抛物线的解析式;(2)在抛物线的对称轴上存在一点,使得的值最小,此时点的坐标为______;(3)点是第一象限内抛物线上的一个动点(不与点,重合),过点作轴于点,交直线于点,连接,直线把的面积分成两部分,使,请求出点的坐标;(4)若为抛物线的对称轴上的一个动点,是否存在点,使得是以为直角边的直角三角形,若存在,请直接写出点的坐标;若不存在,请说明理由. 10.如图,已知抛物线与x轴交于,两点(点A在点B的左侧),与y轴交于点C.(1)求抛物线的解析式;(2)点D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作轴于点F,交直线于点E,连接,直线能否把分成面积之比为的两部分?若能,请求出点D的坐标;若不能,请说明理由.(3)连接交于点Q,当的值为最小时,直接写出此时点D的坐标. 11.如图,已知二次函数的顶点是,且图象过点,与轴交于点.(1)求二次函数的解析式;(2)求直线的解析式;(3)在直线上方的抛物线上是否存在一点,使得,如果存在,请求出C点的坐标,如果不存在,请说明理由. 12.如图,抛物线与x轴交于点A和B,与y轴交于点C.(1)求A、B、C三点坐标;(2)如图1,动点P从点A出发,在线段上以每秒1个单位长度向点B做匀速运动,同时,动点Q从点B出发,在线段上以每秒个单位长度向点C做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接,设运动时间为t秒,问P、Q两点运动多久后的面积S最大,最大面积是多少?(3)如图2,点D为抛物线上一动点,直线交y轴于点E,直线交y轴于点F,求的值. 13.如图,抛物线.与x轴交于A,B两点,与y轴交于,直线经过点A且与抛物线交于另一点D.(1)求抛物线的解析式;(2)若P是位于直线上方的抛物线上的一个动点,连接,,求的面积的最大值;(3)在第(2)问的条件下,求点P到直线的最大值. 14.如图,抛物线与x轴交于,两点,与y轴交于点C.(1)求该抛物线的解析式;(2)在抛物线的对称轴1上是否存在一点M,使MA+MC的值最小?若存在,求出点M的坐标,若不存在,请说明理由;(3)若点D是抛物线上的一点,且位于直线BC上方,连接CD、BD、AC,当四边形ABDC的面积有最大值时,求点D的坐标及四边形ABDC的面积. 15.已知:如图,抛物线与坐标轴分别交于点,,,点P是线段上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P运动到什么位置时,的面积有最大值,面积最大值是多少?(3)已知抛物线的顶点为点D.点M是x轴上的一个动点,当点M的坐标为多少时,的周长最小?最小值是多少? 16.如图,经过原点的抛物线与轴交于另一点,在第一象限内与直线交于. (1)求点的坐标.(2)求这条抛物线的表达式.(3)在第四象限内的抛物线上有一点,满足以为顶点的三角形的面积为,求点的坐标(写出解题过程). 17.如图,关于x的二次函数的图象与x轴交于A、B两点,与y轴交于点C,且过点.(1)求b的值及该二次函数图象的对称轴;(2)连接,求的面积;(3)在上方抛物线上有一动点M,请直接写出的面积取到最大值时,点M的坐标.18.如图在平面直角坐标系中,抛物线分别交x轴于A、B两点、交y轴于点C、交直线OD于点D,直线OD的解析式为,D点的横坐标是4.(1)如图1,求抛物线的解析式;(2)如图2,点P在第二象限的抛物线上,连接PC、PD、CD,设P点的横坐标是t,△PCD的面积是S,求S与t的函数解析式(不要求写自变量取值范围);(3)如图3,在(2)的条件下,点E在y轴正半轴,点F在射线OD上,若,,,求点P的坐标.
参考答案:1.(1),(2)(3)①;② 2.(1)(2)的最大值为17,此时点P的坐标为(3)点M的坐标为或或或, 3.(1)(2)当的坐标为时,的面积最大,最大面积为(3)的坐标为或或或;的坐标为或5.(1),顶点P坐标为;(2)存在点D使,此时或;(3)当时,;当时, 6.(1),;(2)2;(3)存在,或或. 7.(1)(2)①4② 8.(1),,对称轴是x=1(2)①,当时,四边形为平行四边形;② 9.(1)(2)(3)(4)或 10.(1)(2)能,点D的坐标为或(3)M点的坐标为 11.(1);(2);(3)存在,或. 12.(1)、,(2)运动秒时,有最大值,最大值为(3) 13.(1);(2);(3). 14.(1);(2)存在,,;(3);9. 15.(1)(2)(3),周长最小值为 16.(1)(2,2)(2)(3)(1,-1) 17.(1),二次函数对称轴为直线(2)3(3) 18.(1)(2)(3)
相关试卷
这是一份北师大中考数学二次函数压轴题题分类专题(面积角度问题)(无答案),共41页。
这是一份专题03 二次函数中面积问题压轴真题训练-挑战2023年中考数学压轴真题汇编(全国通用),文件包含专题03二次函数中面积问题压轴真题训练解析版docx、专题03二次函数中面积问题压轴真题训练原卷版docx等2份试卷配套教学资源,其中试卷共78页, 欢迎下载使用。
这是一份中考数学压轴题满分突破训练 专题07 二次函数-面积最大值问题,文件包含专题07二次函数-面积最大值问题解析版docx、专题07二次函数-面积最大值问题原卷版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。









