2023年九年级数学中考专题训练：二次函数综合压轴题（角度问题）及答案

2023年九年级数学中考专题训练：二次函数综合压轴题（角度问题）

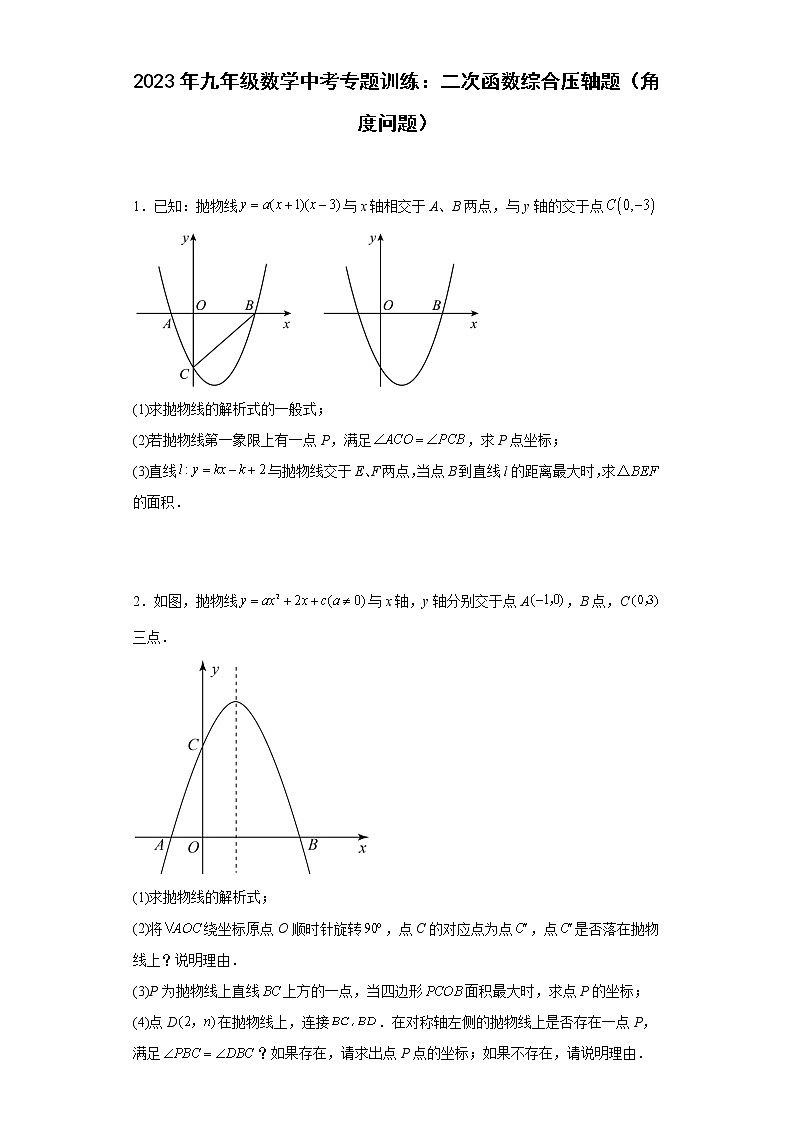
1．已知：抛物线与x轴相交于A、B两点，与y轴的交于点

(1)求抛物线的解析式的一般式；

(2)若抛物线第一象限上有一点P，满足，求P点坐标；

(3)直线与抛物线交于E、F两点，当点B到直线l的距离最大时，求的面积．

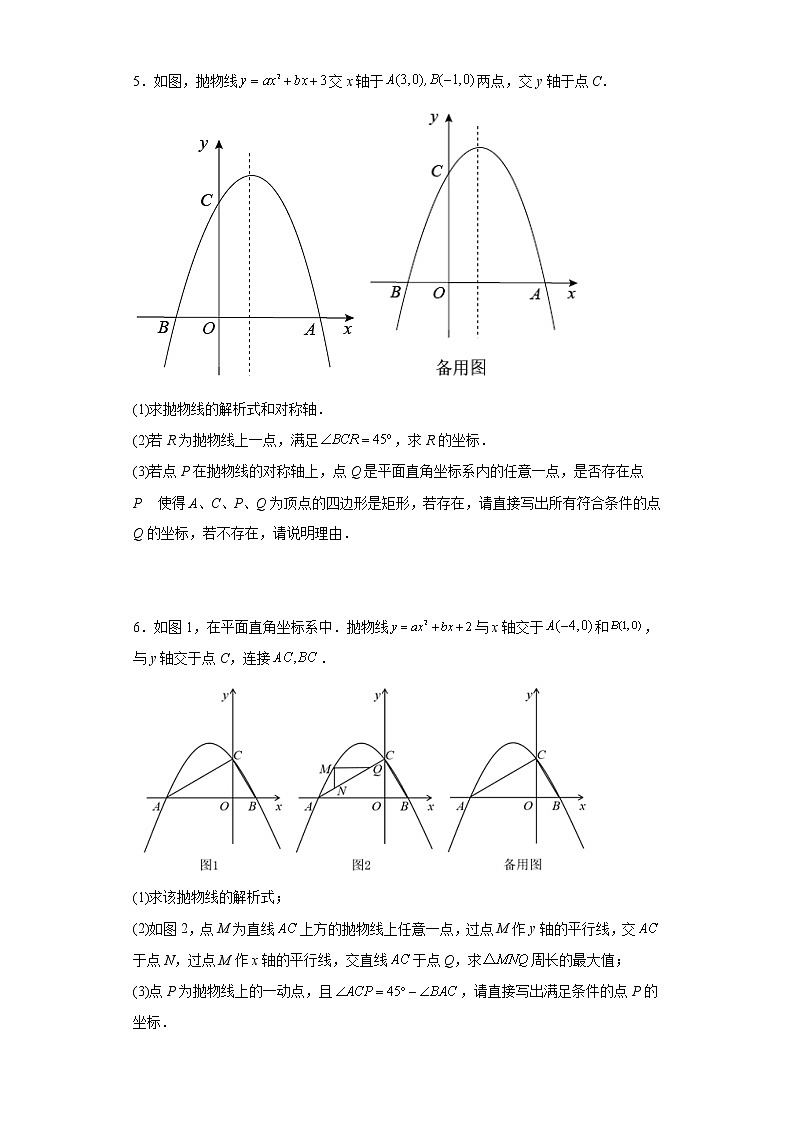
2．如图，抛物线与x轴，y轴分别交于点A，B点，C三点．

(1)求抛物线的解析式；

(2)将绕坐标原点O顺时针旋转，点C的对应点为点，点是否落在抛物线上？说明理由．

(3)P为抛物线上直线上方的一点，当四边形面积最大时，求点P的坐标；

(4)点D在抛物线上，连接．在对称轴左侧的抛物线上是否存在一点P，满足？如果存在，请求出点P点的坐标；如果不存在，请说明理由．

3．已知点C为抛物线的顶点．

(1)直接写出点C的坐标为                  ；

(2)若抛物线经过点．

①直接写出抛物线解析式为：                  ；

②如图1，点B，以为底的等腰交抛物线于点P，将点P绕原点O顺时针旋转到，求的坐标；

(3)如图2，过抛物线上一点M作直线l平行于y轴，直线交抛物线另一点于E，交直线l于点D，过M作轴，交抛物线于另一点N，过E作于点F．若点M的横坐标为，试探究与之间的数量关系并说明理由．

4．如图，在平面直角坐标系xOy中，抛物线与x轴相交于原点O和点，点在抛物线上．

(1)求抛物线的表达式，并写出它的对称轴；

(2)求的值；

(3)点D在抛物线上，如果，求点D的坐标．

5．如图，抛物线交x轴于两点，交y轴于点C．

(1)求抛物线的解析式和对称轴．

(2)若R为抛物线上一点，满足，求R的坐标．

(3)若点P在抛物线的对称轴上，点Q是平面直角坐标系内的任意一点，是否存在点P    使得A、C、P、Q为顶点的四边形是矩形，若存在，请直接写出所有符合条件的点Q的坐标，若不存在，请说明理由．

6．如图1，在平面直角坐标系中．抛物线与x轴交于和，与y轴交于点C，连接．

(1)求该抛物线的解析式；

(2)如图2，点M为直线上方的抛物线上任意一点，过点M作y轴的平行线，交于点N，过点M作x轴的平行线，交直线于点Q，求周长的最大值；

(3)点P为抛物线上的一动点，且，请直接写出满足条件的点P的坐标．

7．在平面直角坐标系xOy中，已知抛物线交x轴于，两点，与y轴交于点．

(1)求抛物线的函数解析式；

(2)如图1，点D为直线BC上方抛物线上一动点，连接AD，交BC于点E，求的最大值；

(3)如图2，点P为抛物线上一动点，是否存在点P，使得2∠PCB＝∠OCB，若存在，请直接写出点P的坐标；若不存在，请说明理由．

8．如图，在平面直角坐标系中，抛物线与x轴交于A、B两点（点B在点A的右侧），与y轴交于点C，D为线段AB上一点．

(1)求A，B，C三点的坐标；

(2)过点D作x轴的垂线与抛物线交于点E，与直线BC相交于点F，求出点E到直线BC距离d的最大值；

(3)连接CD，作点B关于CD的对称点，连接，．在点D的运动过程中，能否等于45°？若能，请直接写出此时点的坐标，若不存在请说明理由．

9．图，抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，连接AC、BC．点P沿AC以每秒1个单位长度的速度由点A向点C运动，同时，点Q沿BO以每秒2个单位长度的速度由点B向点O运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ．过点Q作QD⊥x轴，与抛物线交于点D，与BC交于点E，连接PD，与BC交于点F．设点P的运动时间为t秒（t＞0）．

(1)求直线BC的函数表达式；

(2)求出P，D两点的坐标（用含t的代数式表示，结果需化简）；

(3)试探究在点P，Q运动的过程中，是否存在某一时刻，使得点F为PD的中点？若存在，请直接写出此时t的值与F的坐标；若不存在，请说明理由．

10．如图，抛物线与轴交于，两点，与轴交于点，点是抛物线的顶点．

(1)求抛物线的解析式．

(2)点是轴负半轴上的一点，且，点在对称轴右侧的抛物线上运动，连接，与抛物线的对称轴交于点，连接，当平分时，求点的坐标．

(3)直线交对称轴于点，是坐标平面内一点，请直接写出与全等时点的坐标．

11．抛物线y＝ax2+c（a<0）与x轴交于A、B两点，顶点为C，点P在抛物线上，且位于x轴上方．

(1)如图1，若P(1，2)，A(-3，0)．

①求该抛物线的解析式；

②若D是抛物线上异于点P一点，满足∠DPO＝∠POB，求点D的坐标；

(2)如图2，已知直线PA、PB与y轴分别交于E、F两点．当点P运动时，是否为定值？若是，试求出该定值；若不是，请说明理由．

12．在平面直角坐标系中，抛物线交x轴于A、B两点（点A在点B的左），交y轴于点C

(1)当时，

①如图1，求△ABC的面积；

②如图2，若抛物线上有一点P，且，求点P的坐标

(2)过点B且与抛物线仅有一个交点的直线交y轴于点D，求的值．

13．如图1，一次函数y＝x﹣4的图象分别与x轴，y轴交于B，C两点，二次函数y＝ax2﹣x＋c的图象过B，C两点，且与x轴交于另一点A．

(1)求二次函数的表达式；

(2)点P是二次函数图象的一个动点，设点P的横坐标为m，若∠ABC＝2∠ABP．求m的值；

(3)如图2，过点C作CD∥x轴交抛物线于点D．点M是直线BC上一动点，在坐标平面内是否存在点N，使得以点C，D，M，N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

14．如图，已知直线y＝2x+n与抛物线y＝ax2+bx+c相交于A，B两点，抛物线的顶点是A（1，﹣4），点B在x轴上．

(1)求抛物线的解析式；

(2)若点M是y轴上一点，点N是坐标平面内一点，当以A、B、M、N为顶点的四边形是矩形时，求点M的坐标．

(3)在抛物线上是否存在点Q，使∠BAQ＝45°，若存在，请直接写出点Q的横坐标；若不存在，说明理由．

15．如图，抛物线y＝﹣x2+（m﹣1）x+m（其中m＞1）与x轴交于A，B两点，与y轴交于点C，点D在该抛物线的对称轴上，且DA＝DC．

(1)点A的坐标为 　　，用含m的式子表示点D的坐标为 　　；

(2)若△ACD与△BCO的面积之比为5：9，求该抛物线的表达式；

(3)在（2）的条件下，若动点P在该抛物线上，且当∠PBC＝∠DAB时，求点P的坐标．

16．如图，抛物线y＝x2+bx+c交x轴于点A，B两点，OA＝1，与y轴交于点C，连接AC，tan∠OAC＝3，抛物线的对称轴与x轴交于点D．

(1)求点A，C的坐标；

(2)若点P在抛物线上，且满足∠PAB＝2∠ACO，求直线PA与y轴交点的坐标；

(3)点Q在抛物线上，且在x轴下方，直线AQ，BQ分别交抛物线的对称轴于点M、N．求证：DM+DN为定值，并求出这个定值．

17．如图，抛物线与轴，轴分别交于点，点，三点．

（1）求抛物线的解析式；

（2）将绕坐标原点顺时针旋转90°，点的对应点为点，点是否落在抛物线上？说明理由．

（3）为抛物线上直线BC上方的一点，当四边形PCOB面积最大时，求点的坐标；

（4）点在抛物线上，连接BC，BD．在对称轴左侧的抛物线上是否存在一点，满足？如果存在，请求出点点的坐标；如果不存在，请说明理由．

18．如图，直线y＝﹣x＋3与x轴、y轴分别交于B、C两点，抛物线y＝﹣x2＋bx＋c经过B、C两点，与x轴另一交点为A，顶点为D．

（1）求抛物线的解析式．

（2）如果一个圆经过点O、点B、点C三点，并交于抛物线AC段于点E，求∠OEB的度数．

（3）在抛物线的对称轴上是否存在点P，使△PCD为等腰三角形，如果存在，直接写出点P的坐标，如果不存在，请说明理由．

（4）在抛物线的对称轴上是否存在一点P，使∠APB＝∠OCB？若存在，求出PB2的值；若不存在，请说明理由．

参考答案：

1．(1)

(2)或

(3)10

2．(1)

(2)点落在抛物线上

(3)点P的坐标为

(4)存在，P坐标为

3．(1)

(2)①；②的坐标为；

(3)

4．(1)，直线

(2)3

(3)或

5．(1)，对称轴为直线

(2)（4，-5）

(3)存在，（4，1）或（-2，1）或或

6．(1)

(2)

(3)或

7．(1)

(2)的最大值为

(3)存在，或

8．(1)A（-2，0），B（3，0），C（0，3）；

(2)点E到直线BC的距离d的最大值为；

(3)在点D的运动过程中，∠ADB'能等于45°，此时点B′的坐标为（0，-3）或（-3，3）．

9．(1)

(2)，

(3)存在，t=3，，

10．(1)或

(2)

(3)或或或．

11．(1)①；②(-1，2)或(，)

(2)是定值，定值为2．

12．(1)①3；②

(2)1

13．(1)

(2)或

(3)存在，N1（1，﹣5），N2（﹣1，﹣3），N3（3，﹣3）

14．(1)

(2)点M坐标为：（0，）或（0，）或（0，﹣1）或（0，﹣3）

(3)存在，点Q的横坐标为﹣2或

15．(1)（﹣1，0），

(2)y＝﹣x2+2x+3

(3)点P的坐标为（2，3）和

16．(1)点A、C的坐标分别为（1，0）、（0，﹣3）

(2)直线PA在与y轴交点的坐标为（0，）或（0，）

(3)证明见解析，DM+DN＝8

17．（1）；（2）点落在抛物线上；（3）P(,)；（4）(，)．

18．（1）y＝﹣x2+2x+3；（2）45°；（3）存在，点P（1，2）、（1，3）、（1，4）、（1，4+）、（1，4﹣）；（4）存在，16+8．