【期末考前必练】2022-2023学年苏科版数学八年级上册期末考点必刷题：专练01 选择题-基础（30题）

这是一份【期末考前必练】2022-2023学年苏科版数学八年级上册期末考点必刷题：专练01 选择题-基础（30题），文件包含期末考前必练2022-2023学年苏科版数学八年级上册期末考点必刷题专练01选择题-基础30题解析版docx、期末考前必练2022-2023学年苏科版数学八年级上册期末考点必刷题专练01选择题-基础30题原卷版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。

专练01 选择题-基础（30题）
1．（2021·云南盘龙·八年级期末）如图，，再添加一个条件，不能判定的是（ ）

A． B． C． D．
【答案】B
解：由题意得：∠CAB=∠DBA，AB=BA，
当AC=BD时，可以利用SAS证明△ABC≌△BAD，故A选项不符合题意；
当AD=BC时，可以利用SSA不能证明△ABC≌△BAD，故B选项符合题意；
当∠DAB=∠CBA时，可以利用ASA证明△ABC≌△BAD，故C选项不符合题意；
当∠C=∠D时，可以利用AAS证明△ABC≌△BAD，故D选项不符合题意；
故选B．
【点睛】
本题主要考查了全等三角形的判定，解题的关键在于能够熟练掌握全等三角形的判定条件．
2．（2021·黑龙江·大庆市庆新中学八年级期末）某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是（ ）．

A．带①去 B．带②去 C．带③去 D．①②③都带
【答案】C
带③去，理由如下：
∵③中满足ASA的条件，
∴带③去，
故选C．
【点睛】
本题考查了三角形全等的判定，熟练掌握三角形全等的判定定理是解题的关键．
3．（2021·河南汝州·八年级期末）如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB＝8，DO＝3，平移距离为4，则阴影部分的面积为（　　）

A．18 B．24 C．26 D．32
【答案】C
解：由题意得： ，
∴DE=AB=8，，
∵平移距离为4，
∴BE=4，
∵AB＝8，DO＝3，
∴OE=AB-DO=5，
∴阴影部分的面积等于
．
故选：C．
【点睛】
本题主要考查了图形的变换——平移，熟练掌握平移前后图形的大小形状完全相同是解题的关键．
4．（2021·广西崇左·八年级期末）下列条件中，不能判定两个直角三角形全等的是（ ）
A．一个锐角和斜边对应相等 B．两条直角边对应相等
C．两个锐角对应相等 D．斜边和一条直角边对应相等
【答案】C
解：A、若一个锐角和斜边分别对应相等，可用AAS证这两个直角三角形全等，故选项说法正确，不符合题意；
B、若两条直角边对应相等，可用SAS证这两个直角三角形全等，故选项说法正确，不符合题意；
C、若两个锐角对应相等，不能证这两个直角三角形全等，故选项说法错误，符合题意；
D、若斜边和一条直角边对应相等，可用HL证这两个直角三角形全等，故选项说法正确，不符合题意；
故选：C．
【点睛】
本题考查了直角三角形的全等判定，熟练运用直角三角形的全等判定是本题的关键．
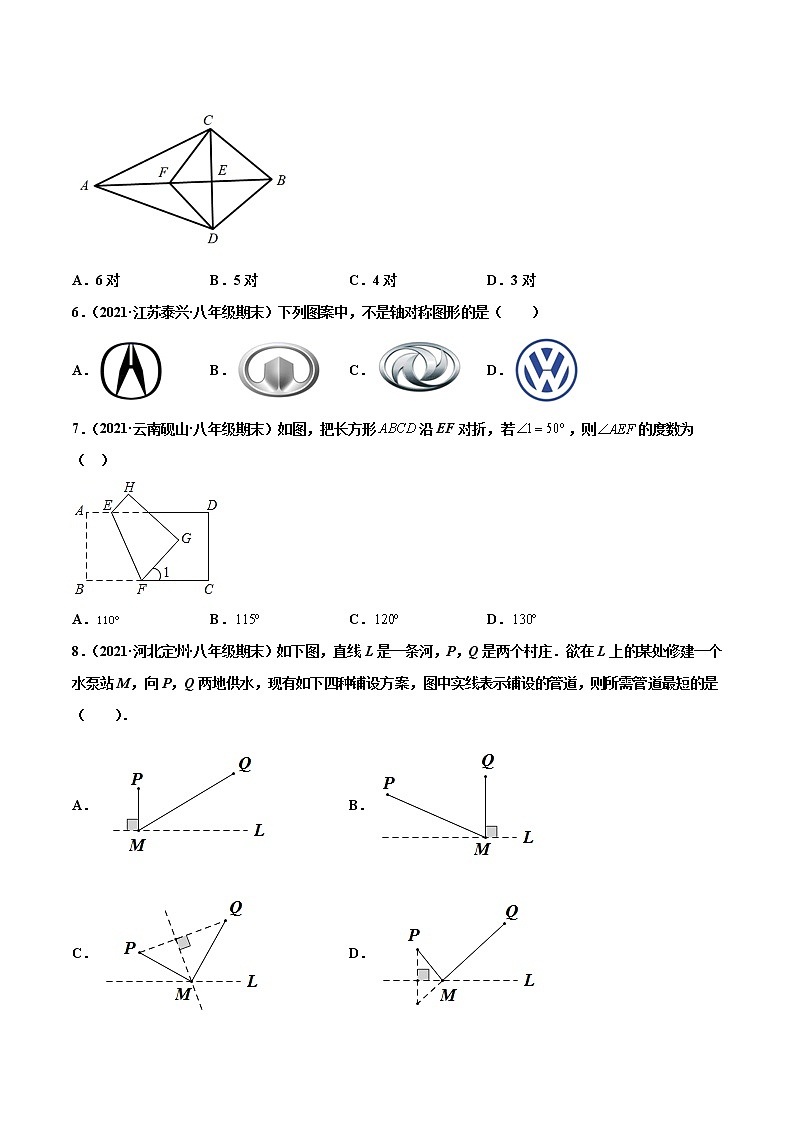
5．（2021·广东·东莞市光明中学八年级期末）如图，AC＝AD，BC＝BD，连结CD交AB于点E，F是AB上一点，连结FC，FD，则图中的全等三角形共有（　　）

A．6对 B．5对 C．4对 D．3对
【答案】A
解：在△ACB和ADB中，
，
∴△ACB≌ADB，
∴∠CAB=∠DAB，∠CBA=∠DBA，
∵AC＝AD，∠CAB=∠DAB，AF=AF
∴△CAF≌△DAF，CF=DF，
∵AC＝AD，∠CAB=∠DAB，AE=AE
∴△ACE≌△ADE，CE=DE，
∵BC＝BD，∠CBA=∠DBA，BE=BE
∴△CBE≌△DBE，
∵BC＝BD，∠CBA=∠DBA，BF=BF
∴△FCB≌△FDB，
∵CF=DF，CE=DE，EF=EF，
∴△CEF≌△DEF，
∴图中全等的三角形有6对，
故选：A．
【点睛】
本题考查了对全等三角形的判定定理的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．
6．（2021·江苏泰兴·八年级期末）下列图案中，不是轴对称图形的是（　　）
A． B． C． D．
【答案】C
解：A、是轴对称图形，故本选项不合题意；
B、是轴对称图形，故本选项不合题意；
C、不是轴对称图形，故本选项符合题意；
D、是轴对称图形，故本选项不合题意．
故选：C．
【点睛】
本题考查了轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．
7．（2021·云南砚山·八年级期末）如图，把长方形沿EF对折，若，则的度数为（ ）

A． B． C． D．
【答案】B
解：根据折叠以及∠1＝50°，得
∠BFE＝∠BFG＝（180°﹣∠1）＝65°．
∵AD∥BC，
∴∠AEF＝180°﹣∠BFE＝115°．
故选：B．
【点睛】
本题考查的是平行线的性质及图形翻折变换的性质，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
8．（2021·河北定州·八年级期末）如下图，直线L是一条河，P，Q是两个村庄．欲在L上的某处修建一个水泵站M，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（ ）．
A． B．C． D．
【答案】D
解：如图，作点P关于直线l的对称点P'，连接QP'交直线l于M．

则
根据两点之间，线段最短，可知选项D修建的管道，则所需管道最短．
故选：D．
【点睛】
本题考查了最短路径的数学问题．这类问题的解答依据是“两点之间，线段最短”．由于所给的条件的不同，解决方法和策略上又有所差别．
9．（2021·浙江莲都·八年级期末）如图，在△ABC中，用圆规在BA，BC上分别截取BD，BE，使BD=BE，分别以D，E为圆心、大于DE的长为半径画弧，两弧在∠ABC内交于点F，连接BF并延长交AC于点G．若AB=3，BC=5，S△ABC=32，则△BCG的面积是（ ）

A．20 B． C． D．12
【答案】A
解：由作法得BG平分∠ABC，
作GM⊥AB于M，GN⊥BC于N，如图，

则GM＝GN，
∵S△GAB+S△GBC=S△ABC，
∴GM×3+GN×5=32，
即3GN＋5GN=64，解得GN=8，
∴S△GBC=×5×8=20．
故选：A．
【点睛】
本题考查作图-复杂作图，角平分线的性质，解题的关键是理解题意，灵活运用所学知识解决问题．
10．（2021·全国·八年级期末）如图，△ABC中，EF是AB的垂直平分线，与AB交于点D，BF＝6，CF＝2，则AC的长度为（　　）

A．6 B．7 C．8 D．9
【答案】C
解：∵EF是AB的垂直平分线，BF＝6，
∴AF=BF=6，
∵CF＝2，
∴AC=AF＋CF=8．
故选：C．

【点睛】
本题考查的是垂直平分线的性质，掌握垂直平分线的性质找到相等线段是解决此题的关键．
11．（2021·陕西·西北工业大学附属中学八年级期末）有长为5cm，13cm的两根木条，现想找一根木条和这两根木条首尾顺次相连组成直角三角形，则下列木条长度适合的是（ ）
A．10cm B．12cm C．18cm D．20cm
【答案】B
解：∵52+132=，132-52=122，
∴木条长度适合的是12cm，
故选：B．
【点睛】
本题考查了勾股定理的应用，熟练掌握勾股定理是解题的关键．
12．（2021·河北唐县·八年级期末）下列三条线段不能组成直角三角形的是（ ）
A．a=5，b=12，c=13 B．a=6，b=8，c=10
C． D．a：b：c=2：3：4
【答案】D
解：A．∵52+122=132，
∴以a、b、c为边能组成直角三角形，故本选项不符合题意；
B．∵62+82=102，
∴以a、b、c为边能组成直角三角形，故本选项不符合题意；
C．∵()2+()2=()2，
∴以a、b、c为边能组成直角三角形，故本选项不符合题意；
D．∵22+32≠42，
∴以a、b、c为边不能组成直角三角形，故本选项符合题意；
故选：D．
【点睛】
本题考查了勾股定理的逆定理，注意：如果一个三角形的两边a、b的平方和等于第三边c的平方，那么这个三角形是直角三角形．
13．（2021·湖南绥宁·八年级期末）下列说法错误的是（ ）
A．△ABC中，若有∠A＋∠B＝∠C，则△ABC是直角三角形
B．△ABC中，若有∠A∶∠B∶∠C＝1∶2∶3，则△ABC是直角三角形
C．△ABC的三边长分别为：a，b，c，且a2﹣b2＝c2，则△ABC是直角三角形
D．在一个直角三角形中，有两边的长度分别是3和5，则第三边的长度是4
【答案】D
解：A、△ABC中，若有∠A＋∠B＝∠C，则∠C＝90°，∴△ABC是直角三角形，说法正确；
B、△ABC中，若有∠A∶∠B∶∠C＝1∶2∶3，则∠C＝90°，∴△ABC是直角三角形，说法正确；
C、△ABC的三边长分别为：a，b，c，且a2﹣b2＝c2，则a2＝b2＋c2，∴△ABC是直角三角形，说法正确；
D、在一个直角三角形中，有两边的长度分别是3和5，则第三边的长度是4或，说法错误；
故选：D．
【点睛】
本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．
14．（2021·广东黄埔·八年级期末）一根竹子高一丈，折断后竹子顶端落在离竹子底端6尺处，折断处离地面的高度是多少？（这是我国古代《九章算术》中的“折竹抵地问题．其中的丈、尺是长度单位，一丈＝10尺）设折断处离地面的高度为x尺，则可列方程为（ ）
A．x2＋62＝（10﹣x）2 B．x2﹣62＝（10﹣x）2
C．x2＋6＝（10﹣x）2 D．x2﹣6＝（10﹣x）2
【答案】A
解：1丈=10尺，
设折断处离地面的高度为x尺，则斜边为（10-x）尺，
根据勾股定理得：x2+62=（10-x）2，
故选：A．
【点睛】
此题考查了勾股定理的应用，解题的关键是利用题目信息构造直角三角形，从而运用勾股定理解题．
15．（2021·云南昆明·八年级期末）如图，一根竹子高1丈，折断后竹子顶端落在离竹子底端3尺处，则折断处离地面的高度为多少尺?（ ）（这是我国古代数学著作《九章算术》中的一个问题，其中的丈、尺是长度单位，1丈=10尺）

A．4尺 B．4.5尺 C．4.55尺 D．5尺
【答案】C
解：1丈=10尺
设竹子折断处离地面x尺，则斜边为（10﹣x）尺，
根据勾股定理得：，
解得：，
答：折断处离地面的高度是4.55尺，
故选：C．
【点睛】
此题考查了勾股定理的应用，解题的关键是利用题目信息构造直角三角形，从而运用勾股定理解题．
16．（2021·山东冠县·八年级期末）的平方根是（ ）
A． B． C．9 D．
【答案】A
，
的平方根是，
故选A．
【点睛】
本题考查了算术平方根的定义，求一个数的平方根，能熟记算术平方根的定义的内容是解此题的关键．
17．（2021·山东茌平·八年级期末）下列说法中不正确的是（ ）
A．是5的平方根 B．是的立方根
C．4的平方根是16 D．(-2)2的算术平方根是2
【答案】C
解：A、是5的平方根，正确；
B、是的立方根，正确；
C、4的平方根是，故本选项错误；
D、，4的算术平方根是2，正确；
故选：C．
【点睛】
本题考查了平方根、算术平方根、立方根，解决本题的关键是熟记平方根、算术平方根、立方根的定义．
18．（2021·江苏泗阳·八年级期末）计算的结果在（ ）
A．4至5之间 B．5至6之间 C．6至7之间 D．7至8之间
【答案】D
∵
∴
∴
即的结果在7至8之间
故选：D．
【点睛】
本题考查了算术平方根的估算，关键是确定算术平方根在哪两个相邻自然数之间．
19．（2021·湖南岳阳·八年级期末）已知，则的值是（ ）
A．1 B．-1 C．2020 D．-2020
【答案】A
解：因为，
所以，，
解得，，
所以，
故选：A．
【点睛】
本题考查非负数的意义，解题的关键是掌握算术平方根和绝对值的非负性．
20．（2021·辽宁建昌·八年级期末）的绝对值是（ ）
A． B． C． D．
【答案】B
的绝对值是．
故选B
【点睛】
本题考查了绝对值的意义，无理数大小的估算，比较无理数大小是解题的关键．
21．（2021·河北沧县·八年级期末）如图，在轴，轴上分别截取，，使，再分别以点，为圆心，以大于长为半径画弧，两弧交于点．若点的坐标为，则的值为（ ）

A．3 B．4 C．5 D．6
【答案】A
解：∵OA=OB，分别以点A，B为圆心，以大于AB长为半径画弧，两弧交于点P，
∴点P在∠BOA的角平分线上，
∴点P到x轴和y轴的距离相等，
又∵点P的坐标为（a，2a-3），且在第一象限，
∴a=2a-3，
∴a=3．
故选：A．
【点睛】
本题考查了作图-基本作图，角平分线的作法及其性质在坐标与图形性质问题中的应用，明确题中的作图方法及角平分线的性质是解题的关键．
22．（2021·河北沧县·八年级期末）点不可能在（ ）
A．轴上 B．轴上 C．第三象限 D．第四象限
【答案】A
解：当 时，点B横坐标为正，纵坐标为负，在第四象限，选项D正确；
当时，点B横坐标为负，纵坐标为负，在第三象限，选项C正确；
当时，点B横坐标为0，纵坐标为负，在y轴的负半轴上，选项B正确．
故选：A
【点睛】
本题考查点在坐标平面内的位置，根据题意分类讨论是关键．
23．（2021·海南海口·八年级期末）在平面直角坐标系中，若点A在第三象限，则点B所在的象限是（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【答案】B
解：∵点A（-a，b）在第三象限内，
∴-a＜0，b＜0，
∴a＞0，
∴点B（b，a）所在的象限是第二象限．
故选B．
【点睛】
本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点，熟练掌握四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）是解题的关键．
24．（2021·湖南岳阳·八年级期末）在平面直角坐标系中，点所在的象限为（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【答案】B
解：∵a2≥0，
∴-1-a2≤-1；
∵b2≥0，
∴3+b2≥3，
∴点A（-1-a2，3+b2）所在的象限为第二象限．
故选：B．
【点睛】
本题主要考查了平面直角坐标系中各象限的点的坐标的符号特点，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
25．（2021·江西南昌·八年级期末）如图，为直角三角形，，，则点的坐标为（ ）

A． B． C． D．
【答案】C
解：在Rt△OAB中，OA＝5，AB＝4，
由勾股定理得：OB＝，
∴A（3，4），
故选：C．
【点睛】
本题主要考查了勾股定理和坐标系中，点的坐标的表示，求出OB的长是解题的关键．
26．（2021·陕西·西北工业大学附属中学八年级期末）一次函数y＝kx﹣5的图象经过点（k，﹣1），且y随x的增大而减小，则这个函数的表达式是（ ）
A．yx﹣5 B．yx﹣5 C．y＝﹣2x﹣5 D．y＝2x﹣5
【答案】C
解：∵一次函数y＝kx﹣5的图象经过点（k，﹣1）
∴
∴
又y随x的增大而减小，
∴
∴
∴这个一次函数关系式为y＝﹣2x﹣5
故选：C
【点睛】
本题考查了待定系数法求一次函数解析式及一次函数的性质，正确求出要满足的条件是解答本题的关键．
27．（2021·河北唐县·八年级期末）关于一次函数y= -3x+4图像和性质的描述错误的是（ ）
A．y 随x的增大而减小 B．直线与x轴交点的坐标是( 0， 4 )
C．当x>0时，y<4 D．直线经过第一、二、四象限
【答案】B
∵一次函数中，，
∴y随x的增大而减小，
故A选项正确；
又∵，
∴与y轴的交点在x轴的上方，
∴直线经过第一、二、四象限，
故D选项正确；
∵当时，，且y随x的增大而减小，
∴当时，，
故C正确；
在中令，
解得：，
∴直线与x轴的交点坐标为（，0），
故B选项错误；
故选：B．
【点睛】
本题主要考查一次函数的性质，掌握一次函数的增减性、与坐标轴的交点坐标是解题的关键，注意与不等式相结合．
28．（2021·内蒙古阿拉善盟·八年级期末）已知正比例函数y＝kx(k≠0)的函数值y随x的增大而减小，则一次函数y＝x＋k的图象大致是（ ）
A． B． C． D．
【答案】B
正比例函数y＝kx(k≠0)的函数值y随x的增大而减小，

y＝x＋k的图象经过一、三、四象限.
故选B
【点睛】
本题考查的是一次函数的图象与系数的关系，即一次函数y=kx+b (k≠0) 中，当时，图象经过一、三、四象限.
29．（2021·内蒙古阿拉善盟·八年级期末）对于函数y＝－2x＋2，下列结论：①当x＞1时，y＜0；②它的图象经过第一、二、三象限；③它的图象必经过点(－2，2)；④y的值随x的增大而增大．其中正确结论的个数是（ ）
A．1 B．2 C．3 D．4
【答案】A
当时，－2x＋2<0，，①正确；
它的图象经过第一、二、四象限，②错误；
它的图象不经过，③错误；
y的值随x的增大而减小，④错误，
故正确结论只有1项，
故选：A．
【点睛】
本题考查的是一次函数的性质，同时考查了一次函数的图象与系数的关系，属于基础题，熟练掌握一次函数的性质是解题关键．
30．（2021·河北顺平·八年级期末）下列图象中，表示y是x的函数的是（ ）
A． B．C． D．
【答案】A
解：A、对于x的每一个取值，y都有唯一确定的值与之对应，故A正确；
B、对于x的每一个取值，y可能有三个值与之对应，故B错误；
C、对于x的每一个取值，y可能有两个值与之对应，故C错误；
D、对于x的每一个取值，y可能有两个值与之对应，故D错误；
故选：A．
【点睛】
主要考查了函数的定义，在一个变化过程中有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．