【期末考前必练】2022-2023学年人教版数学八年级上册期末考点必刷题：专练09 全等三角形大题（15题）

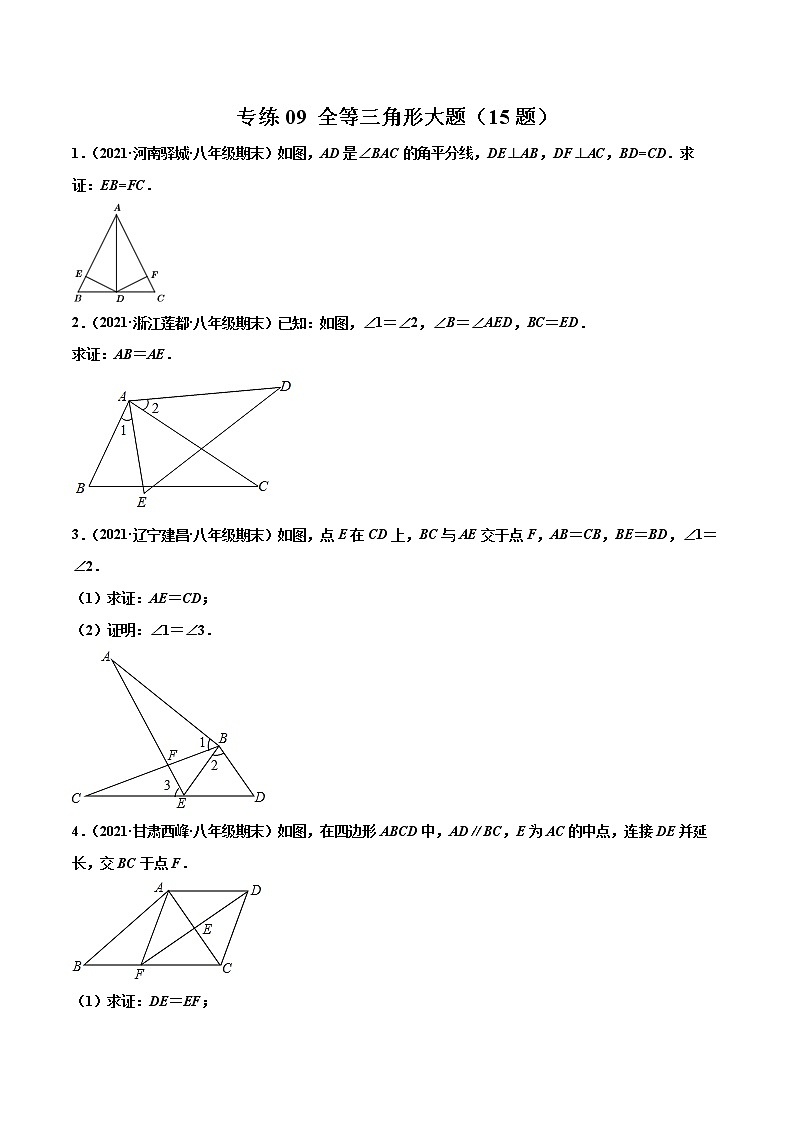
专练09 全等三角形大题（15题）

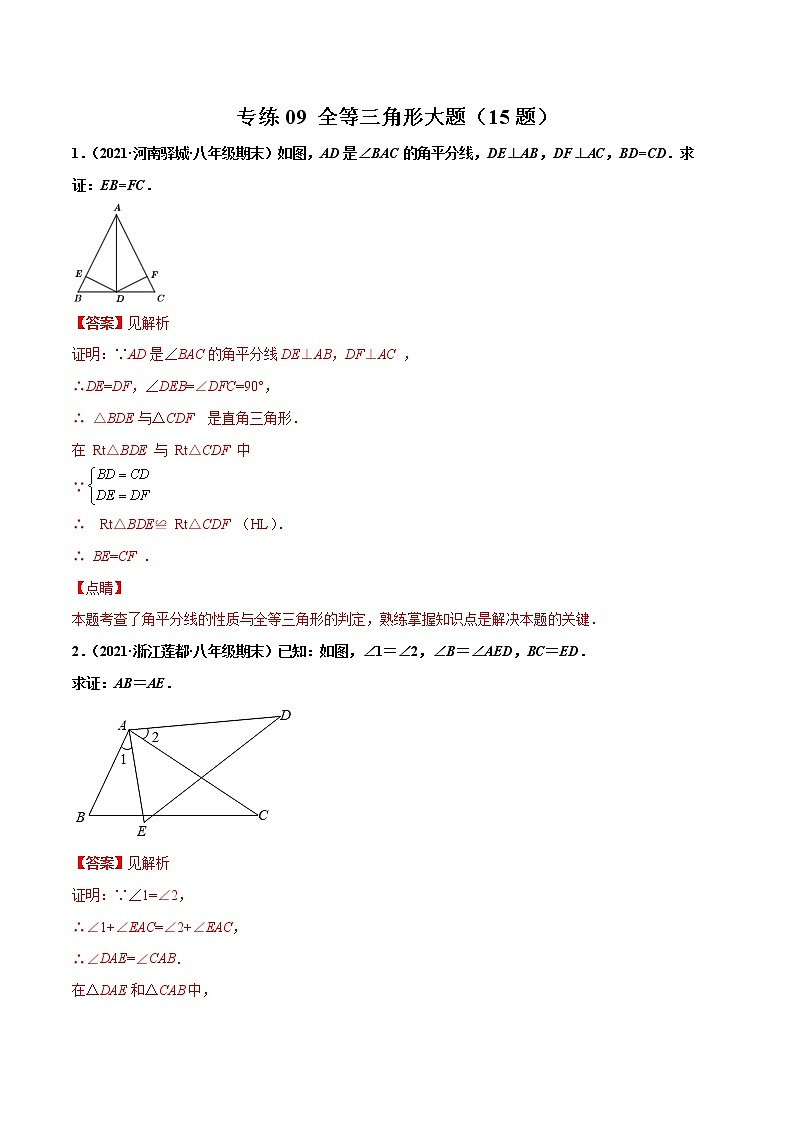
1．（2021·河南驿城·八年级期末）如图，AD是∠BAC的角平分线，DE⊥AB，DF⊥AC，BD=CD．求证：EB=FC．

【答案】见解析

证明：∵AD是∠BAC的角平分线DE⊥AB，DF⊥AC ， 

∴DE=DF，∠DEB=∠DFC=90°，

∴ △BDE与△CDF  是直角三角形．

在 Rt△BDE 与 Rt△CDF 中

∵

∴  Rt△BDE≌ Rt△CDF （HL）．

∴ BE=CF ．

【点睛】

本题考查了角平分线的性质与全等三角形的判定，熟练掌握知识点是解决本题的关键．

2．（2021·浙江莲都·八年级期末）已知：如图，∠1＝∠2，∠B＝∠AED，BC＝ED．

求证：AB＝AE．

【答案】见解析

证明：∵∠1=∠2，

∴∠1+∠EAC=∠2+∠EAC，

∴∠DAE=∠CAB．

在△DAE和△CAB中，

，

∴△DAE≌△CAB（AAS），

∴AB=AE．

【点睛】

本题考查了全等三角形的判定及性质，证明△DAE≌△CAB是解题的关键．

3．（2021·辽宁建昌·八年级期末）如图，点E在CD上，BC与AE交于点F，AB＝CB，BE＝BD，∠1＝∠2．

（1）求证：AE＝CD；

（2）证明：∠1＝∠3．

【答案】（1）见解析；（2）见解析

（1）证明：∵∠1=∠2，

∴∠ABE=∠CBD，

在△ABE和中，

∵，

∴△ABE≌△CBD（SAS），

∴AE＝CD；

（2）由（1）已证，知，△ABE≌△CBD

∴∠A=∠C，

又∵∠AFB=∠CFE，

∴∠1＝∠3．

【点睛】

本题考查了三角形全等的判定定理与性质、对顶角相等、三角形的内角和定理等知识点，熟练掌握三角形全等的判定定理与性质是解题关键．

4．（2021·甘肃西峰·八年级期末）如图，在四边形ABCD中，AD∥BC，E为AC的中点，连接DE并延长，交BC于点F．

（1）求证：DE＝EF；

（2）若AD＝12，BF：CF＝2：3，求BC的长．

【答案】（1）证明见解析；（2）BC=20．

（1）证明：∵AD∥BC，

∴∠DAE=∠FCE，∠ADE=∠EFC．

又∵E为AC的中点，

∴AE=CE．

在△ADE和△CFE中，

，

∴△ADE≌△CFE（AAS）．

∴DE=EF．

（2）解：∵△ADE≌△CFE，

∴AD=CF=12，

∵BF：CF=2：3，

∴BF=8，

∴BC=BF+CF=8+12=20．

【点睛】

此题考查了全等三角形的判定与性质，平行线的性质，熟练掌握全等三角形的判定与性质是解本题的关键．

5．（2021·吉林铁西·八年级期末）如图，，，，，垂足分别为，．

（1）求证：；

（2）若，，请直接写出的长．

【答案】（1）见解析；（2）5

解：（1）∵，，

∴，，

∴，

∵，，

∴，

∵，∴

（2）∵，

∴AD=CE，BE=CD，

∴．

【点睛】

本题考查了全等三角形的性质和判定，垂线的定义等知识点的应用，解答本题的关键是得出证明△ACD和△CBE全等的三个条件．

6．（2021·辽宁西丰·八年级期末）如图，点O是△ABC的边AC的中点，AF∥BC，DE⊥AC于点O，交AF于点D，交BC于点E，连接CD．

求证：CD＝CE．

【答案】见解析

证明：∵点O是△ABC的边AC的中点，

∴AO＝CO．

∵AD∥BC，

∴∠DAO＝∠ECO．

在△AOD和△COE中，

，

∴△AOD≌△COE（ASA），

∴DO＝EO．

在△COD和△COE中，

，

∴△COD≌△COE（SAS），

∴CD＝CE．

【点睛】

本题考查了全等三角形的判定与性质以及平行线的性质，利用全等三角形的判定定理，证出△AOD≌△COE及△COD≌△COE是解题的关键．

7．（2021·江西·南昌市心远中学八年级期末）如图，在和中，．

求的面积；

试判断的形状，并证明你结论．

【答案】（1）（2）直角三角形；理由见解析

解：（1）过点C作于E，

设，在和中，

，，

则，解得，

∴；

（2）为直角三角形，理由如下：

过点D作于F，

∵，

∴,

在三角形和中，

,

∴，

∴，，

∴,

则，

在中，

， ，

∴，

∴为直角三角形．

【点睛】

本题考查了勾股定理，解方程组，全等三角形的判定与性质，勾股定理逆定理等知识点，运用勾股定理求出需要的线段的长是解题的关键．

8．（2021·陕西商州·八年级期末）如图，、、三点在一条直线上，，，．求证：．

【答案】见详解

证明：∵，，，

又∵AB=AB，

∴（HL），

∴∠ABC=∠ABD，

又∵，BE=BE，

∴(SAS)，

∴．

【点睛】

本题主要考查全等三角形的判定和性质，熟练掌握SAS，HL证三角形全等是解题的关键．

9．（2021·广东·连南瑶族自治县教师发展中心八年级期末）已知：平分，点、都是上不同的点，，，垂足分别为、，连接、．求证：

（1）

（2）．

【答案】（1）证明见解析；（2）证明见解析．

（1）证明：∵平分

∴

∵，

∴

又∵

∴（AAS）

（2）证明：∵

∴

又∵平分

∴

又∵

∴（SAS）

∴

【点睛】

本题考查三角形全等的判定定理，角平分线的性质等相关知识点，根据定理切入解题是重点．

10．（2021·重庆彭水·八年级期末）如图，中， ，是上一点，满足，连接交于点，，交于点，连结．

（1）求证：．

（2）请你判断与的大小关系，并证明你的结论．

【答案】（1）见解析；（2），理由见解析

解：（1）∵，

∴

在和中，

∴

∴ 

（2） 

理由如下：

 ∵

∴

又∵

∴

在和中

∴

∴在中，即．

【点睛】

本题考查的是全等三角形的判定与性质、平行线的性质以及三角形边的性质，熟练掌握相关性质是解决本题的关键．

11．（2021·甘肃酒泉·八年级期末）如图所示，在△ABC中，D为BC的中点，DE⊥BC，交∠BAC的平分线AE于点E，EF⊥AB于点F，EG⊥AC交AC延长线于点G．求证：BF＝CG．

【答案】见解析．

证明：连接、，

，

为中点，

，

，，

且平分，

，

在和中，

，

，

．

【点评】

本题考查了全等三角形的判定：解题的关键是全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．

12．（2021·辽宁大连·八年级期末）如图，点B、E、C、F在一条直线上，，，．求证：．

【答案】见解析

证明：∵，

∴，

∵，

∴，即．

在和中

∴

∴．

【点睛】

本题主要考查了平行线的性质，全等三角形的性质与判定，解题的关键在于能够熟练掌握相关知识进行求解.

13．（2021·辽宁兴城·八年级期末）如图，，且，，是上两点，，．

求证：．

【答案】见详解

证明∵AB⊥CD，CE⊥AD，BF⊥AD，

∴∠C＋∠D＝90°，∠A＋∠D＝90°，∠AFB＝∠CED＝90°

∴∠A＝∠C，

又∵AB＝CD，∠AFB＝∠CED，

∴（AAS）

【点睛】

本题考查了全等三角形的判定，熟练运用全等三角形的判定定理是本题的关键．

14．（2021·宁夏利通·八年级期末）如图，AD是△ABC中∠BAC的平分线，DE⊥AB交AB于点E，DF⊥AC交AC于点F．若S△ABC＝9，DE＝2，AB＝5，求AC的长．

【答案】AC＝4．

解：∵AD是△ABC中∠BAC的平分线，DE⊥AB于点E，DF⊥AC交AC于点F，

∴DF＝DE＝2．

又∵S△ABC＝S△ABD+S△ACD，AB＝5，

∴9＝×5×2+×AC×2，

∴AC＝4．

【点睛】

本题主要考查了角平分线的性质，角平分线的性质主要体现在垂线段相等，一般可作为某三角形的高处理三角形的面积问题．

15．（2021·陕西·西安市铁一中学八年级期末）如图，在△ABC中，AD平分∠BAC，∠C＝90°，DE⊥AB于点E，点F在AC上，BD＝DF．

（1）求证：CF＝EB；

（2）若AB＝14，AF＝8，求CF的长．

【答案】（1）见解析；（2）3

（1）∵DE⊥AB于点E，

∴∠DEB＝90°，

又AD平分∠BAC，∠C＝90°，

∴DC＝DE，

在Rt△DCF和Rt△DEB中，

，

∴Rt△DCF≌Rt△DEB（HL），

∴CF＝EB．

（2）在Rt△ACD和Rt△AED中，

，

∴Rt△ACD≌Rt△AED（HL），

∴AC＝AE，

设CF＝BE＝x，则AE＝AB﹣BE＝14﹣x，AC＝AF+CF＝8+x，

∴14﹣x＝8+x，解得：x＝3．

故CF＝3．

【点睛】

本题考查了全等三角形的判定与性质；角平分线的性质；解方程等知识，掌握这些知识并正确推理是关键，运用了方程思想．