

专题 17.15 勾股定理中考真题专练(培优篇)(专项练习)-八年级数学下册基础知识专项讲练(人教版)
展开专题 17.15 勾股定理中考真题专练(培优篇)(专项练习)
一、单选题
1.(2020·江苏南通·中考真题)如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A. B.2 C.2 D.3
2.(2020·内蒙古鄂尔多斯·中考真题)如图,在四边形ABCD中,,,,,分别以点A,C为圆心,大于长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为( )
A. B.6 C. D.8
3.(2011·山东枣庄·中考真题)如图,点的坐标是,若点在轴上,且是等腰三角形,则点的坐标不可能是( )
A.(2,0) B.(4,0)
C.(-,0) D.(3,0)
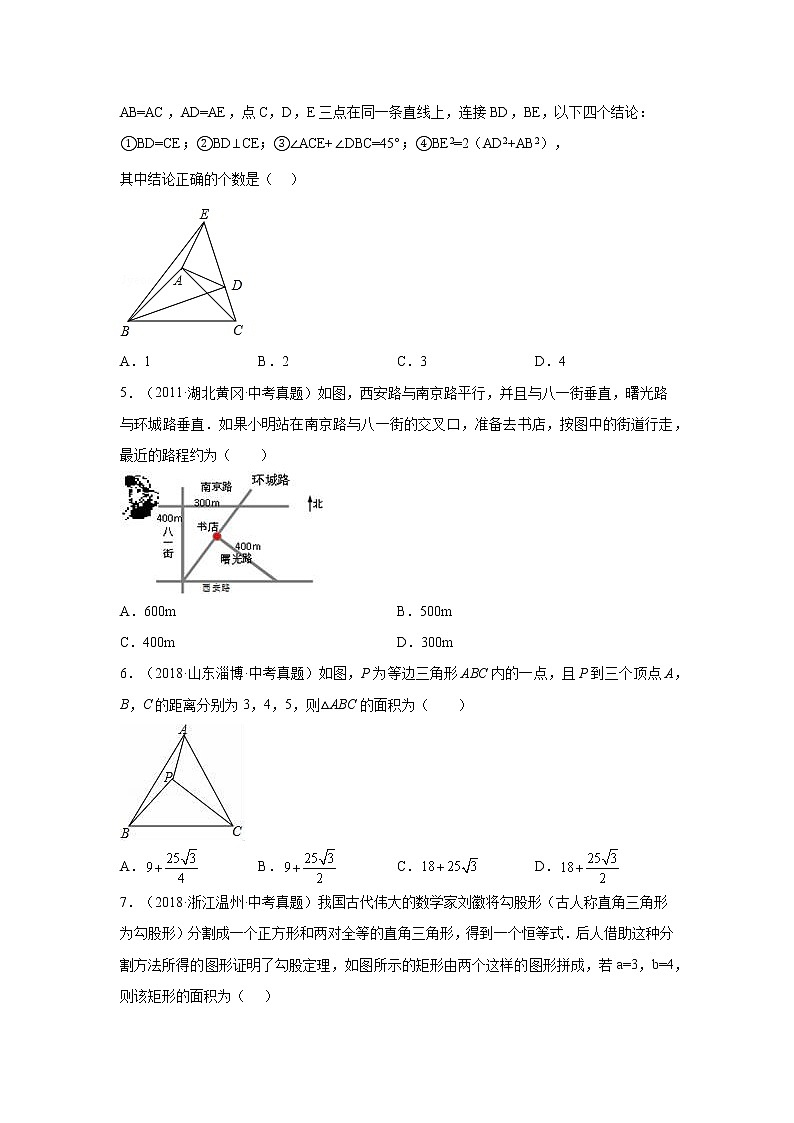
4.(2013·黑龙江绥化·中考真题)已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE,以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2),
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
5.(2011·湖北黄冈·中考真题)如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
A.600m B.500m
C.400m D.300m
6.(2018·山东淄博·中考真题)如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为( )
A. B. C. D.
7.(2018·浙江温州·中考真题)我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )
A.20 B.24 C. D.
二、填空题
8.(2020·湖北武汉·中考真题)如图,折叠矩形纸片,使点落在边的点处,为折痕,,.设的长为,用含有的式子表示四边形的面积是________.
9.(2020·天津·中考真题)如图,在每个小正方形的边长为1的网格中,的顶点均落在格点上,点B在网格线上,且.
(Ⅰ)线段的长等于___________;
(Ⅱ)以为直径的半圆与边相交于点D,若分别为边上的动点,当取得最小值时,请用无刻度的直尺,在如图所示的网格中,画出点,并简要说明点的位置是如何找到的(不要求证明).
10.(2020·贵州贵阳·中考真题)如图,中,点在边上,,,垂直于的延长线于点,,,则边的长为_____.
11.(2014·湖北武汉·中考真题)如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为_______.
12.(2018·四川资阳·中考真题)如图,在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,OA1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2018的坐标是_____.
13.(2018·黑龙江伊春·中考真题)如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.
14.(2018·浙江温州·中考真题)如图,直线与x轴、y轴分别交于A,B两点,C是OB的中点,D是AB上一点,四边形OEDC是菱形,则△OAE的面积为________.
15.(2016·福建南平·中考真题)如图,等腰ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将CAD与CBD分别沿直线CA、CB翻折得到CAP与CBQ,给出下列结论:
①CD=CP=CQ;
②∠PCQ的大小不变;
③PCQ面积的最小值为;
④当点D在AB的中点时,PDQ是等边三角形,其中所有正确结论的序号是______.
16.(2013·黑龙江·中考真题)已知等边三角形ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边三角形AB1C1,再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边三角形AB2C2,再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形,得到第三个等边AB3C3;…,如此下去,这样得到的第n个等边三角形ABnCn的面积为___.
三、解答题
17.(2018·黑龙江·中考真题)如图,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在直线于点F.
(1)当点E在线段BD上移动时,如图(1)所示,求证:BC﹣DE=DF.
(2)当点E在直线BD上移动时,如图(2)、图(3)所示,线段BC、DE与DF又有怎样的数量关系?请直接写出你的猜想,不需证明.
18.(2016·贵州六盘水·中考真题)在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图1,则有;若△ABC为锐角三角形时,小明猜想:,理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,,在Rt△ADB中,,∴.
∵a>0,x>0,∴2ax>0,∴,∴当△ABC为锐角三角形时.
所以小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时, 与的大小关系.
(2)温馨提示:在图3中,作BC边上的高.
(3)证明你猜想的结论是否正确.
19.(2006·江苏常州·中考真题)已知:如图,△ABC和△ECD都是等腰直角三角形,,D为AB边上一点,
求证:(1)△ACE≌△BCD;(2)
20.(2015·广西贵港·中考真题)已知:△ABC是等腰三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+,PA=,则:
①线段PB= ,PC= ;
②猜想:PA2,PB2,PQ2三者之间的数量关系为 ;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足,求的值.(提示:请利用备用图进行探求)
21. (2009·安徽芜湖·中考真题)如图,在梯形中,,.求的长.
参考答案
1.A
【解析】
【分析】
把要求的最大值的两条线段经过平移后形成一条线段,然后再根据垂线段最短来进行计算即可.
【详解】
解:如图,过点C作CK⊥l于点K,过点A作AH⊥BC于点H,
在Rt△AHB中,
∵∠ABC=60°,AB=2,
∴BH=1,AH=,
在Rt△AHC中,∠ACB=45°,
∴AC=,
∵点D为BC中点,
∴BD=CD,
在△BFD与△CKD中,
,
∴△BFD≌△CKD(AAS),
∴BF=CK,
延长AE,过点C作CN⊥AE于点N,
可得AE+BF=AE+CK=AE+EN=AN,
在Rt△ACN中,AN<AC,
当直线l⊥AC时,最大值为,
综上所述,AE+BF的最大值为.
故选:A.
【分析】本题主要考查了全等三角形的判定定理和性质定理及平移的性质,构建全等三角形是解答此题的关键.
2.A
【解析】
【分析】
连接FC,根据基本作图,可得OE垂直平分AC,由垂直平分线的性质得出AF=FC.再根据ASA证明△FOA≌△BOC,那么AF=BC=3,等量代换得到FC=AF=3,利用线段的和差关系求出FD=AD-AF=1.然后在直角△FDC中利用勾股定理求出CD的长.
【详解】
解:如图,连接FC,
∵点O是AC的中点,由作法可知,OE垂直平分AC,
∴AF=FC.
∵AD∥BC,
∴∠FAO=∠BCO.
在△FOA与△BOC中,
,
∴△FOA≌△BOC(ASA),
∴AF=BC=6,
∴FC=AF=6,FD=AD-AF=8-6=2.
在△FDC中,∵∠D=90°,
∴CD2+DF2=FC2,
∴CD2+22=62,
∴CD=.
故选:A.
【分析】本题考查了作图-基本作图,勾股定理,线段垂直平分线的判定与性质,全等三角形的判定与性质,难度适中.求出CF与DF是解题的关键.
3.D
【解析】
【详解】
解:(1)当点P在x轴正半轴上,
①以OA为腰时,
∵A的坐标是(2,2),
∴∠AOP=45°,OA=,
∴P的坐标是(4,0)或(,0);
②以OA为底边时,
∵点A的坐标是(2,2),
∴当点P的坐标为:(2,0)时,OP=AP;
(2)当点P在x轴负半轴上,
③以OA为腰时,
∵A的坐标是(2,2),
∴OA= ,
∴OA=AP=
∴P的坐标是(-,0).
故选D.
4.C
【解析】
【详解】
试题分析:①∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.
∵在△BAD和△CAE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△BAD≌△CAE(SAS).∴BD=CE.本结论正确.
②∵△BAD≌△CAE,∴∠ABD=∠ACE.
∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°.∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°.
∴BD⊥CE.本结论正确.
③∵△ABC为等腰直角三角形,∴∠ABC=∠ACB=45°.∴∠ABD+∠DBC=45°.
∵∠ABD=∠ACE,∴∠ACE+∠DBC=45°.本结论正确.
④∵BD⊥CE,∴在Rt△BDE中,利用勾股定理得:BE2=BD2+DE2.
∵△ADE为等腰直角三角形,∴DE=AD,即DE2=2AD2.
∴BE2=BD2+DE2=BD2+2AD2.
而BD2≠2AB2,本结论错误.
综上所述,正确的个数为3个.故选C.
5.B
【解析】
【分析】
由于BC∥AD,那么有∠DAE=∠ACB,由题意可知∠ABC=∠DEA=90°,BA=ED,利用AAS可证△ABC≌△DEA,于是AE=BC=300,再利用勾股定理可求AC,即可求CE,根据图可知从B到E的走法有两种,分别计算比较即可.
【详解】
解:如右图所示,
∵BC∥AD,
∴∠DAE=∠ACB,
又∵BC⊥AB,DE⊥AC,
∴∠ABC=∠DEA=90°,
又∵AB=DE=400m,
∴△ABC≌△DEA,
∴EA=BC=300m,
在Rt△ABC中,AC==500m,
∴CE=AC-AE=200,
从B到E有两种走法:①BA+AE=700m;②BC+CE=500m,
∴最近的路程是500m.
故选B.
【分析】本题考查了平行线的性质、全等三角形的判定和性质、勾股定理.解题的关键是证明△ABC≌△DEA,并能比较从B到E有两种走法.
6.A
【解析】
【详解】
分析:将△BPC绕点B逆时针旋转60°得△BEA,根据旋转的性质得BE=BP=4,AE=PC=5,∠PBE=60°,则△BPE为等边三角形,得到PE=PB=4,∠BPE=60°,在△AEP中,AE=5,延长BP,作AF⊥BP于点F.AP=3,PE=4,根据勾股定理的逆定理可得到△APE为直角三角形,且∠APE=90°,即可得到∠APB的度数,在直角△APF中利用三角函数求得AF和PF的长,则在直角△ABF中利用勾股定理求得AB的长,进而求得三角形ABC的面积.
详解:∵△ABC为等边三角形,
∴BA=BC,
可将△BPC绕点B逆时针旋转60°得△BEA,连EP,且延长BP,作AF⊥BP于点F.如图,
∴BE=BP=4,AE=PC=5,∠PBE=60°,
∴△BPE为等边三角形,
∴PE=PB=4,∠BPE=60°,
在△AEP中,AE=5,AP=3,PE=4,
∴AE2=PE2+PA2,
∴△APE为直角三角形,且∠APE=90°,
∴∠APB=90°+60°=150°.
∴∠APF=30°,
∴在直角△APF中,AF=AP=,PF=AP=.
∴在直角△ABF中,AB2=BF2+AF2=(4+)2+()2=25+12.
则△ABC的面积是•AB2=•(25+12)=9+.
故选A.
点睛:本题考查了等边三角形的判定与性质、勾股定理的逆定理以及旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.
7.B
【解析】
【分析】
设小正方形的边长为x,则矩形的一边长为(a+x),另一边为(b+x),根据矩形的面积的即等于两个三角形的面积之和,也等于长乘以宽,列出方程,化简再代入a,b的值,得出x2+7x=12,再根据矩形的面积公式,整体代入即可.
【详解】
设小正方形的边长为x,则矩形的一边长为(a+x),另一边为(b+x),根据题意得 :2(ax+x2+bx)=(a+x)(b+x),
化简得 :ax+x2+bx-ab=0,
又∵ a = 3 , b = 4 ,
∴x2+7x=12;
∴该矩形的面积为=(a+x)(b+x)=(3+x)(4+x)=x2+7x+12=24.
故答案为B.
【分析】本题考查了勾股定理的证明以及运用和一元二次方程的运用,求出小正方形的边长是解题的关键.
8.
【解析】
【分析】
首先根据题意可以设DE=EM=x,在三角形AEM中用勾股定理进一步可以用t表示出x,再可以设CF=y,连接MF,所以BF=2−y,在三角形MFN与三角形MFB中利用共用斜边,根据勾股定理可求出用t表示出y,进而根据四边形的面积公式可以求出答案.
【详解】
设DE=EM=x,
∴,
∴x= ,
设CF=y,连接FM,
∴BF=2−y,
又∵FN= y,NM=1,
∴,
∴y=,
∴四边形的面积为:=∙1,
故答案为:.
【分析】本题主要考查了勾股定理的综合运用,熟练掌握技巧性就可得出答案.
9.(1);(2)见解析
【解析】
【分析】
(1)将AC放在一个直角三角形,运用勾股定理求解;
(2)取格点M,N,连接MN,连接BD并延长,与MN相交于点;连接,与半圆相交于点E,连接BE,与AC相交于点P,连接并延长,与BC相交于点Q,则点P,Q即为所求.
【详解】
解:(Ⅰ)如图,在Rt△AEC中,CE=3,AE=2,则由勾股定理,得AC==;
(Ⅱ)如图,取格点M,N,连接MN,连接BD并延长,与MN相交于点;连接,与半圆相交于点E,连接BE,与AC相交于点P,连接并延长,与BC相交于点Q,则点P,Q即为所求.
【分析】本题考查作图-应用与设计,勾股定理,轴对称-最短问题,垂线段最短等知识,解题的关键是学会利用轴对称,根据垂线段最短解决最短问题,属于中考常考题型.
10.
【解析】
【分析】
如图,延长BD到点G,使DG=BD,连接CG,则由线段垂直平分线的性质可得CB=CG,在EG上截取EF=EC,连接CF,则∠EFC=∠ECF,∠G=∠CBE,根据等腰三角形的性质和三角形的内角和定理可得∠EFC=∠A=2∠CBE,再根据三角形的外角性质和等腰三角形的判定可得FC=FG,设CE=EF=x,则可根据线段间的和差关系求出DF的长,进而可求出FC的长,然后根据勾股定理即可求出CD的长,再一次运用勾股定理即可求出答案.
【详解】
解:如图,延长BD到点G,使DG=BD,连接CG,则CB=CG,在EG上截取EF=EC,连接CF,则∠EFC=∠ECF,∠G=∠CBE,
∵EA=EB,∴∠A=∠EBA,
∵∠AEB=∠CEF,
∴∠EFC=∠A=2∠CBE=2∠G,
∵∠EFC=∠G+∠FCG,
∴∠G=∠FCG,
∴FC=FG,
设CE=EF=x,则AE=BE=11-x,
∴DE=8-(11-x)=x-3,
∴DF=x-(x-3)=3,
∵DG=DB=8,
∴FG=5,∴CF=5,
在Rt△CDF中,根据勾股定理,得,
∴.
故答案为:.
【分析】本题考查了等腰三角形的判定和性质、三角形的内角和定理和三角形的外角性质、勾股定理以及线段垂直平分线的性质等知识,具有一定的难度,正确添加辅助线、灵活应用上述知识是解题的关键.
11..
【解析】
【详解】
作AD′⊥AD,AD′=AD,连接CD′,DD′,如图:
∵∠BAC+∠CAD=∠DAD′+∠CAD,
即∠BAD=∠CAD′,
在△BAD与△CAD′中,
,
∴△BAD≌△CAD′(SAS),
∴BD=CD′.
∠DAD′=90°
由勾股定理得DD′=,
∠D′DA+∠ADC=90°
由勾股定理得CD′=
∴BD=CD′=,
故答案为.
12.(0,21009)
【解析】
【详解】
【分析】本题点A坐标变化规律要分别从旋转次数与点A所在象限或坐标轴、点A到原点的距离与旋转次数的对应关系.
【详解】∵∠OAA1=90°,OA=AA1=1,以OA1为直角边作等腰Rt△OA1A2,再以OA2为直角边作等腰Rt△OA2A3,…,
∴OA1=,OA2=()2,…,OA2018=()2018,
∵A1、A2、…,每8个一循环,
∵2018=252×8+2
∴点A2018的在y轴正半轴上,OA2018==21009,
故答案为(0,21009).
【点睛】本题是平面直角坐标系下的规律探究题,除了研究动点变化的相关数据规律,还应该注意象限符号.
13.
【解析】
【详解】
【分析】由AB1是边长为2的等边三角形ABC的高,利用三线合一得到B1为BC的中点,求出CB1的长,继而可得△B1CB2是有一个角为30度的直角三角形,同理可知△B2C1B3、△B3C2B4、△B4C3B5、…、都是有一个角为30度的直角三角形,而且后一个的斜边是前一个30度角所邻的直角边,由此即可求得Sn.
【详解】∵等边三角形ABC的边长为2,AB1⊥BC,
∴∠C=60°,CB1=BB1=1,
又∵∠B1B2C=90°,∴∠CB1B2=30°,
∴CB2=,B1B2=,∴S1=,
同理,Rt△B2C1B3中,B2C1=B1B2=,∴C1B3=×=,B2B3=,
∴S2=,
同理,S3=
…,
∴Sn=,
故答案为.
【点睛】本题考查了规律题,涉及等边三角形的性质,含30度角的直角三角形的性质、勾股定理等,有一定难度,熟练掌握并灵活运用等边三角形的性质、勾股定理等解本题的关键.
14.
【解析】
【分析】
根据直线于坐标轴交点的坐标特点得出,A,B两点的坐标,得出OB,OA的长,根据C是OB的中点,从而得出OC的长,根据菱形的性质得出DE=OC=2;DE∥OC;设出D点的坐标,进而得出E点的坐标,从而得出EF,OF的长,在Rt△OEF中利用勾股定理建立关于x的方程,求解得出x的值,然后根据三角形的面积公式得出答案.
【详解】
解: 把x=0代入 y = − x + 4 得出y=4,
∴B(0,4);
∴OB=4;
∵C是OB的中点,
∴OC=2,
∵四边形OEDC是菱形,
∴DE=OC=2;DE∥OC,
把y=0代入 y = − x + 4 得出x=,
∴A(,0);
∴OA=,
设D(x,) ,
∴E(x,- x+2),
延长DE交OA于点F,
∴EF=-x+2,OF=x,
在Rt△OEF中利用勾股定理得:,
解得 :x1=0(舍),x2=;
∴EF=1,
∴S△AOE=·OA·EF=2.
故答案为.
【分析】本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.也考查了菱形的性质.
15.①②④.
【解析】
【分析】
【详解】
①∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,
∴CP=CD=CQ,∴①正确;
②∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,∴∠ACP=∠ACD,∠BCQ=∠BCD,
∴∠ACP+∠BCQ=∠ACD+∠BCD=∠ACB=120°,
∴∠PCQ=360°﹣(∠ACP+BCQ+∠ACB)
=360°﹣(120°+120°)
=120°,
∴∠PCQ的大小不变;∴②正确;
③如图,过点Q作QE⊥PC交PC延长线于E,
∵∠PCQ=120°,
∴∠QCE=60°,
在Rt△QCE中,tan∠QCE=,
∴QE=CQ×tan∠QCE=CQ×tan60°=CQ,
∵CP=CD=CQ,
∴S△PCQ=CP×QE=CP×CQ=,
∴CD最短时,S△PCQ最小,即:CD⊥AB时,CD最短,
过点C作CF⊥AB,此时CF就是最短的CD,
∵AC=BC=4,∠ACB=120°,
∴∠ABC=30°,
∴CF=BC=2,即:CD最短为2,
∴S△PCQ最小===,∴③错误;
④∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,
∴AD=AP,∠DAC=∠PAC,
∵∠DAC=30°,
∴∠APD=60°,
∴△APD是等边三角形,
∴PD=AD,∠ADP=60°,同理:△BDQ是等边三角形,
∴DQ=BD,∠BDQ=60°,
∴∠PDQ=60°,
∵当点D在AB的中点,
∴AD=BD,
∴PD=DQ,
∴△DPQ是等边三角形,
∴④正确,
故答案为①②④.
考点:几何变换综合题;定值问题;最值问题;综合题;翻折变换(折叠问题).
16.
【解析】
【详解】
由AB1为边长为2等边三角形ABC的高,利用三线合一得到B1为BC的中点,求出BB1的长,利用勾股定理求出AB1的长,进而求出第一个等边三角形AB1C1的面积,同理求出第二个等边三角形AB2C2的面积,依此类推,得到第n个等边三角形ABnCn的面积.
解:∵等边三角形ABC的边长为2,AB1⊥BC,
∴BB1=1,AB=2,
根据勾股定理得:AB1=,
∴第一个等边三角形AB1C1的面积为×()2=()1;
∵等边三角形AB1C1的边长为,AB2⊥B1C1,
∴B1B2=,AB1=,
根据勾股定理得:AB2=,
∴第二个等边三角形AB2C2的面积为×()2=()2;
依此类推,第n个等边三角形ABnCn的面积为()n.
故答案为()n
17.(1)证明见解析;(2)如图2:DE﹣BC=DF;图3:BC+DE=DF.
【解析】
【详解】
【分析】(1)如图1中,在BA上截取BH,使得BH=BE.构造全等三角形即可解决问题;
(2)如图2中,在BC上截取BH=BE,同法可证:DF=EH.可得:DE﹣BC=DF.如图3中,在BA上截取BH,使得BH=BE.同法可证:DF=HE,可得BC+DE=DF.
【详解】(1)如图1中,在BA上截取BH,使得BH=BE.
∵BC=AB=BD,BE=BH,
∴AH=ED,
∵∠AEF=∠ABE=90°,
∴∠AEB+∠FED=90°,∠AEB+∠BAE=90°,
∴∠FED=∠HAE,
∵∠BHE=∠CDB=45°,
∴∠AHE=∠EDF=135°,
∴△AHE≌△EDF,
∴HE=DF,
∴BC﹣DE=BD﹣DE=BE=EH=DF.
∴BC﹣DE=DF.
(2)如图2中,在BC上截取BH=BE,同法可证:DF=EH.
可得:DE﹣BC=DF;
如图3中,在BA上截取BH,使得BH=BE.同法可证:DF=HE,
可得BC+DE=DF.
【点睛】本题考查了全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
18.(1);(2)作图见解析;(3)正确.
【解析】
【分析】
(1)根据题意可猜测:当△ABC为钝角三角形时,与的大小关系为:;
(2)根据题意可作辅助线:过点A作AD⊥BC于点D;
(3)然后设CD=x,分别在Rt△ADC与Rt△ADB中,表示出AD2,即可证得结论.
【详解】
解:(1)当△ABC为钝角三角形时,与的大小关系为:;
(2)如图3,过点A作AD⊥BC于点D;
(3)证明:如图3,设CD=x.在Rt△ADC中,,在Rt△ADB中,,
∴.
∵a>0,x>0,
∴2ax>0,
∴,
∴当△ABC为钝角三角形时,.
考点:三角形综合题;勾股定理.
19.(1) ∵
∴
即
∵
∴ △BCD≌△ACE
(2)∵ ,
∴
∵ △BCD≌△ACE
∴
∴
∴
【解析】
【详解】
(1)本题要判定△ACE≌△BCD,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,则DC=EA,AC=BC,∠ACB=∠ECD,又因为两角有一个公共的角∠ACD,所以∠BCD=∠ACE,根据SAS得出△ACE≌△BCD.
(2)由(1)的论证结果得出∠DAE=90°,AE=DB,从而求出AD2+DB2=DE2.
20.(1)①,2;②;(2)证明见试题解析;(3)或.
【解析】
【详解】
试题分析:
(1)①由已知条件求出AB的长,再减去PA就可得PB的长;如图1,连接BQ,先证△APC≌△BQC,可得:BQ=AP=,∠CBQ=∠A=45°,由此可得△PBQ是直角三角形,即可计算出PQ=,从而根据△PCQ是等腰直角三角形可得PC=2;
②由①中的证明可知:AP=BQ,△PBQ是直角三角形,由此即可得到:PB2+BQ2=AP2+PB2=PQ2;
(2)如图2,连接PB,先证△APC≌△BQC,得到BQ=AP,∠CBQ=∠A=45°,由此可得△PBQ是直角三角形,从而可得:PB2+BQ2=PB2+AP2=PQ2,即(1)中所猜想结论仍然成立;
(3)如图3,分点P在点A、B之间和在点A、B的同侧两种情况讨论即可;
试题解析:
(1)如图①:
①∵△ABC是等腰直直角三角形,AC=1+,∠ACB=90°,
∴AB=,
∵PA=,
∴PB=AB-PA=.
∵△ABC和△PCQ均为以点C为直角顶点的等腰直角三角形,
∴AC=BC,PC=CQ,∠ACP=∠BCQ,
∴△APC≌△BQC.
∴BQ=AP=,∠CBQ=∠A=45°.
∴△PBQ为直角三角形.
∴PQ=.
∴PC=PQ=2.
故答案为,2;
②如图1,猜想PA2+PB2=PQ2,理由如下:
由①中证明可知:△APC≌△BQC,
∴BQ=AP,∠CBQ=∠A=45°,
又∵∠CBA=45°,
∴∠CBQ+∠CBA=∠PCQ=90°,
∴BQ2+PB2=PQ2,
∴PA2+PB2=PQ2.
(2)如图②:连接BQ,
∵△ABC和△PCQ均为以点C为直角顶点的等腰直角三角形,
∴AC=BC,PC=CQ,∠ACP=∠BCQ,
∴△APC≌△BQC.
∴BQ=AP,∠CBQ=∠A=45°.
又∵∠ABC=45°,
∴∠ABC+∠CBQ=∠ABQ=90°,
∴∠PBQ=90°,
∴在Rt△PBQ中,BQ2+PB2=PQ2,
∴PA2+PB2=PQ2.
(3)如图③:过点C作CD⊥AB,垂足为D.由△ABC中,∠ACB=90°,AC=BC可得:AD=BD=CD=AB;设AB=,则AD=BD=CD=,
①当点P位于点A、D之间的点P1处时.
∵,
∴P1A=AB=DC= ,
∴P1D=AD=,
在Rt△CP1D中,由勾股定理得:CP1=,
在Rt△ACD中,由勾股定理得:AC= ,
∴;
②当点P位于点A和点B的同侧的点P2处时.
∵,
∴P2A=AB=AD=.
∴P2D=P2A+AD=,
在Rt△CP2D中,由勾股定理得:P2C=,
在Rt△ACD中,由勾股定理得:AC=,
∴;
综上所述,的比值为或.
点睛:(1)本题第1小题②问和第2小题的解题要点是一致的,就是连接BQ,利用等腰直角三角形的性质证得△APC≌△BQC,得到PA=QB,∠CBQ=∠CAP=45°,就可把PA、PB、BQ三条分散的线段集中到Rt△PBQ中,由勾股定理就可得到三条线段间的数量关系;(2)讨论本题第3小题时,需注意点P的位置存在两种情形,讨论时不要忽略了其中任何一种.
21.解:作于于
四边形是矩形.
是的边上的中线.
在中,
【解析】
【详解】
作于于先证四边形是矩形,根据矩形的对边相等即直角三角形斜边的中线等于斜边的一半求得DF、AE、BE,再根据勾股定理即可求出AB.
初中数学人教版八年级下册17.1 勾股定理课时作业: 这是一份初中数学人教版八年级下册<a href="/sx/tb_c10261_t7/?tag_id=28" target="_blank">17.1 勾股定理课时作业</a>,共32页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学人教版八年级下册17.1 勾股定理当堂检测题: 这是一份初中数学人教版八年级下册<a href="/sx/tb_c10261_t7/?tag_id=28" target="_blank">17.1 勾股定理当堂检测题</a>,共27页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理课堂检测: 这是一份初中数学人教版八年级下册<a href="/sx/tb_c10261_t7/?tag_id=28" target="_blank">第十七章 勾股定理17.1 勾股定理课堂检测</a>,共28页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













