安徽省亳州市利辛县向阳中学2022-2023学年七年级数学上册第三次月考测试题(含答案)

安徽省亳州市利辛县向阳中学2022-2023学年七年级数学上册第三次月考测试题（附答案）

一、选择题（本大题共10小题，总计40分）

1．﹣12021的相反数是（　　）

A．2021 B．﹣2021 C．1 D．﹣1

2．如图，将三角形绕轴旋转一周，所得的立体图形从正面观察得到的图形是（　　）

A．B． C．   D．

3．“东风快递，使命必达！”东风﹣41是我国目前最先进的洲际战略导弹，假设其最快飞行速度是25马赫，若每马赫速度为340米/秒，则用科学记数法表示东风﹣41的最快飞行速度为（　　）

A．8.5×103米/秒 B．0.85×104米/秒 

C．8.5×104米/秒 D．85×103米/秒

4．在式子，﹣4x，abc，π，，0.81，，0中，单项式共有（　　）

A．5个 B．6个 C．7个 D．8个

5．若x＝3t+1，y＝2t﹣1，用含y的式子表示x的结果是（　　）

A． B． C． D．

6．某市举办中学生足球赛，按比赛规则，每场比赛都要分出胜负，胜1场得3分，负一场扣1分，菁英中学队在8场比赛中得到12分，若设该队胜的场数为x，负的场数为y，则可列方程组为（　　）

A． B． 

C． D．

7．下列叙述正确的有（　　）个．

①射线AB的端点是A和B；②各边相等，各角也相等的多边形叫做正多边形；

③连接两点的线段叫做两点的距离；

④两点之间线段最短．

A．1 B．2 C．3 D．4

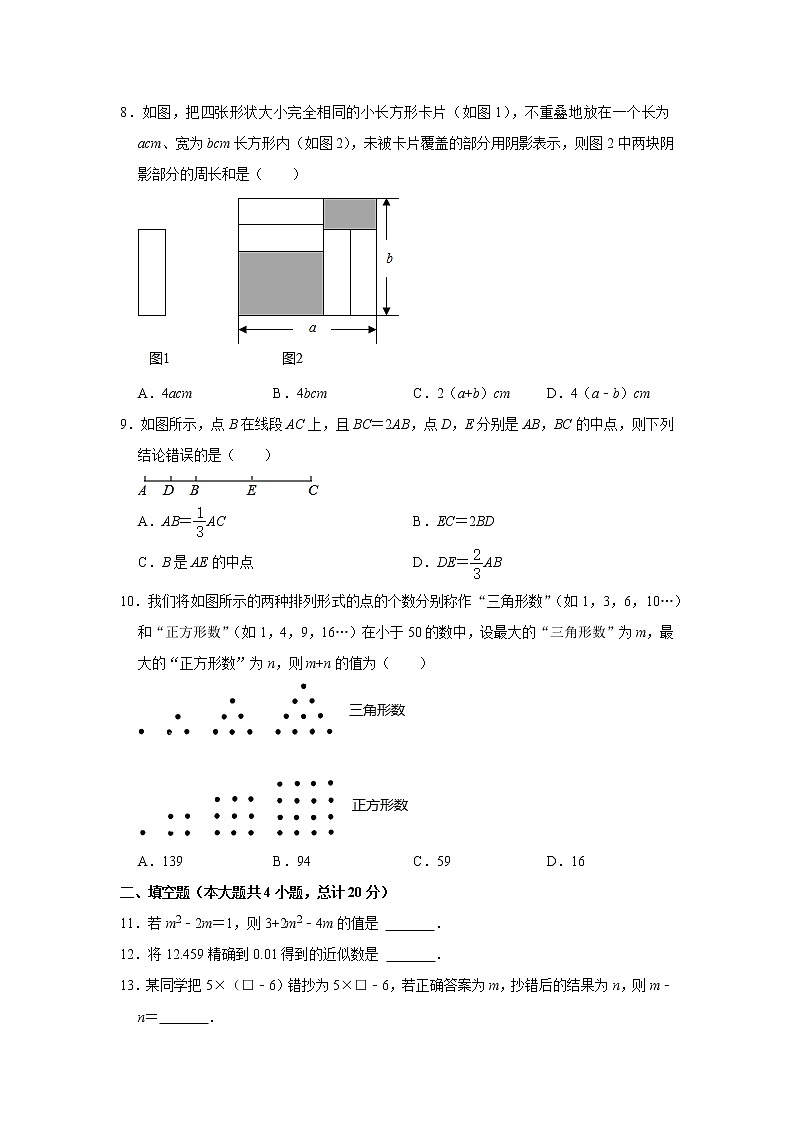
8．如图，把四张形状大小完全相同的小长方形卡片（如图1），不重叠地放在一个长为acm、宽为bcm长方形内（如图2），未被卡片覆盖的部分用阴影表示，则图2中两块阴影部分的周长和是（　　）

A．4acm B．4bcm C．2（a+b）cm D．4（a﹣b）cm

9．如图所示，点B在线段AC上，且BC＝2AB，点D，E分别是AB，BC的中点，则下列结论错误的是（　　）

A．AB＝AC B．EC＝2BD 

C．B是AE的中点 D．DE＝AB

10．我们将如图所示的两种排列形式的点的个数分别称作“三角形数”（如1，3，6，10…）和“正方形数”（如1，4，9，16…）在小于50的数中，设最大的“三角形数”为m，最大的“正方形数”为n，则m+n的值为（　　）

A．139 B．94 C．59 D．16

二、填空题（本大题共4小题，总计20分）

11．若m2﹣2m＝1，则3+2m2﹣4m的值是 　   　．

12．将12.459精确到0.01得到的近似数是 　   　．

13．某同学把5×（□﹣6）错抄为5×□﹣6，若正确答案为m，抄错后的结果为n，则m﹣n＝　   　．

14．《九章算术》中有一道阐述“盈不足术”的问题，原文如下：

今有共买物，人出八，盈三；人出七，不足四．问人数、物价各几何？

意思是：几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价值是多少？

该问题中物品的价值是 　   　钱．

三、计算题（本大题共2小题，总计16分）

15．计算：

（1）3+（﹣2）+（﹣4）．

（2）．

16．解方程及方程组：

（1）．

（2）．

四、解答题（本大题共7小题，总计74分）

17．如图，已知直线l和直线外A，B，C三点，按下列要求画图：

（1）画射线AB；

（2）连接BC，延长BC至点D使得CD＝BC；

（3）在直线l上确定点E，使得点E到点A，点C的距离之和最短．

18．先化简，再求值：5x2﹣[2xy﹣3（）+5x2]，其中|2x﹣1|+（3y+2）2＝0．

19．商场将每件进价为90元的某种商品原来按每件110元出售，一天可售出100件．后经过市场调查，发现这种商品单价每降低1元，其销量可增加10件．为使顾客尽可能得到实惠，当每件商品售价定为多少元时，商场经营该商品一天可获利2210元？

20．将7张相同的小长方形纸片（如图1所示）按图2所示的方式不重叠的放在长方形ABCD内，未被覆盖的部分恰好被分割为两个长方形，面积分别为S1，S2，已知小长方形纸片的长为a＝9，宽为b＝2，且a＞b，AD＝30．

请求：

（1）长方形ABCD的面积；

（2）S1﹣S2的值．

21．如图，AB＝24cm，C、D点在线段AB上，且CD＝10cm，M、N分别是AC、BD的中点，求线段MN的长．

22．【问题背景】我们知道|x|的几何意义是：在数轴上数x对应的点与原点O的距离，这个结论可以推广为：|x1﹣x2|表示在数轴上数x1，x2对应点之间的距离．如图①，在数轴上，点A，B，O，C，D的位置如图所示，则DC＝|3﹣1|＝2；CO＝|1﹣0|＝1；AB＝|（﹣4）﹣（﹣2）|＝|﹣2|＝2．

【问题解决】

（1）计算|2﹣（﹣3）|＝　   　．

（2）如果点A为数轴上一点，它所表示的数为x，点B在数轴上表示的数为﹣4，|AB|＝5，那么x为 　   　．

【关联运用】

（1）运用一：代数式|x﹣1|+|x+4|的最小值为 　   　．

（2）运用二：在图②，点A，B、C是数轴上的三点，A点表示数是﹣3，B点表示数是﹣1，C点表示数是6，点A，B，C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和3个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC．则AB＝　   　，AC＝　   　．（用含t的代数式表示）

（3）在（2）的条件下，若mAC﹣4AB的值不随着时间t的变化而改变，试确定m的值．

23．（操作）结合图形，完成以下填空：

（1）点C1在线段AB上，如图1，图中有 　   　条线段；

（2）点C1，C2在线段AB上，如图2，图中有 　   　条线段；

（3）点C1，C2，C3在线段AB上，如图3，图中有 　   　条线段；

（猜想）点C1，C2，C3，……，∁n在线段AB上，如图4，图中有 　   　条线段（用含n的代数式表示）．

（应用）春节期间，10位同学之间互通电话（每两位同学之间只通一次电话）祝福，求10位同学之间通电话的次数．

参考答案

一、选择题（本大题共10小题，总计40分）

1．解：﹣12021＝﹣1，﹣1的相反数是1．

故选：C．

2．解：将三角形绕轴旋转一周，所得的立体图形是圆锥体，而圆锥体从正面观察得到的图形是等腰三角形，

故选：A．

3．解：340×25＝8500＝8.5×103（米/秒）．

故选：A．

4．解：式子，﹣4x，abc，π，0.81，0是单项式，共6个，

故选：B．

5．解：∵y＝2t﹣1，

∴t＝，

把t的值代入x＝3t+1，得x＝3×+1，即x＝，

故选：B．

6．解：依题意得：．

故选：C．

7．解：①射线AB和射线BA的端点不同，故不是同一条射线，故错误；

②各边相等，各角也相等的多边形叫做正多边形，故正确；

③连接两点的线段的长叫做两点间的距离，故错误；

④两点之间，线段最短，故正确．

故选：B．

8．解：如图：

设小长方形卡片的宽为t，则AB＝CD＝（b﹣2t）cm，BC＝AD＝（a﹣2t）cm，EF＝GH＝2tcm，

∵HN＝ME＝BC＝（a﹣2t）cm，

∴FH＝b﹣HN＝b﹣（a﹣2t）＝b﹣a+2t＝EG，

∴两块阴影部分的周长和是：2AB+2BC+2EF+2FH＝2（b﹣2t）+2（a﹣2t）+2×2t+2（b﹣a+2t）＝4bcm，

故选：B．

9．解：A．由BC＝2AB，AC＝AB+BC，得：AC＝3AB，即AB＝AC，故正确；

B．由D，E分别是AB，BC的中点，得：EC＝BE＝AB＝2BD，故正确；

C．由E分别是BC的中点，BC＝2AB，得BE＝AB，所以B是AE的中点，故正确；

D．由上述结论，得：DE＝DB+BE＝AB+AB＝AB，故错误．

故选：D．

10．解：∵“三角形数”分别是1，3，6，10，…，

∴第x个“三角形数“，

∵＜50，且x为正整数，

∴x取最大值9，

∴m＝45，

∵“正方形数”分别是1，4，9，16，…，

∴第y个“正方形数”y2，y为正整数，

∵y2＜50，

∴y取最大值7，

∴n＝49，

∴m+n＝94，

故选：B．

二、填空题（本大题共4小题，总计20分）

11．解：原式＝3+2（m2﹣2m）

＝3+2×1

＝3+2

＝5．

故答案为：5．

12．解：12.459精确到0.01得到的近似数是12.46．

故答案为：12.46．

13．解：由题意可得，

5×（□﹣6）＝m，5×□﹣6＝n，

∴m﹣n

＝5×（□﹣6）﹣（5×□﹣6）

＝5□﹣30﹣5□+6

＝﹣24，

故答案为：﹣24．

14．解：设有x人，物品的价值为y钱，

依题意，得：，

解得：，

即该问题中物品的价值是53钱，

故答案为：53．

三、计算题（本大题共2小题，总计16分）

15．解：（1）3+（﹣2）+（﹣4）＝﹣3．

（2）

＝﹣1﹣24+1

＝﹣24．

16．解：（1）去分母得：3（x﹣2）＝12﹣2（4﹣3x），

去括号得：3x﹣6＝12﹣8+6x，

移项合并得：3x＝﹣10，

系数化为1得：x＝﹣；

（2），

②×2﹣①得：3x＝﹣3，

解得：x＝﹣1，

把x＝﹣1代入②得：﹣2+y＝2，

解得：y＝4，

则方程组的解为．

四、解答题（本大题共7小题，总计74分）

17．解：（1）如图，射线AB即为所求．

（2）如图，线段BC，线段CD即为所求．

（3）如图，点E即为所求．

18．解：原式＝5x2﹣2xy+3（）﹣5x2

＝5x2﹣2xy+xy+6﹣5x2

＝﹣xy+6，

∵|2x﹣1|+（3y+2）2＝0，

∴2x﹣1＝0，3y+2＝0，

解得：x＝，y＝﹣，

∴原式＝﹣×（﹣）+6

＝6．

19．解：设该商品每件降价x元，商场一天可获利润2210元，

依题意得：

（110﹣90﹣x）（100+10x）＝2210，

解得：x1＝3，x2＝7．

∵要使顾客尽可能得到实惠，

∴x＝7，

∴每件商品售价应定为110﹣7＝103（元），

答：商店经营该商品一天要获利润2210元，每件商品售价定为103元．

20．解：（1）由图可知，

AB＝4b+a＝4×2+9＝8+9＝17，

又∵AD＝30，

∴S长方形ABCD＝AB•AD＝17×30＝510；

（2）由图可得，

S1﹣S2

＝（4b•AD﹣4ab）﹣（a•AD﹣3ab）

＝（4×2×30﹣4×9×2）﹣（9×30﹣3×9×2）

＝（240﹣72）﹣（270﹣54）

＝168﹣216

＝﹣48．

21．解：∵AB＝24cm，CD＝10cm，

∴AC+BD＝AB﹣CD＝14cm，

∵M、N分别是AC、BD的中点，

∴CM＝AC，DN＝BD，

∴CM+DN＝AC+BD＝7cm，

∵CD＝10cm，

∴MN＝CM+DN+CD＝7cm+10cm＝17cm．

22．解：【问题解决】（1）|2﹣（﹣3）|＝|2+3|＝+5+＝5，

故答案为：5；

（2）由题可知，AB＝|x﹣（﹣4）|＝|x+4|，

∴|x+4|＝5，解得x＝﹣9或1，

故答案为：﹣9或1；

【关联运用】（1）代数式|x﹣1|+|x+4|表示数轴上数x所对应的点到数1和﹣4所对应的点的距离之和，

需要分以下三种情况：

由上图形可知，代数式|x﹣1|+|x+4|的最小值为5，

故答案为：5；

（2）由点的运动可知，运动后点A，点B，点C所表示的数分别为：﹣3﹣t，﹣1+2t，6+3t，

∴AB＝﹣1+2t﹣（﹣3﹣t）＝﹣1+2t+3+t＝2+3t，

AC＝6+3t﹣（﹣3﹣t）＝6+3t+3+t＝9+4t，

故答案为：2+3t，9+4t；

（3）由（2）知AB＝2+3t，AC＝9+4t，

∴mAC﹣4AB＝m（9+4t）﹣4（2+3t）＝9m+4mt﹣8﹣12t＝（4m﹣12）t+9m﹣8，

∵mAC﹣4AB的值不随着时间t的变化而改变，

∴4m﹣12＝0，解得m＝3．

23．解：（1）点C1在线段AB上，图1中的线段有：1+2＝3（条）；

故答案为：3；

（2）点C1，C2在线段AB上，图2中的线段有：1+2+3＝6（条）；

故答案为：6；

（3）点C1，C2，C3在线段AB上，图3中的线段有：1+2+3+4＝10（条）；

猜想：点C1，C2，C3，……，∁n在线段AB上，图4中的线段有：1+2+3+…+n+（n+1）＝；

故答案为：10，；

应用：（次）．

答：10位同学之间通电话的次数为45．