2023年中考数学（苏科版）总复习一轮课时训练 18　全等三角形(含答案)

这是一份2023年中考数学（苏科版）总复习一轮课时训练 18　全等三角形(含答案)，共9页。
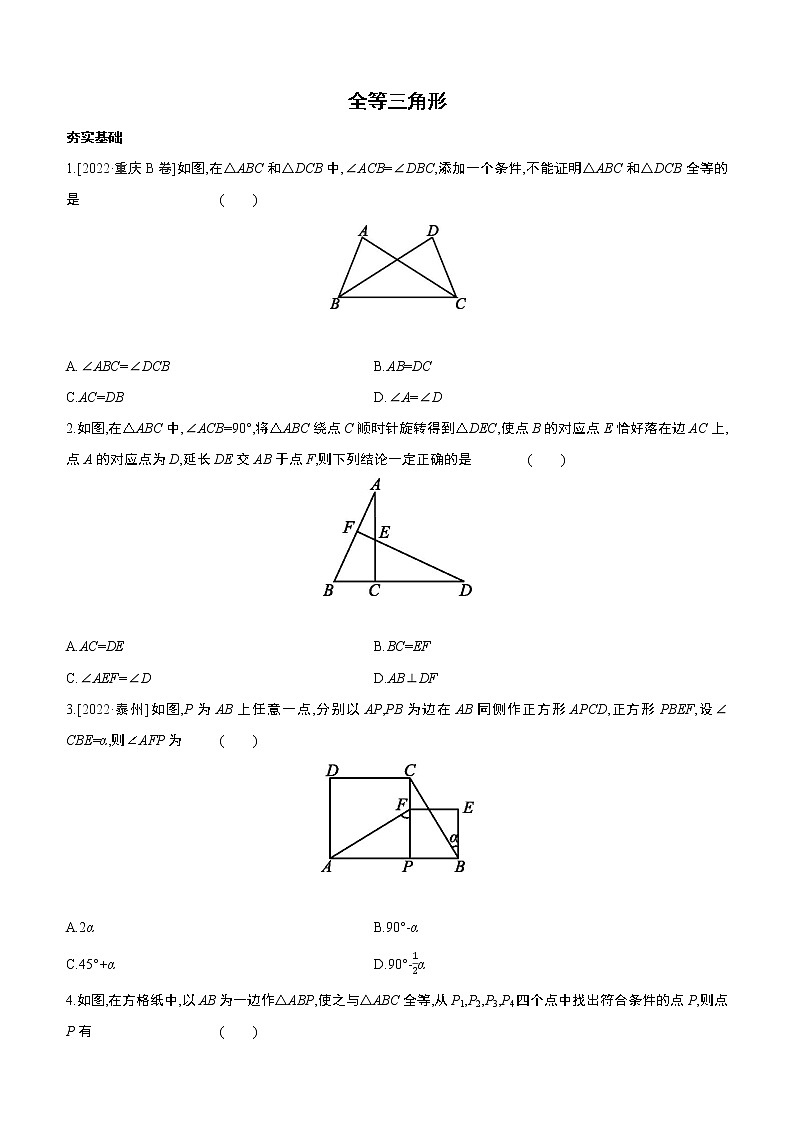
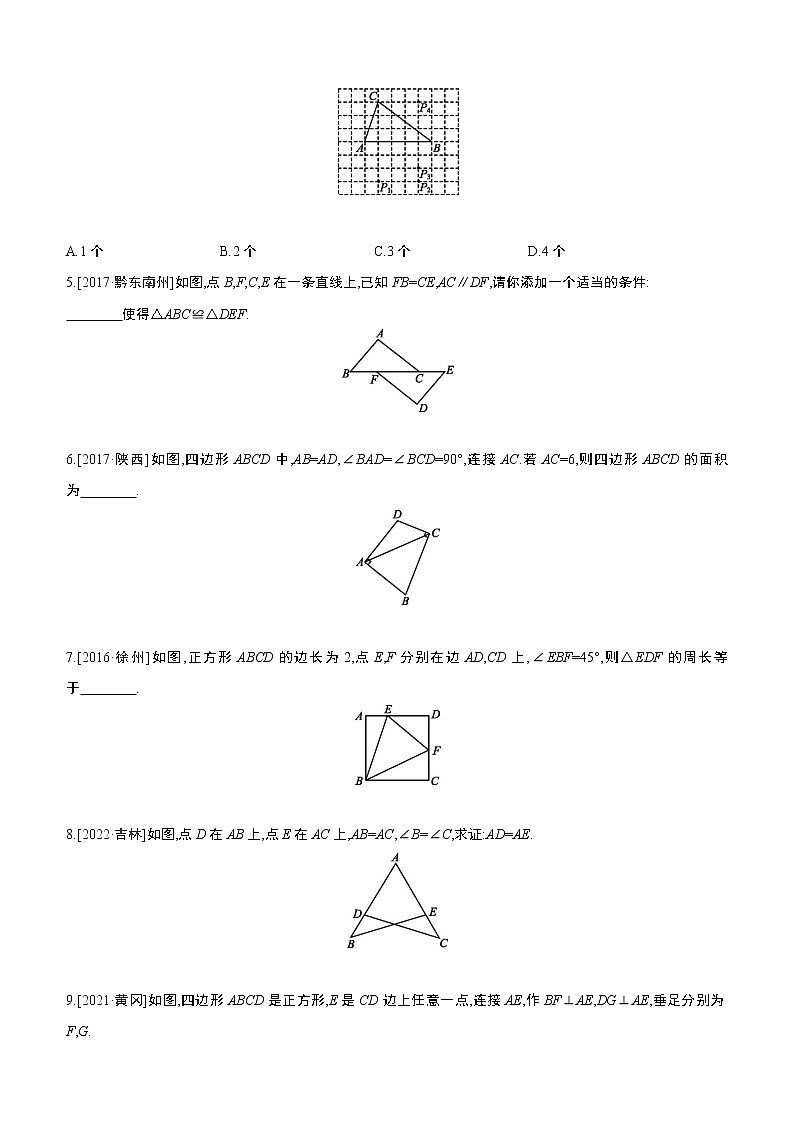
全等三角形夯实基础1.[2022·重庆B卷]如图,在△ABC和△DCB中,∠ACB=∠DBC,添加一个条件,不能证明△ABC和△DCB全等的是              (　　) A.∠ABC=∠DCB  B.AB=DCC.AC=DB  D.∠A=∠D2.如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是              (　　) A.AC=DE  B.BC=EFC.∠AEF=∠D  D.AB⊥DF3.[2022·泰州]如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD,正方形PBEF,设∠CBE=α,则∠AFP为              (　　) A.2α  B.90°-αC.45°+α  D.90°-α4.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有              (    ) A.1个 B.2个 C.3个 D.4个5.[2017·黔东南州]如图,点B,F,C,E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件:　　　　使得△ABC≌△DEF.  6.[2017·陕西]如图,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为　　　　.  7.[2016·徐州]如图,正方形ABCD的边长为2,点E,F分别在边AD,CD上,∠EBF=45°,则△EDF的周长等于　　　　.  8.[2022·吉林]如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:AD=AE. 9.[2021·黄冈]如图,四边形ABCD是正方形,E是CD边上任意一点,连接AE,作BF⊥AE,DG⊥AE,垂足分别为F,G.求证:BF-DG=FG.    10.[2022·黄石]如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于E点,DE=EF.(1)求证:△ADE≌△CFE;(2)若AB=5,CF=4,求BD的长.  11.[2022·南京]如图,AC与BD交于点O,OA=OD,∠ABO=∠DCO,E为BC延长线上一点,过点E作EF∥CD,交BD的延长线于点F.(1)求证:△AOB≌△DOC;(2)若AB=2,BC=3,CE=1,求EF的长.   12.[2021·镇江]如图,四边形ABCD中,AD∥BC,点E,F分别在AD,BC上,AE=CF,过点A,C分别作EF的垂线,垂足分别为G,H.(1)求证:△AGE≌△CHF;(2)连接AC,线段GH与AC是否互相平分?请说明理由.  拓展提升13.如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形.连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q.连接PQ,BM.下列结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有              () A.1个 B.2个 C.3个 D.4个14.[2022·泰安]如图,在平行四边形ABCD中,E是BD的中点,则下列四个结论: ①AM=CN;②若MD=AM,∠A=90°,则BM=CM;③若MD=2AM,则S△MNC=S△BNE;④若AB=MN,则△MFN与△DFC全等.其中正确结论的个数为 (　　)A.1个 B.2个 C.3个 D.4个15.[2021·苏州]问题1:如图①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,∠APD=90°.求证:AB+CD=BC.问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°.求的值.答案1.B　在△ABC和△DCB中,∠ACB=∠DBC,BC=BC,A.当∠ABC=∠DCB时,△ABC≌△DCB(ASA),故A能证明;B.当AB=DC时,不能证明两三角形全等,故B不能证明;C.当AC=DB时,△ABC≌△DCB(SAS),故C能证明;D.当∠A=∠D时,△ABC≌△DCB(AAS),故D能证明.故选:B.2.D3.B　∵四边形PBEF为正方形,∴∠PBE=90°,∵∠CBE=α,∴∠PBC=90°-α,∵四边形APCD,四边形PBEF都是正方形,∴AP=CP,∠APF=∠CPB=90°,PF=PB,在△APF和△CPB中,∴△APF≌△CPB(SAS),∴∠AFP=∠PBC=90°-α.4.C　 将△ABC沿着直线AB翻折可得△ABP1,将△ABP1进行轴对称变换可得△ABP2,再将△ABP2沿着直线AB进行翻折,可得△ABP4,故满足条件的点P共有3个.故选C.5.答案不唯一,例如AC=FD,∠B=∠E等6.18　过点A作AE⊥AC交CD的延长线于点E,由题意易证△AED≌△ACB,故AE=AC=6,四边形ABCD的面积等于△ACE的面积,即四边形ABCD的面积=AC×AE=×6×6=18.7.4　如图,延长线段DA至点G,使得AG=CF,连接BG,则可证△BCF≌△BAG,所以BG=BF,因为∠EBF=45°,则可证△GBE≌△FBE,所以EF=GE,由正方形边长为2可求出△EDF的周长为4.8.证明:在△ABE和△ACD中,∴△ABE≌△ACD(ASA),∴AD=AE.9.证明:在△ABF和△DAG中,∵BF⊥AE,DG⊥AE,∴∠AFB=∠DGA=90°.又∠DAG+∠FAB=∠DAG+∠ADG=90°,∴∠FAB=∠GDA.又AB=AD,∴△ABF≌△DAG.∴BF=AG,AF=DG.∴BF-DG=AG-AF=FG.10.解:(1)证明:∵AB∥FC,∴∠ADE=∠F,在△ADE和△CFE中,∴△ADE≌△CFE(ASA).(2)由(1)得△ADE≌△CFE,∴AD=CF,∴BD=AB-AD=AB-CF=5-4=1.11.解:(1)证明:在△AOB和△DOC中,∴△AOB≌△DOC(AAS).(2)由(1)得:△AOB≌△DOC,∴AB=DC=2,∵BC=3,CE=1,∴BE=BC+CE=4,∵EF∥CD,∴△BCD∽△BEF,∴,即,解得:EF=.12.解:(1)证明:∵AG⊥EF,CH⊥EF,∴∠G=∠H=90°,AG∥CH.∵AD∥BC,∴∠DEF=∠BFE,∵∠AEG=∠DEF,∠CFH=∠BFE,∴∠AEG=∠CFH.在△AGE和△CHF中,∴△AGE≌△CHF(AAS).(2)线段GH与AC互相平分,理由如下:连接AH,CG,如图所示:由(1)得:△AGE≌△CHF,∴AG=CH,∵AG∥CH,∴四边形AHCG是平行四边形,∴线段GH与AC互相平分.13.D　∵△ABD,△BCE均为等边三角形,∴AB=DB,∠ABD=∠CBE=60°,BE=BC,∴∠ABE=∠DBC,∠PBQ=60°.在△ABE和△DBC中,∴△ABE≌△DBC(SAS),①正确;∵△ABE≌△DBC,∴∠BAE=∠BDC.∵∠BDC+∠BCD=180°-60°-60°=60°,∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°,②正确;在△ABP和△DBQ中,∴△ABP≌△DBQ(ASA),∴BP=BQ,∴△BPQ为等边三角形,③正确;∵∠DMA=60°,∴∠AMC=120°,∴∠AMC+∠PBQ=180°,∴P,B,Q,M四点共圆.∵BP=BQ,∴,∴∠BMP=∠BMQ,即MB平分∠AMC,④正确.综上所述,正确的结论有4个,故选D.14.D　①∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠ADB=∠CBD,∵E是BD的中点,∴BE=DE,在△MDE和△NBE中,∴△MDE≌△NBE(ASA),∴DM=BN,∴AM=CN,故①正确;②若MD=AM,∠A=90°,则平行四边形ABCD为矩形,∴∠ADC=∠A=90°,在△BAM和△CDM中,∴△BAM≌△CDM(SAS),∴BM=CM,故②正确;③过点M作MG⊥BC,交BC于G,过点E作EH⊥BC,交BC于H,由①可知四边形MBND是平行四边形,E为BD中点,∴E也为MN中点,∴MG=2EH,又∵MD=2AM,BN=MD,AM=NC,∴S△MNC=NC·MG=·BN·2EH=BN·EH=S△BNE,故③正确;④∵AB=MN,AB=DC,∴MN=DC,又∵AD∥BC,∴四边形MNCD是等腰梯形或平行四边形,如果四边形MNCD是等腰梯形,则∠MNC=∠DCN,在△MNC和△DCN中,∴△MNC≌△DCN(SAS),∴∠NMC=∠CDN,在△MFN和△DFC中,∴△MFN≌△DFC(AAS),如果是平行四边形,由平行四边形的性质可以得到△MFN≌△CFD,故④正确.15.解:问题1:证法一:∵∠B=90°,∴∠APB+∠BAP=90°.∵∠APD=90°,∴∠APB+∠CPD=90°.∴∠BAP=∠CPD.在△ABP和△PCD中,∴△ABP≌△PCD(AAS).∴AB=PC,BP=CD,∴AB+CD=BP+PC=BC.证法二:由证法一,可设∠BAP=∠CPD=α.在Rt△ABP中,BP=PA·sinα,AB=PA·cosα,在Rt△PCD中,CD=PD·sinα,PC=PD·cosα,又∵PA=PD,∴AB=PC,BP=CD,∴AB+CD=BP+PC=BC.问题2:如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.由问题1可知AE+DF=EF,在Rt△ABE和Rt△DFC中,∠B=∠C=45°,∴AE=BE,DF=CF,AB=AE,CD=DF.∴BC=BE+EF+CF=2(AE+DF),AB+CD=(AE+DF).∴.