浙江省温州市第二中学2022-2023学年八年级上学期期中数学试卷(含答案)

这是一份浙江省温州市第二中学2022-2023学年八年级上学期期中数学试卷(含答案)，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
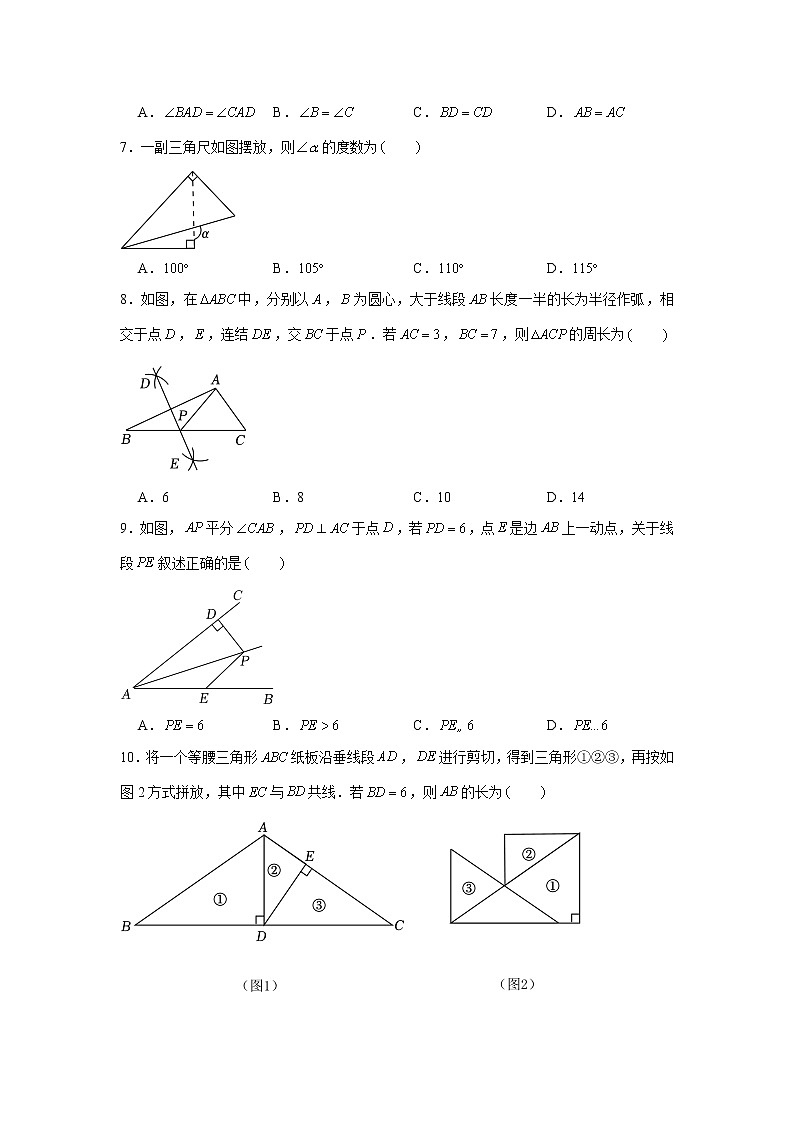
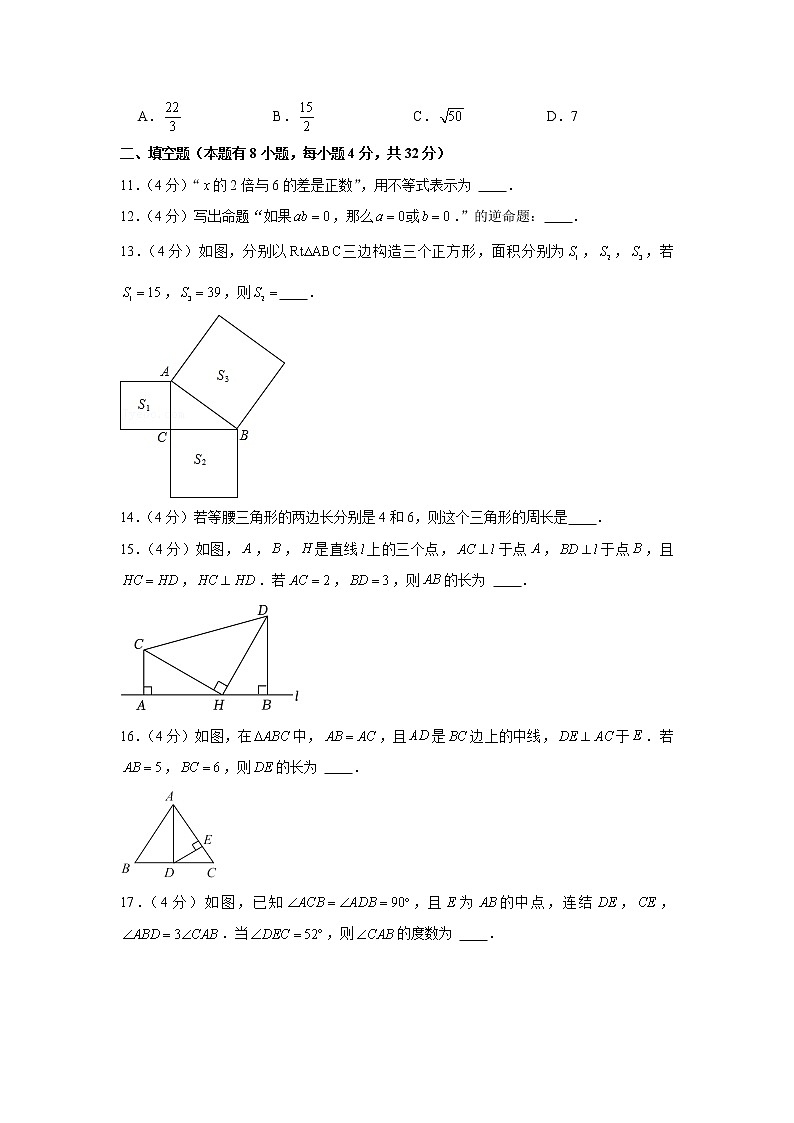
2022-2023学年浙江省温州二中八年级（上）期中数学试卷一、选择题（本题有10小题，每小题3分，共30分）1．下列图形中，是轴对称图形的是　　A． B． C． D．2．如图所示，在数轴上表示不等式正确的是　　A． B． C． D．3．若一个三角形的两边长分别是2和4，则第三边长可能是　　A．1 B．2 C．4 D．64．下列条件中，能判定为直角三角形的是　　A． B． C． D．，5．对于命题“如果，那么”，能说明它是假命题的反例是　　A． B． C． D．6．如图，已知，补充下列哪一个条件，仍不能判定和全等的是　　A． B． C． D．7．一副三角尺如图摆放，则的度数为　　A． B． C． D．8．如图，在中，分别以，为圆心，大于线段长度一半的长为半径作弧，相交于点，，连结，交于点．若，，则的周长为　　A．6 B．8 C．10 D．149．如图，平分，于点，若，点是边上一动点，关于线段叙述正确的是　　A． B． C． D．10．将一个等腰三角形纸板沿垂线段，进行剪切，得到三角形①②③，再按如图2方式拼放，其中与共线．若，则的长为　　A． B． C． D．7二、填空题（本题有8小题，每小题4分，共32分）11．（4分）“的2倍与6的差是正数”，用不等式表示为 　　．12．（4分）写出命题“如果，那么或．”的逆命题：　　．13．（4分）如图，分别以三边构造三个正方形，面积分别为，，，若，，则　　．14．（4分）若等腰三角形的两边长分别是4和6，则这个三角形的周长是　　．15．（4分）如图，，，是直线上的三个点，于点，于点，且，．若，，则的长为 　　．16．（4分）如图，在中，，且是边上的中线，于．若，，则的长为 　　．17．（4分）如图，已知，且为的中点，连结，，．当，则的度数为 　　．18．（4分）研究任务画出平分三角形面积的一条直线研究成果中线法中线法 是边上的中线 若，则．成果应用如图，在中， 是边上的中线，直线平分的面积，交于点．已知，的面积为10，则　　，四边形的面积为 　　．三、解答题（本题有6小题，共58分）19．（8分）如图，中，，，与的平分线交于点，过做分别交，于点，．求的周长．请补全以下的解答过程．解：平分（已知），（角平分线的定义），又（已知），　　　　，　　，　　　　．同理可得：　　．的周长　　　　．20．（6分）当时，（1）请比较与的大小，并说明理由．（2）若，则的取值范围为 　　．（直接写出答案）21．（8分）在下列网格中，每个小正方形的边长均为1．请按要求画出格点三角形．（1）在图1中画出一个等腰．（2）在图2中画出一个，且其三边都不与网格线重合．22．（10分）如图，已知，相交于点，且，．（1）求证：．（2）若，求的度数．23．（12分）等边中，点，分别是边，上的点，且，，交于点．（1）求证：．（2）求的度数．（3）若，，则的面积为 　　．（直接写出答案）24．（14分）如图1，在长方形中，，，动点从点出发，沿边，向点运动．（1）当点在边上，且时，求的度数．（2）当的面积为20时，求的长．（3）如图2，若，关于直线对称．①连结，，当点在边上时，求的面积．②当直线恰好经过点时，请直接写出的长度． 
2022-2023学年浙江省温州二中八年级（上）期中数学试卷参考答案与试题解析一、选择题（本题有10小题，每小题3分，共30分）1．【解答】解：，，选项中的图形都不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；选项中的图形能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；故选：．2．【解答】解：由题意，得：，故选：．3．【解答】解：设第三边的长为，由题意得：，即，观察选项，只有选项符合题意．故选：．4．【解答】解：．由无法得到为直角三角形，故本选项符合题意；．，，无法得到为直角三角形，故本选项符合题意；．，，最大角，是直角三角形，故本选项符合题意；．，，，，，不是直角三角形，故本选项不符合题意．故选：．5．【解答】解：当时，满足条件，但不能得出的结论，能说明命题“如果，那么”是假命题的反例是，故选：．6．【解答】解：，，，添加，，故选项不符合题意；添加，，故选项不符合题意；添加，，故选项不符合题意；添加，不能判定，故选项符合题意，故选：．7．【解答】解：如图，由题意得：，，，，．故选：．8．【解答】解：由作法得垂直平分，，的周长．故选：．9．【解答】解：过点作于，如图，平分，，，，点是边上一动点，．故选：．10．【解答】解：如图，设为，为，为，图2中的余角为，为等腰三角形，，，，，，结合两图，可得，设为，根据勾股定理得，，解得：，，故选：．二、填空题（本题有8小题，每小题4分，共32分）11．【解答】解：“的2倍与6的差是正数”用不等式表示为，故答案为：．12．【解答】解：命题“如果，那么或．”的逆命题是如果或，那么，故答案为：如果或，那么．13．【解答】解：由勾股定理得：，，．故答案为：24．14．【解答】解：①若4为腰，满足构成三角形的条件，周长为；②若6为腰，满足构成三角形的条件，则周长为．故答案为：14或16．15．【解答】解：于点，于点，，，，在和中，，，，，，的长为5，故答案为：5．16．【解答】解：在中，，且是边上的中线，，，在中，由勾股定理得，，，，，故答案为：．17．【解答】解：设，，，，且为的中点，，，，，，，，，，的度数为．故答案为：．18．【解答】解：如图，连接与，由研究成果可知，，，设的面积为，则的面积为，，，，的面积为，，，四边形的面积．故答案为：3，．三、解答题（本题有6小题，共58分）19．【解答】解：平分（已知），（角平分线的定义），又（已知），（两直线平行，内错角相等），，（等腰三角形的判定）．同理可得：．的周长．故答案为：，两直线平行，内错角相等；，，等腰三角形的判定；，，．20．【解答】解：（1），理由是：，，，；（2），，，，即的取值范围是．故答案为：．21．【解答】解：（1）根据等腰三角形的定义画出图形即可；（2）根据直角三角形的定义画出图形即可．22．【解答】（1）证明：在与中，，；（2），，又，．23．【解答】（1）证明：为等边三角形，，，在和中，，；（2）解：由（1）可知：，，；（3）解：过点作交的延长线于，，，，由勾股定理得：，，故答案为：．24．【解答】解：（1）四边形为长方形，故，，当时，则，为等腰直角三角形，； （2）当点在上时，的面积为长方形面积的一半，即30，当的面积为20时，点在上，则的面积，解得：，； （3）①，关于直线对称，故，而，则的面积； ②当点在上时，如（图， 在中，，，则，则，则，在中，；当点在上时，如（图， 由题意得：，，，，在中，，，则，则，，则，，则，在中，，则，综上，的长度为8或．