安徽省合肥市第五十中学2022-2023学年九年级上学期期中考试数学试题(含答案)

2022-2023学年安徽省合肥五十中九年级（上）期中数学试卷

一、选择题（每小题4分，共40分）

1．（4分）将抛物线y＝x2向上平移3个单位，所得抛物线的解析式是（　　）

A．y＝x2+3 B．y＝x2﹣3 C．y＝（x+3）2 D．y＝（x﹣3）2

2．（4分）对于二次函数y＝（x﹣1）2+2的图象，下列说法正确的是（　　）

A．开口向下 B．对称轴是直线x＝﹣1 

C．顶点坐标是（1，2） D．与x轴有两个交点

3．（4分）如图，在△ABC中，D为AB上的一点，过点D作DE∥BC交AC于点E，过点D作DF∥AC交BC 于点F，则下列结论错误的是（　　）

A．＝ B．＝ C．＝ D．＝

4．（4分）如图，已知P是△ABC边AB上的一点，连接CP．以下条件中不能判定△ACP∽△ABC的是（　　）

A．∠ACP＝∠B B．∠APC＝∠ACB C．AC2＝AP•AB D．＝

5．（4分）△ABC的三边长分别为2，3，4，另有一个与它相似的三角形DEF，其最长边为12，则△DEF的周长是（　　）

A．54 B．36 C．27 D．21

6．（4分）已知二次函数y＝x2﹣2x﹣3的自变量x1，x2，x3对应的函数值分别为y1，y2，y3.当﹣1＜x1＜0，1＜x2＜2，x3＞3时，y1，y2，y3三者之间的大小关系是（　　）

A．y1＜y2＜y3 B．y2＜y1＜y3 C．y3＜y1＜y2 D．y2＜y3＜y1

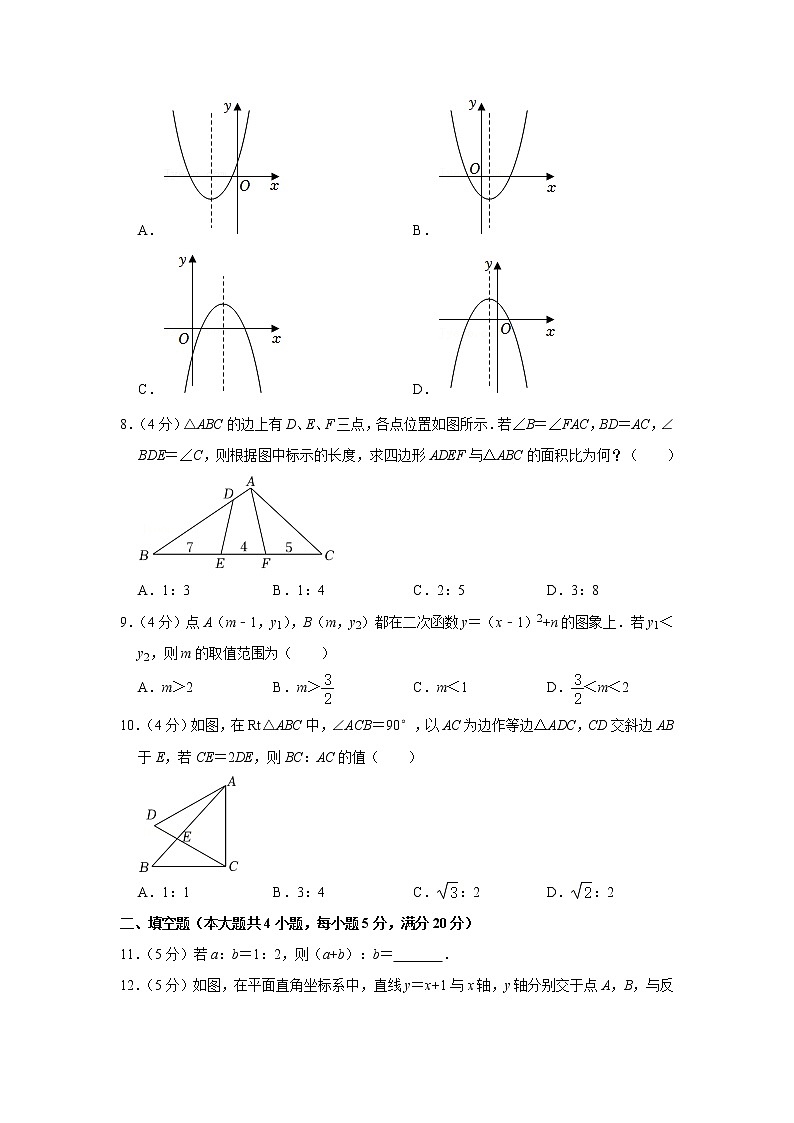
7．（4分）已知二次函数y＝ax2+bx﹣c（a≠0），其中b＞0、c＞0，则该函数的图象可能为（　　）

A． B． 

C． D．

8．（4分）△ABC的边上有D、E、F三点，各点位置如图所示．若∠B＝∠FAC，BD＝AC，∠BDE＝∠C，则根据图中标示的长度，求四边形ADEF与△ABC的面积比为何？（　　）

A．1：3 B．1：4 C．2：5 D．3：8

9．（4分）点A（m﹣1，y1），B（m，y2）都在二次函数y＝（x﹣1）2+n的图象上．若y1＜y2，则m的取值范围为（　　）

A．m＞2 B．m＞ C．m＜1 D．＜m＜2

10．（4分）如图，在Rt△ABC中，∠ACB＝90°，以AC为边作等边△ADC，CD交斜边AB于E，若CE＝2DE，则BC：AC的值（　　）

A．1：1 B．3：4 C．：2 D．：2

二、填空题（本大题共4小题，每小题5分，满分20分）

11．（5分）若a：b＝1：2，则（a+b）：b＝　   　．

12．（5分）如图，在平面直角坐标系中，直线y＝x+1与x轴，y轴分别交于点A，B，与反比例函数y＝的图象在第一象限交于点C，若AB＝BC，则k的值为 　   　．

13．（5分）如图，在Rt△ABC中，∠C＝90°，棱长为1的立方体的表面展开图有两条边分别在AC，BC上，有两个顶点在斜边AB上，则△ABC的面积为 　   　．

14．（5分）已知k为任意实数，随着k的变化，抛物线y＝x2﹣2（k﹣1）x+k2﹣3的顶点随之运动，则顶点运动时经过的路径与两条坐标轴围成图形的面积是 　   　．

三、（本大题共2小题，每小题8分，满分16分）

15．（8分）已知某抛物线过点A（2，0），对称轴为x＝4，顶点在直线y＝x﹣1上，求此抛物线的解析式．

16．（8分）如图，△ABC中，点E、F分别在边AB、AC上，∠1＝∠2．若BC＝4，AF＝2，CF＝3，求EF的长．

四、（本大题共2小题，每小题8分，满分16分）

17．（8分）在如图的正方形格点纸中，每个小的四边形都是边长为1的正方形，A、B、C、D、F，H都是格点，AB与CD相交于O，AH与CD相交于E，求AO与BO的比值．

18．（8分）在平面直角坐标系中，如果一个点的横坐标与纵坐标互为相反数，则称该点为“黎点”．例如（﹣1，1），（2022，﹣2022）都是“黎点”．

（1）求双曲线y＝上的“黎点”；

（2）若抛物线y＝ax2﹣7x+c（a、c为常数）上有且只有一个“黎点”，当a＞1时，求c的取值范围．

五、（本大题共2小题，每小题10分，满分20分）

19．（10分）对于抛物线y＝x2﹣2x﹣3．

（1）它与x轴交点的坐标为 　   　，顶点坐标为 　   　；

（2）在下面的坐标系中利用描点法画出此抛物线；

（3）利用以上信息解答下列问题：若关于x的一元二次方程x2﹣2x﹣3﹣t＝0（t为实数）在0＜x＜4的范围内有解，则t的取值范围是 　   　.（直接写出结果）

20．（10分）如图，在等边三角形ABC中，D、E分别在AC、AB上，且，AE＝BE．

（1）求证△AED∽△CBD；

（2）已知△BDC的面积为，求BD长．

六、（本题满分12分）

21．（12分）如图，在平面直角坐标系xOy中，正方形ABCO的对角线BO在x轴上，若正方形ABCO的边长为2，点B在x轴负半轴上，反比例函数y＝的图象经过C点．

（1）求该反比例函数的解析式；

（2）当函数值y＞﹣2时，请直接写出自变量x的取值范围；

（3）若点P是反比例函数上的一点，且△PBO的面积恰好等于正方形ABCO的面积，求点P的坐标．

七、（本题满分12分）

22．（12分）如图是甲、乙两人进行羽毛球练习赛时的一个瞬间，羽毛球飞行的高度y（m）与水平距离x（m）的路线为抛物线的一部分，如图，甲在O点正上方1m的P处发出一球，已知点O与球网的水平距离为5m，球网的高度为1.55m．羽毛球沿水平方向运动4m时，达到羽毛球距离地面最大高度是m．

（1）求羽毛球经过的路线对应的函数关系式；

（2）通过计算判断此球能否过网；

（3）若甲发球过网后，羽毛球飞行到离地面的高度为m的Q处时，乙扣球成功求此时乙与球网的水平距离．

八、（本题满分14分）

23．（14分）如图，矩形ABCD中，点E在DC上，DE＝BE，AC与BD相交于点O，BE与AC相交于点F．

（1）若BE平分∠CBD，求证：BF⊥AC；

（2）找出图中与△OBF相似的三角形，并说明理由；

（3）若OF＝3，EF＝2，求DE的长度．

2022-2023学年安徽省合肥五十中九年级（上）期中数学试卷

参考答案与试题解析

一、选择题（每小题4分，共40分）

1．（4分）将抛物线y＝x2向上平移3个单位，所得抛物线的解析式是（　　）

A．y＝x2+3 B．y＝x2﹣3 C．y＝（x+3）2 D．y＝（x﹣3）2

【分析】根据二次函数变化规律：左加右减，上加下减，进而得出变化后解析式．

【解答】解：∵抛物线y＝x2向上平移3个单位，

∴平移后的解析式为：y＝x2+3．

故选：A．

【点评】此题考查了抛物线的平移以及抛物线解析式的性质，熟练记忆平移规律是解题关键．

2．（4分）对于二次函数y＝（x﹣1）2+2的图象，下列说法正确的是（　　）

A．开口向下 B．对称轴是直线x＝﹣1 

C．顶点坐标是（1，2） D．与x轴有两个交点

【分析】根据抛物线的性质由a＝1得到图象开口向上，根据顶点式得到顶点坐标为（1，2），对称轴为直线x＝1，从而可判断抛物线与x轴没有公共点．

【解答】解：二次函数y＝（x﹣1）2+2的图象开口向上，顶点坐标为（1，2），对称轴为直线x＝1，抛物线与x轴没有公共点．

故选：C．

【点评】本题考查了二次函数的性质：二次函数y＝ax2+bx+c（a≠0）的顶点式为y＝a（x﹣）2+，的顶点坐标是（﹣，），对称轴直线x＝﹣b2a，当a＞0时，抛物线y＝ax2+bx+c（a≠0）的开口向上，当a＜0时，抛物线y＝ax2+bx+c（a≠0）的开口向下．

3．（4分）如图，在△ABC中，D为AB上的一点，过点D作DE∥BC交AC于点E，过点D作DF∥AC交BC 于点F，则下列结论错误的是（　　）

A．＝ B．＝ C．＝ D．＝

【分析】根据平行线分线段成比例定理得出比例式，再把它们等量代换，即可得出答案．

【解答】解：∵DF∥AC，

∴＝，

∵DE∥BC，

∴四边形DECF为平行四边形，

∴DE＝CF，

∴＝，故A正确；

∵DE∥BC，

∴＝，故B正确；

∵DE∥BC，DF∥AC，

∴＝，＝，故C错误；

∵DE∥BC，DF∥AC，

∴＝，＝，

∴＝，故D正确；

故选：C．

【点评】本题考查了平行线分线段成比例定理，此题比较简单，注意掌握比例线段的对应关系是解此题的关键．

4．（4分）如图，已知P是△ABC边AB上的一点，连接CP．以下条件中不能判定△ACP∽△ABC的是（　　）

A．∠ACP＝∠B B．∠APC＝∠ACB C．AC2＝AP•AB D．＝

【分析】根据题目中各个选项可以判断哪个选项中的说法是错误的，从而可以解答本题．

【解答】解：∵∠ACP＝∠B，∠CAP＝∠BAC，

∴△ACP∽△ABC，故选项A正确；

∵∠APC＝∠ACB，∠CAP＝∠BAC，

∴△ACP∽△ABC，故选项B正确；

∵AC2＝AP•AB，

∴，

又∵∠CAP＝∠BAC，

∴△ACP∽△ABC，故选项C正确；

∵，

但未说明∠ACP＝∠ABC，

∴不能判断△ACP∽△ABC，故选项D错误；

故选：D．

【点评】本题考查相似三角形的判定，解题的关键是明确相似三角形的判定．

5．（4分）△ABC的三边长分别为2，3，4，另有一个与它相似的三角形DEF，其最长边为12，则△DEF的周长是（　　）

A．54 B．36 C．27 D．21

【分析】（1）方法一：设2对应的边是x，3对应的边是y，根据相似三角形的对应边的比相等列等式，解出即可；

方式二：根据相似三角形的周长的比等于相似比，列出等式计算．

【解答】解：方法一：设2对应的边是x，3对应的边是y，

∵△ABC∽△DEF，

∴＝＝，

∴x＝6，y＝9，

∴△DEF的周长是27；

方式二：∵△ABC∽△DEF，

∴＝，

∴＝，

∴C△DEF＝27；

故选：C．

【点评】本题考查了相似三角形的性质，掌握相似三角形的性质的应用是解题关键．

6．（4分）已知二次函数y＝x2﹣2x﹣3的自变量x1，x2，x3对应的函数值分别为y1，y2，y3.当﹣1＜x1＜0，1＜x2＜2，x3＞3时，y1，y2，y3三者之间的大小关系是（　　）

A．y1＜y2＜y3 B．y2＜y1＜y3 C．y3＜y1＜y2 D．y2＜y3＜y1

【分析】首先求出抛物线开口方向和对称轴，然后根据二次函数的增减性即可解决问题．

【解答】解：∵抛物线y＝x2﹣2x﹣3＝（x﹣1）2﹣4，

∴抛物线开口向上，对称轴x＝1，顶点坐标为（1，﹣4），

当y＝0时，（x﹣1）2﹣4＝0，

解得x＝﹣1或x＝3，

∴抛物线与x轴的两个交点坐标为：（﹣1，0），（3，0），

∴当﹣1＜x1＜0，1＜x2＜2，x3＞3时，y2＜y1＜y3，

故选：B．

【点评】本题考查抛物线的性质，熟练掌握抛物线的性质是解决问题的关键，记住在抛物线的左右函数的增减性不同，确定对称轴的位置是关键，属于中考常考题型．

7．（4分）已知二次函数y＝ax2+bx﹣c（a≠0），其中b＞0、c＞0，则该函数的图象可能为（　　）

A． B． 

C． D．

【分析】根据c＞0，可知﹣c＜0，可排除A，D选项，当a＞0时，可知对称轴＜0，可排除B选项，当a＜0时，可知对称轴＞0，可知C选项符合题意．

【解答】解：∵c＞0，

∴﹣c＜0，

故A，D选项不符合题意；

当a＞0时，

∵b＞0，

∴对称轴x＝＜0，

故B选项不符合题意；

当a＜0时，b＞0，

∴对称轴x＝＞0，

故C选项符合题意，

故选：C．

【点评】本题考查了二次函数的图象，熟练掌握二次函数的图象与系数的关系是解题的关键．

8．（4分）△ABC的边上有D、E、F三点，各点位置如图所示．若∠B＝∠FAC，BD＝AC，∠BDE＝∠C，则根据图中标示的长度，求四边形ADEF与△ABC的面积比为何？（　　）

A．1：3 B．1：4 C．2：5 D．3：8

【分析】证明△CAF∽△CBA，推出CA2＝CF•CB，推出AC＝4，可得＝＝，推出S△ACF：S△ACB＝5：16，同法S△BDE：S△ABC＝5：16，由此可得结论．

【解答】解：∵∠C＝∠C，∠CAF＝∠B，

∴△CAF∽△CBA，

∴＝，

∴CA2＝CF•CB，

∴CA2＝5×16＝80，

∵AC＞0，

∴AC＝4，

∴＝＝，

∴S△ACF：S△ACB＝5：16，

同法可证△BDE∽△BCA，

∵BD＝AC，

∴＝，

∴S△BDE：S△ABC＝5：16，

∴S四边形ADEF：S△ABC＝（16﹣5﹣5）：16＝3：8，

故选：D．

【点评】本题考查相似三角形的判定和性质，解题的关键是正确寻找相似三角形解决问题，属于中考选择题中的压轴题．

9．（4分）点A（m﹣1，y1），B（m，y2）都在二次函数y＝（x﹣1）2+n的图象上．若y1＜y2，则m的取值范围为（　　）

A．m＞2 B．m＞ C．m＜1 D．＜m＜2

【分析】根据y1＜y2列出关于m的不等式即可解得答案．

【解答】解：∵点A（m﹣1，y1），B（m，y2）都在二次函数y＝（x﹣1）2+n的图象上，

∴y1＝（m﹣1﹣1）2+n＝（m﹣2）2+n，

y2＝（m﹣1）2+n，

∵y1＜y2，

∴（m﹣2）2+n＜（m﹣1）2+n，

∴（m﹣2）2﹣（m﹣1）2＜0，

即﹣2m+3＜0，

∴m＞，

故选：B．

【点评】本题考查了二次函数图象上点的坐标特征，解题的关键是根据已知列出关于m的不等式．本题属于基础题，难度不大．

10．（4分）如图，在Rt△ABC中，∠ACB＝90°，以AC为边作等边△ADC，CD交斜边AB于E，若CE＝2DE，则BC：AC的值（　　）

A．1：1 B．3：4 C．：2 D．：2

【分析】如图，过点D作DJ⊥AC于点J交AB于点K．首先证明DJ＝BC，再利用＝，可得结论．

【解答】解：如图，过点D作DJ⊥AC于点J交AB于点K．

∵△ADC是等边三角形，DJ⊥AC，

∴AJ＝JC，

∵∠AJD＝∠ACB＝90°，

∴JK∥CB，

∴AK＝KB，

∵DK∥CB，

∴＝＝＝，

∵AK＝KB，AJ＝JC，

∴KJ＝BC，

∴DJ＝BC，

∵∠DJA＝90°，∠DAJ＝60°

∴＝tan60°＝，

∴＝，

∴＝．

故选：C．

【点评】本题考查平行线分线段成比例定理，等边三角形的性质等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题．

二、填空题（本大题共4小题，每小题5分，满分20分）

11．（5分）若a：b＝1：2，则（a+b）：b＝　3：2　．

【分析】根据比例设a＝k，b＝2k，再代入代数式进行计算即可得解．

【解答】解：∵a：b＝1：2，

∴可设a＝k，b＝2k，

∴（a+b）：b＝（k+2k）：2k＝3：2，

故答案为：3：2．

【点评】本题考查了比例的性质．已知几个量的比值时，常用的解法是：设一个未知数，把题目中的几个量用所设的未知数表示出来，实现消元．

12．（5分）如图，在平面直角坐标系中，直线y＝x+1与x轴，y轴分别交于点A，B，与反比例函数y＝的图象在第一象限交于点C，若AB＝BC，则k的值为 　2　．

【分析】过点C作CH⊥x轴于点H．求出点C的坐标，可得结论．

【解答】解：过点C作CH⊥x轴于点H．

∵直线y＝x+1与x轴，y轴分别交于点A，B，

∴A（﹣1，0），B（0，1），

∴OA＝OB＝1，

∵OB∥CH，

∴＝＝1，

∴OA＝OH＝1，

∴CH＝2OB＝2，

∴C（1，2），

∵点C在y＝的图象上，

∴k＝2，

故答案为：2．

【点评】本题考查反比例函数与一次函数的交点，解题的关键是学会添加常用辅助线，利用三角形中位线定理解决问题．

13．（5分）如图，在Rt△ABC中，∠C＝90°，棱长为1的立方体的表面展开图有两条边分别在AC，BC上，有两个顶点在斜边AB上，则△ABC的面积为 　16　．

【分析】由题意得：△BDE、△EHF，△EGA是直角三角形，四边形DEGC是矩形，BC∥EG，DE∥HF∥AC，DE＝HF＝2，DC＝EG＝3，HE＝1，证明△EHF∽△EGA，得出＝，证明△BDE≌△EHF（ASA），得出DB＝HE＝1，求出AG＝6，再由三角形面积公式即可得出答案．

【解答】解：由题意得：△BDE、△EHF，△EGA是直角三角形，四边形DEGC是矩形，BC∥EG，DE∥HF∥AC，

DE＝HF＝2，DC＝EG＝3，HE＝1，

∴∠BDE＝∠EHF＝∠EGA＝90°，∠DEB＝∠HFE＝∠GAE，

∴△EHF∽△EGA，∴＝，

在△BDE和△EHF中，，

∴△BDE≌△EHF（ASA），

∴DB＝HE＝1，

∴＝，

∴AG＝6，

∴S△ABC＝S△BDE+S△EGA+S矩形DEGC＝×1×2+×3×6+2×3＝16，

故答案为：16．

【点评】本题考查了相似三角形的判定与性质、正方形的性质、直角三角形的性质、全等三角形的判定与性质等知识；证明三角形相似和三角形全等是解题的关键．

14．（5分）已知k为任意实数，随着k的变化，抛物线y＝x2﹣2（k﹣1）x+k2﹣3的顶点随之运动，则顶点运动时经过的路径与两条坐标轴围成图形的面积是 　1　．

【分析】将二次函数解析式化为顶点式可得抛物线顶点所在函数解析式，进而求解．

【解答】解：∵y＝x2﹣2（k﹣1）x+k2﹣3＝（x﹣k+1）2+2k﹣4，

∴抛物线顶点坐标为（k﹣1，2k﹣4），

设k﹣1＝x，则2k﹣4＝2x﹣2，

∴抛物线顶点在直线y＝2x﹣2上，

将x＝0代入y＝2x﹣2得y＝﹣2，

将y＝0代入y＝2x﹣2得0＝2x﹣2，

解得x＝1，

∴直线经过（0，﹣2），（1，0），

∴顶点运动时经过的路径与两条坐标轴围成图形的面积是S＝＝1，

故答案为：1．

【点评】本题考查二次函数的性质，解题关键是掌握二次函数图象与系数的关系，掌握求抛物线顶点轨迹的方法．

三、（本大题共2小题，每小题8分，满分16分）

15．（8分）已知某抛物线过点A（2，0），对称轴为x＝4，顶点在直线y＝x﹣1上，求此抛物线的解析式．

【分析】由于抛物线对称轴为直线x＝4，则顶点的横坐标为4，再利用顶点在直线y＝x﹣1上可确定抛物线的顶点坐标为（4，3），则可设顶点式y＝a（x﹣4）2+3，然后把A点坐标代入求出a即可．

【解答】解：∵当x＝4时，y＝x﹣1＝3，

∴抛物线的顶点坐标为（4，3），

设抛物线解析式为y＝a（x﹣4）2+3，

把A（2，0）代入得a×（2﹣4）2+3＝0，

解得a＝﹣，

∴抛物线解析式为y＝﹣（x﹣4）2+3．

【点评】本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．也考查了二次函数的性质．

16．（8分）如图，△ABC中，点E、F分别在边AB、AC上，∠1＝∠2．若BC＝4，AF＝2，CF＝3，求EF的长．

【分析】根据线段的和差可得AC的长，再根据相似三角形的判定与性质可得答案．

【解答】解：∵AF＝2，CF＝3，

∴AC＝5，

∵∠1＝∠2，∠A＝∠A，

∴△AEF∽△ABC，

∴AF：AC＝EF：BC，

即2：5＝EF：4，

∴EF＝．

【点评】此题考查的是相似三角形的判定与性质，掌握其性质定理是解决此题的关键．

四、（本大题共2小题，每小题8分，满分16分）

17．（8分）在如图的正方形格点纸中，每个小的四边形都是边长为1的正方形，A、B、C、D、F，H都是格点，AB与CD相交于O，AH与CD相交于E，求AO与BO的比值．

【分析】如图，由EH∥CF，利用平行线分线段成比例可求出EH＝，则AE＝，再证明△AOE∽△BOC，然后利用相似比可得到的值．

【解答】解：如图

∵EH∥CF，

∴，即＝，

∴EH＝，

∴AE＝AH﹣EH＝3﹣＝，

∵AE∥BC，

∴△AOE∽△BOC，

∴＝＝＝．

故AO与BO的比值为．

【点评】本题考查了相似三角形的判定与性质：三在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；灵活运用相似三角形的性质表示线段之间的关系．

18．（8分）在平面直角坐标系中，如果一个点的横坐标与纵坐标互为相反数，则称该点为“黎点”．例如（﹣1，1），（2022，﹣2022）都是“黎点”．

（1）求双曲线y＝上的“黎点”；

（2）若抛物线y＝ax2﹣7x+c（a、c为常数）上有且只有一个“黎点”，当a＞1时，求c的取值范围．

【分析】（1）设双曲线y＝上的“黎点”为（m，﹣m），构建方程求解即可；

（2）抛物线y＝ax2﹣7x+c（a、c为常数）上有且只有一个“黎点”，推出方程ax2﹣7x+c＝﹣x有且只有一个解，即ax2﹣6x+c＝0，Δ＝36﹣4ac＝0，可得结论．

【解答】解：（1）设双曲线y＝上的“黎点”为（m，﹣m），

则有﹣m＝，

∴m＝±3，

经检验，m＝±3的分式方程的解，

∴双曲线y＝上的“黎点”为（3，﹣3）或（﹣3，3）；

（2）∵抛物线y＝ax2﹣7x+c（a、c为常数）上有且只有一个“黎点”，

∴方程ax2﹣7x+c＝﹣x有且只有一个解，

即ax2﹣6x+c＝0，Δ＝36﹣4ac＝0，

∴ac＝9，

∴a＝，

∵a＞1，

∴0＜c＜9．

【点评】本题考查反比例函数图象上的点特征，二次函数的性质等知识，解题的关键是理解题意，学会用转化的思想思考问题．

五、（本大题共2小题，每小题10分，满分20分）

19．（10分）对于抛物线y＝x2﹣2x﹣3．

（1）它与x轴交点的坐标为 　（3，0）（﹣1，0）　，顶点坐标为 　（1，﹣4）　；

（2）在下面的坐标系中利用描点法画出此抛物线；

（3）利用以上信息解答下列问题：若关于x的一元二次方程x2﹣2x﹣3﹣t＝0（t为实数）在0＜x＜4的范围内有解，则t的取值范围是 　﹣4≤t＜5　.（直接写出结果）

【分析】（1）令y＝0，求出抛物线与x轴交点的坐标；

（2）如图所示，把表格中的值分别代入y＝x2﹣2x﹣3求出对应的数值；

（3）根据关于x的一元二次方程x2﹣2x﹣3﹣t＝0（t为实数）在0＜x＜4的范围内有解，得b2﹣4ac≥0，求出t取值范围，再把x＝0、x＝4分别代入x2﹣2x﹣3﹣t＝0，求出t的值，进而求出t的取值范围．

【解答】解：（1）令y＝0，0＝x2﹣2x﹣3．

解得，x1＝3，x2＝﹣1，

∴它与x轴交点的坐标为（3，0）（﹣1，0），

化为顶点式为：y＝（x﹣1）2﹣4

∴顶点为：（1，﹣4）；

故答案为：（3，0）（﹣1，0），（1，﹣4）；

（2）

（3）∵关于x的一元二次方程x2﹣2x﹣3﹣t＝0（t为实数）在0＜x＜4的范围内有解，

∴b2﹣4ac≥0，

∴4﹣4×1×（﹣3﹣t）≥0，

解得，t≥﹣4，

 把x＝0代入x2﹣2x﹣3﹣t＝0，

得t＝4，

把x＝4代入x2﹣2x﹣3﹣t＝0，

得t＝5，

∴t的取值范围是﹣4≤t＜5．

故答案为：﹣4≤t＜5．

【点评】本题考查二次函数的图象与性质，掌握二次函数的性质是解题关键．

20．（10分）如图，在等边三角形ABC中，D、E分别在AC、AB上，且，AE＝BE．

（1）求证△AED∽△CBD；

（2）已知△BDC的面积为，求BD长．

【分析】（1）（1）先根据等边三角形的性质得到∠A＝∠C＝60°，BC＝AB，由AE＝BE可得到CB＝2AE，再由，得到CD＝2AD，则＝，然后根据两边及其夹角法可得到结论；

（2）过F作FE∥BD交AC于E，根据平行线等分线段定理即可得到结论．

【解答】（1）证明：∵△ABC为正三角形，

∴∠A＝∠C＝60°，BC＝AB，

∵AE＝BE，

∴CB＝2AE，

∵，

∴CD＝2AD，

∴＝＝，

∵∠A＝∠C，

∴△AED∽△CBD；

（2）解：如图，过点D作DF⊥BC于点F，

设AD＝a，则AC＝3a，

∴CD＝2a，

∵△ABC是等边三角形，

∴BC＝AC＝3a，∠C＝60°，

∴CF＝a，DF＝CD＝a，

∴S△BDC＝•DF•BC＝••3a＝，

解得a＝4（负值舍去），

∴BC＝12，CF＝4，DF＝8，

∴BF＝8，

在Rt△BDF中，由勾股定理可知，BD＝4．

【点评】本题考查了相似三角形的判定和性质，含30°的直角三角形的三边关系，熟知相似三角形的判定定理是解题关键．

六、（本题满分12分）

21．（12分）如图，在平面直角坐标系xOy中，正方形ABCO的对角线BO在x轴上，若正方形ABCO的边长为2，点B在x轴负半轴上，反比例函数y＝的图象经过C点．

（1）求该反比例函数的解析式；

（2）当函数值y＞﹣2时，请直接写出自变量x的取值范围；

（3）若点P是反比例函数上的一点，且△PBO的面积恰好等于正方形ABCO的面积，求点P的坐标．

【分析】（1）求出C点的坐标，即可求出函数解析式；

（2）根据反比例函数的性质求出即可；

（3）根据面积求出P点的纵坐标，再代入函数解析式求出横坐标即可．

【解答】解：（1）

过C作CE⊥x轴于E，则∠CEB＝90°，

∵正方形ABCO的边长为2，

∴CO＝2，∠COE＝45°，

∴CE＝OE＝＝2，

即k＝﹣2×（﹣2）＝4，

所以反比例函数的解析式是y＝；

（2）把y＝﹣2代入y＝得：x＝﹣2，

所以当函数值y＞﹣2时，自变量x的取值范围是x＜﹣2或x＞0；

（3）设P点的纵坐标为a，

∵正方形ABCO的边长为2，

∴由勾股定理得：OB＝＝4，

∵△PBO的面积恰好等于正方形ABCO的面积，

∴×4×|a|＝2，

解得：a＝±4，

即P点的纵坐标是4或﹣4，

代入y＝得：x＝1或﹣1，

即P点的坐标是（1，4）或（﹣1，﹣4）．

【点评】本题考查了正方形的性质，用待定系数法求反比例函数的解析式和反比例函数的图象和性质，能熟记反比例函数的性质是解此题的关键．

七、（本题满分12分）

22．（12分）如图是甲、乙两人进行羽毛球练习赛时的一个瞬间，羽毛球飞行的高度y（m）与水平距离x（m）的路线为抛物线的一部分，如图，甲在O点正上方1m的P处发出一球，已知点O与球网的水平距离为5m，球网的高度为1.55m．羽毛球沿水平方向运动4m时，达到羽毛球距离地面最大高度是m．

（1）求羽毛球经过的路线对应的函数关系式；

（2）通过计算判断此球能否过网；

（3）若甲发球过网后，羽毛球飞行到离地面的高度为m的Q处时，乙扣球成功求此时乙与球网的水平距离．

【分析】（1）依题意，函数的顶点为（4，），则可设函数的解析式为：y＝a（x﹣4）2+，再由点（0，1）在抛物线上，代入求得a即可

（2）将x＝5代入（1）所求的函数解析式，求得y即可判断

（3）将y＝，代入函数解析式，求得x即可求乙与点O的距离，从而求得乙与球网的距离．

【解答】解：

（1）依题意，函数的顶点为（4，），

故设函数的解析式为：y＝a（x﹣4）2+，

∵点（0，1）在抛物线上

∴代入得1＝a（0﹣4）2+，解得a＝

则羽毛球经过的路线对应的函数关系式为：y＝﹣（x﹣4）2+

（2）由（1）知羽毛球经过的路线对应的函数关系式，

则当x＝5时，y＝×（5﹣4）2+＝＝1.625

∵1.625＞1.55

∴通过计算判断此球能过网

（3）当y＝时，

有＝（x﹣4）2+

解得x1＝1（舍去），x2＝7

则此时乙与球网的水平距离为：7﹣5＝2m

【点评】本题考查了二次函数的性质在实际生活中的应用．我们首先要吃透题意，确定变量，建立函数模型即可求解．

八、（本题满分14分）

23．（14分）如图，矩形ABCD中，点E在DC上，DE＝BE，AC与BD相交于点O，BE与AC相交于点F．

（1）若BE平分∠CBD，求证：BF⊥AC；

（2）找出图中与△OBF相似的三角形，并说明理由；

（3）若OF＝3，EF＝2，求DE的长度．

【分析】（1）根据矩形的性质和角平分线的定义，求得∠3＝∠6，从而求证BF⊥AC；

（2）根据相似三角形的判定进行分析判断；

（3）利用相似三角形的性质分析求解．

【解答】（1）证明：如图，

在矩形ABCD中，OD＝OC，AB∥CD，∠BCD＝90°，

∴∠2＝∠3＝∠4，∠3+∠5＝90°，

∵DE＝BE，

∴∠1＝∠2，

又∵BE平分∠DBC，

∴∠1＝∠6，

∴∠3＝∠6，

∴∠6+∠5＝90°，

∴BF⊥AC；

（2）解：与△OBF相似的三角形有△ECF，△BAF理由如下：

∵∠1＝∠3，∠EFC＝∠BFO，

∴△ECF∽△OBF，

∵DE＝BE，

∴∠1＝∠2，

又∵∠2＝∠4，

∴∠1＝∠4，

又∵∠BFA＝∠OFB，

∴△BAF∽△BOF；

（3）解：在矩形ABCD中，∠4＝∠3＝∠2，

∵∠1＝∠2，∴∠1＝∠4．

又∵∠OFB＝∠BFA，

∴△OBF∽△BFA．

∵∠1＝∠3，∠OFB＝∠EFC，

∴△OBF∽△ECF．

∴，

∴，即3CF＝2BF，

∴3（CF+OF）＝3CF+9＝2BF+9，

∴3OC＝2BF+9

∴3OA＝2BF+9①，

∵△ABF∽△BOF，

∴，

∴BF2＝OF•AF，

∴BF2＝3（OA+3）②，

联立①②，可得BF＝1±（负值舍去），

∴DE＝BE＝2+1+＝3+．

【点评】本题考查矩形的性质，相似三角形的判定和性质以及勾股定理，掌握相似三角形的判定和性质是解题关键．