2023年九年级中考数学复习：几何探究压轴题（面积问题）

这是一份2023年九年级中考数学复习：几何探究压轴题（面积问题），共13页。试卷主要包含了如图，矩形中，为等边三角形等内容，欢迎下载使用。
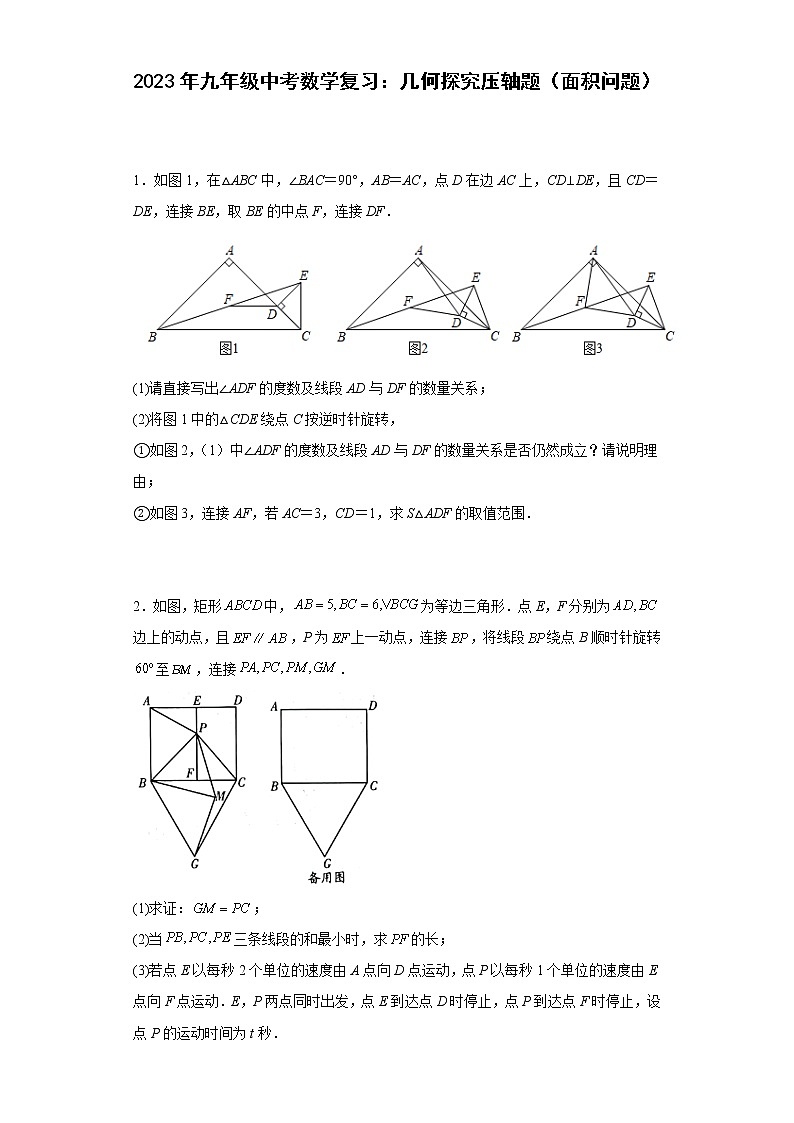
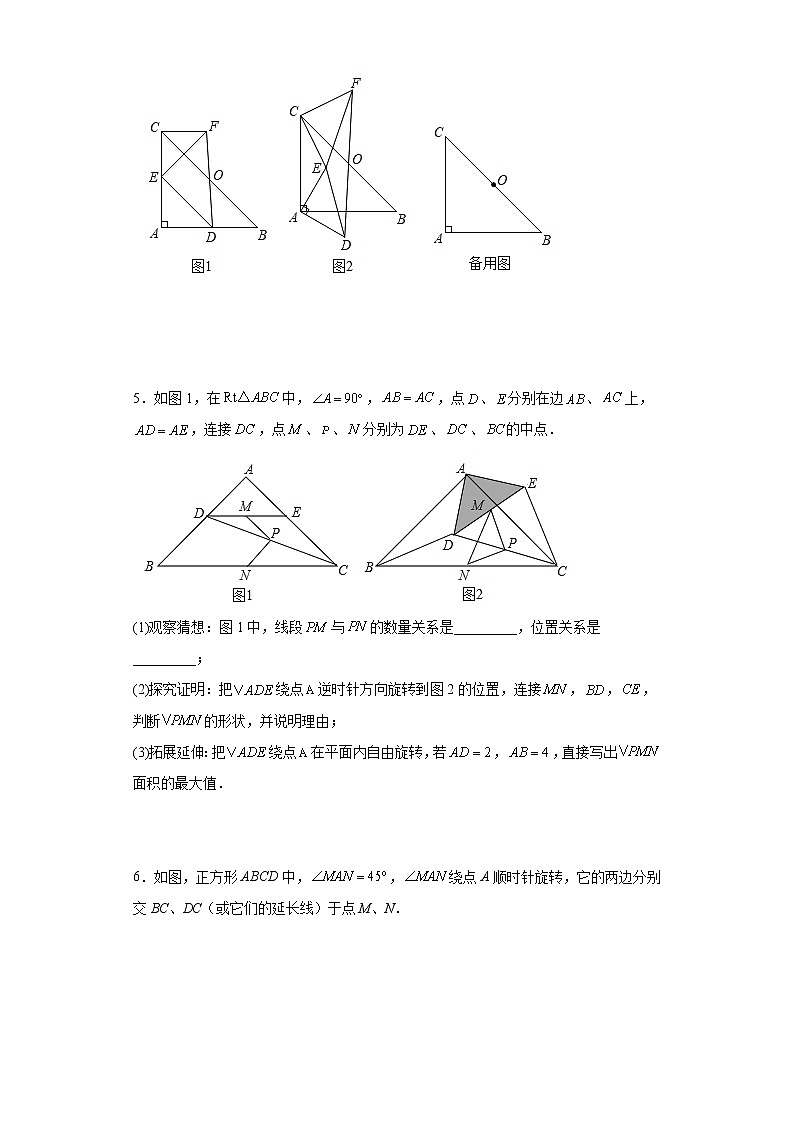
2023年九年级中考数学复习：几何探究压轴题（面积问题）  1．如图1，在△ABC中，∠BAC＝90°，AB＝AC，点D在边AC上，CD⊥DE，且CD＝DE，连接BE，取BE的中点F，连接DF．(1)请直接写出∠ADF的度数及线段AD与DF的数量关系；(2)将图1中的△CDE绕点C按逆时针旋转，①如图2，（1）中∠ADF的度数及线段AD与DF的数量关系是否仍然成立？请说明理由；②如图3，连接AF，若AC＝3，CD＝1，求S△ADF的取值范围．  2．如图，矩形中，为等边三角形．点E，F分别为边上的动点，且，P为上一动点，连接，将线段绕点B顺时针旋转至，连接．(1)求证：；(2)当三条线段的和最小时，求的长；(3)若点E以每秒2个单位的速度由A点向D点运动，点P以每秒1个单位的速度由E点向F点运动．E，P两点同时出发，点E到达点D时停止，点P到达点F时停止，设点P的运动时间为t秒．①求t为何值时，与相似；②求的面积S的最小值．   3．在△ABC中，AB＝AC，∠BAC＝90°，D为平面内的一点．（1）如图1，当点D在边BC上时，BD＝2，且∠BAD＝30°，AD＝　 　；（2）如图2，当点D在△ABC的外部，且满足∠BDC﹣∠ADC＝45°，求证：BD＝AD；（3）如图3，若AB＝4，当D、E分别为AB、AC的中点，把△DAE绕A点顺时针旋转，设旋转角为α（0＜α≤180°）直线BD与CE的交点为P，连接PA，直接出△PAB面积的最大值 　 　．    4．如图1，△ABC为等腰直角三角形，∠BAC＝90°，AB＝AC，点D在AB边上，点E在AC边上，AD＝AE，连接DE，取BC边的中点O，连接DO并延长到点F，使OF＝OD，连接CF．（1）请判断△CEF的形状，并说明理由；（2）将（1）中△ADE绕点A旋转，连接CE，（1）中的结论是否仍然成立，若成立，请仅就图2所示情况给出证明，若不成立，请说明理由；（3）若AB＝6，AD＝4，将△ADE由图1位置绕点A旋转，当点B，E，D三点共线时，请直接写出△CEF的面积．   5．如图1，在中，，，点、分别在边、上，，连接，点、、分别为、、的中点．(1)观察猜想：图1中，线段与的数量关系是_________，位置关系是_________；(2)探究证明：把绕点逆时针方向旋转到图2的位置，连接，，，判断的形状，并说明理由；(3)拓展延伸：把绕点在平面内自由旋转，若，，直接写出面积的最大值．  6．如图，正方形ABCD中，，绕点A顺时针旋转，它的两边分别交BC、DC（或它们的延长线）于点M、N．(1)如图1，求证：；(2)当，时，求的面积；(3)当绕点A旋转到如图2位置时，线段BM、DN和MN之间有怎样的数量关系？请写出你的猜想并证明．   7．如图1，在中，，点D是边上的一点，且，过点D做边的垂线，交边于点E，将绕点B顺时针方向旋转，记旋转角为．(1)【问题发现】当时，的值为________，直线相交形成的较小角的度数为________；(2)【拓展探究】试判断：在旋转过程中，（1）中的两个结论有无变化？请仅就图2的情况给出证明；(3)【问题解决】当旋转至A，D，E三点在同一条直线上时，请直接写出的面积．  8．已知Rt△ABC中，AC＝BC，∠C＝90°，D为AB边的中点，∠EDF＝90°，∠EDF绕D点旋转，它的两边分别交AC、CB（或它们的延长线）于E、F．(1)如图1，当∠EDF绕D点旋转到DE⊥AC于E时，易证S△DEF＋S△CEF与S△ABC的数量关系为__________；(2)如图2，当∠EDF绕D点旋转到DE和AC不垂直时，上述结论是否成立？若成立，请给予证明；(3)如图3，这种情况下，请猜想S△DEF、S△CEF、S△ABC的数量关系，不需证明．    9．在△ABC中，CA＝CB，∠ACB＝a，将△CAD绕点C按逆时针方向旋转角a得到△CBE，点A，D的对应点分别为点B，E．(1)如图1，若A，D，E三点在同一直线上，则∠CDE=　    （用含a的代数式表示）；(2)如图2，若A，D，E三点在同一直线上，a=60°，过点C作CF⊥AE于点F，然后探究线段CF，AE，BE之间的数量关系，并证明你的结论；(3)图3中，若CA＝2，CD＝2，将△DCE绕点C旋转，当       时，△CAD的面积最大，最大面积是     ．     10．如图，在中，，，点D是外一动点，连接，把AD绕点A逆时针旋转90°，得到，连接，，与交于点F，且．（1）如图1，若，求的长；（2）如图2，若点H、G分别为线段、的中点，连接，求证：；（3）如图3，在（2）的条件下，若，将绕点F顺时针旋转角，得到，连接，取中点Q，连接，当线段最小时，请直接写出的面积．  11．如图1，△ABC和△DEC均为等腰三角形，且∠ACB=∠DCE=90°，连接BE，AD，两条线段所在的直线交于点P.（1）线段BE与AD有何数量关系和位置关系，请说明理由．（2）若已知BC=12，DC=5，△DEC绕点C顺时针旋转，①如图2，当点D恰好落在BC的延长线上时，求AP的长；②在旋转一周的过程中，设△PAB的面积为S，求S的最值．   12．直角三角板ABC中，∠A=30°，BC＝1．将其绕直角顶点C逆时针旋转一个角（且），得到Rt△．(1)如图，当边经过点B时，求旋转角的度数；(2)在三角板旋转的过程中，边与AB所在直线交于点D，过点 D作DE∥交边于点E，连接BE．①当时，设AD=，BE=，求与之间的函数解析式及自变量 的取值范围；②当时，求AD的长．   13．在中中．，，点E在射线CB上运动．连接AE，将线段AE绕点E顺时针旋转90°得到EF，连接CF．(1)如图1，点E在点B的左侧运动；①当，时，则_________°；②猜想线段CA，CF与CE之间的数量关系为_________．(2)如图2，点E在线段CB上运动时，第（1）间中线段CA，CF与CE之间的数量关系是否仍然成立如果成立，请说明理由；如果不成立，请求出它们之间新的数量关系．(3)点E在射线CB上运动，，设，以A，E，C，F为顶点的四边形面积为y，请直接写出y与x之间的函数关系式（不用写出x的取值范围）．   14．（1）如图1，在等腰直角三角形ABC中，∠C＝90°，点O为AB的中点，点M为AC上一点，将射线OM绕点O顺时针旋转90°交BC于点N，则OM与ON的数量关系为 　　；（2）如图2，在等腰三角形ABC中，∠C＝120°，点O为AB的中点，点M为AC上一点，将射线OM绕点O顺时针旋转60°交BC于点N，则OM与ON的数量关系是否改变，请说明理由；（3）如图3，点O为正方形ABCD对角线的交点，点P为DO的中点，点M为直线BC上一点，将射线OM绕点O顺时针旋转90°交直线AB于点N，若AB＝4，当△PMN的面积为时，直接写出线段BN的长．  15．定义：两个顶角相等且顶角顶点重合的等腰三角形组合称为“相似等腰组”．如图1，等腰△ABC和等腰△ADE即为“相似等腰组”．(1)如图2，将上述“相似等腰组”中的△ADE统看点A逆时针旋转一定角度，判断△ABD和△ACE是否全等，并说明理由；(2)如图3，等腰△ABC和等腰△ADE是“相似等腰组”，且∠BAC＝90°，DC和BE相交于点O，判断DC和BE的位置及大小关系，并说明理由；(3)如图4，在等边△ABC中，D是△ABC内部一点，且，，，直接写出△ABC的面积．   16．如图，在等腰和等腰中，． (1)观察猜想：如图1，点在上，线段与的关系是_________；(2)探究证明：把绕直角顶点旋转到图2的位置，（1）中的结论还成立吗？说明理由；(3)拓展延伸：把绕点在平面内转动一周，若，，、交于点时，连接，直接写出最大面积_________．   17．如图1，在Rt△ABC中，∠A=90°，AB=AC，点D，E分别在边AB，AC上，AD=AE，连接DC，点M，P，N分别为DE，DC，BC的中点．(1)观察猜想：图1中，请判断线段PM与PN的数量关系和位置关系，并说明理由；(2)探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；(3)拓展延伸：把△ADE绕点A在平面内自由旋转，若AD=3，AB=7，请直接写出△PMN面积的最大值．   18．如图1，在等腰三角形ABC中，∠A＝120°，AB＝AC，点D、E分别在边AB、AC上，AD＝AE，连接BE，点M、N、P分别为DE、BE、BC的中点．(1)观察猜想：图1中，线段NM、NP的数量关系是        ，∠MNP的大小为        ；(2)探究证明：把△ADE绕点A顺时针方向旋转到如图2所示的位置，连接MP、BD、CE，判断△MNP的形状，并说明理由；(3)拓展延伸：当∠BAC＝90°，AB＝AC＝10，AD＝AE＝6时，把△ADE绕点A在平面内自由旋转，如图3，请求出△MNP面积的最大值．
参考答案：1．(1)∠ADF=45°，AD=DF；(2)①成立，②1≤S△ADF≤4. 2． (2)(3)①；② 3．（1）；（3）4．（1） △CEF是等腰直角三角形，；（2）成立；（3）或．5．(1)，(2)是等腰直角三角形， (3) 6． (2)6(3)  7．(1)，；(2)无变化 (3)或． 8．(1)S△DEF＋S△CEF＝S△ABC(2)上述结论S△DEF＋S△CEF＝S△ABC成立 (3)S△DEF－S△CEF＝S△ABC 9．(1)(2)AE=BE+CF； (3)CD⊥AC；210．（1）；（3）．11．（1）BE=AD，BE与AD互相垂直，证明详见解析；（2）①AP=；②最小47，最大7212．(1)＝；(2)① （0﹤﹤2）；②AD=1或． 13．(1)①30；②AC+CF=CE；(2)CA-CF=CE；(3)当点E在点B左侧运动时，y=；当点E在点B右侧运动时，y=． 14．（1）；（2），见解析；（3）15．(1)全等； (2)；(3)  16．(1)，；(2)结论仍成立， (3)． 17．(1)PM=PN，PM⊥PN． (2)△PMN是等腰直角三角形． (3)S△PMN最大= 18．(1)MN＝NP，∠MNP＝60°；(2)△MNP是等边三角形， (3)△MNP面积的最大值是32．