压轴题20以相似为背景的几何类比探究压轴问题-2023年中考数学压轴题专项训练（全国通用）

2023年中考数学压轴题专项训练

压轴题20以相似为背景的几何类比探究压轴问题

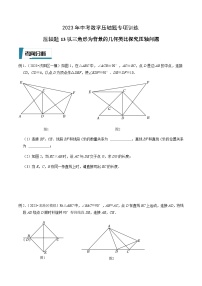
例1．（2023•青山区模拟）（1）已知，直线AC与BD交于点O．

①如图1，若∠A＝∠D，求证：AO•CO＝BO•DO；

②如图2，若∠A+∠D＝180°，求证：；

（2）如图3，在△ABC中，∠A＝60°，E为BD中点，且∠BEC＝120°，DE：CD＝1：n．则AB：CE＝　      　．

​

例2．（2023•慈溪市一模）【证明体验】（1）如图1，在△ABC中，D为AB边上一点，连结CD，若∠ACD＝∠ABC，求证：AC2＝AD•AB．

（2）在Rt△ABC中，∠ACB＝90°，∠ABC＝60°，BC＝2，D为AB边上一动点，连结CD，E为CD中点，连结BE．

【思考探究】①如图2，当∠ACD＝∠DBE时，求AD的长．

【拓展延伸】②如图3，当∠DEB＝30°时，求AD的长．

例3．（2023•温江区校级模拟）如图1，矩形ABCD中，∠ACB＝30°，点E在对角线AC上，点F在边AD上运动，连接EF，作∠FEG＝90°，交直线BC于点G，且，AB＝6．

（1）如图2，当点F与点D重合时，求的值；

（2）点F在边AD上运动过程中，当△AEF成为以AE为腰的等腰三角形时，求BG的长；

（3）记点F关于直线AC的轴对称点为点P，若点P落在∠EBC的内部（不含边界），求DF的取值范围．

例4．（2023•广水市模拟）爱动脑筋的小明同学在学习完角平分线的性质一节后意犹未尽经过思考发现里面还有一个有趣的结论：

（1）【问题发现】如图1所示，若AD是∠BAC的角平分线，可得到结论：．

小明的解法如下：

过点D作DE⊥AB于点E，DF⊥AC于点F，过点A作AG⊥BC于点G，

∵AD是∠BAC的角平分线，且DE⊥AB，DF⊥AC，

∴　        　，

，

∵，

∴．

（2）【类比探究】如图2所示，若AD是∠BAC的外角平分线，AD与BC的延长线交于点D．求证：；

（3）【直接应用】如图3所示，Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于D，若BD＝10，CD＝6，在不添加辅助线的情况下直接写出AB＝　     　．

（4）【拓展应用】如图4所示，在△ABC中，∠ABC＝90°，AB＝6，BC＝8，将△ABC先沿∠BAC的平分线AD折叠，B点刚好落在AC上的E点，剪掉重叠部分（即四边形ABDE），再将余下部分（△CDE）沿∠DEC的平分线EF折叠，再剪掉重叠部分（即四边形DEGF），求出剩余部分△FCG的面积．

1．（2023•仪征市一模）已知菱形ABCD中，点E是对角线AC上一点，点F是边AD上一点，连接EF、BE、CF．

【特例探究】：（1）如图1，若∠ABC＝60°且EF∥CD，线段BE、CF满足的数量关系是 　        　；

（2）如图2，若∠ABC＝90°且EF⊥AC，判定线段BE、CF满足的数量关系，并说明理由；

【一般探究】（3）如图3，根据特例的探究，若∠BAC＝α，AE＝EF，请求出的值（用含α的式子表示）；

【发现应用】（4）如图3，根据“一般探究”中的条件，若菱形边长为1，，点F在直线AD上运动，则△CEF面积的最大值为 　                  　．

2．（2023•浦东新区二模）已知：如图，在梯形ABCD中，AD∥BC，过点B作BE⊥AD，垂足为点E，点G在边AD上，连接BG、CG，对角线AC与BE、BG分别交于点F、H，且AE•BG＝AF•BE．

（1）求证：BG⊥AC；

（2）如果∠DGC＝2∠DCG，且DC是DG与DA的比例中项，求证：四边形ABCG是菱形．

3．（2023•周村区一模）如图，在正方形ABCD中，E是边BC上的一点，过点E作BD的垂线交BD于点P，交AB于点F，连接AP并延长交BC于点G．

（1）求证：PE＝PF；

（2）若BG＝CE，求∠EPG的度数；

（3）若AB＝6，EG＝1，求△PGE的面积．

4．（2023•市北区一模）如图所示，矩形ABCD，AB＝3cm，BC＝5cm，E为边AD上一点，ED＝1cm．点P从点B出发，沿BE方向匀速运动，速度为1cm/s；同时，点Q从点C出发，沿CB方向匀速运动，速度为1cm/s．设运动时间为t（s）（0＜t＜5）．解答下列问题：

（1）当t为何值时，以P、Q、B为顶点的三角形和△ABE相似；

（2）设五边形PEDCQ的面积为S（cm2），求S与t之间的函数关系式；

（3）连接CE，取CE中点F，连接DF，在运动过程中，是否存在某一时刻t，使PQ∥DF？若存在，请直接给出t的值（不必提供求解过程）；若不存在，请说明理由．

​

5．（2023•历下区一模）如图1，已知正方形AFEG与正方形ABCD有公共顶点A，点E在正方形ABCD的对角线AC上（AG＜AD）．

（1）如图2，正方形AFEG绕A点顺时针方向旋转α（0°＜α＜90°），DG和BF的数量关系是 　        　，位置关系是 　        　；

（2）如图3，正方形AFEG绕A点逆时针方向旋转α（0°＜α＜90°），求的值以及直线CE和直线DG所夹锐角的度数；

（3）如图4，AB＝8，点N在对角线AC上，CN，将正方形AFEG绕A顺时针方向旋转α（0°＜α＜360°），点M是边CD的中点，过点M作MH∥DG交EC于点H；在旋转过程中，线段NH的长度是否变化？如果不变，请直接写出NH的长度；如果改变，请说明理由．

6．（2023•碑林区校级三模）数学探究小组利用一些三角形彩纸裁剪面积最大的内接正方形，他们就有关问题进行了探究：

定义：如果一个正方形的四个顶点都在一个三角形的边上，那么我们就把这个正方形叫做三角形的内接正方形．

作图：如图1，正方形DEFG的顶点E，F在边AB上，顶点D在边AC上，在△ABC及其内部，以A为位似中心，作正方形DEFG的位似正方形D′E′F′G′，且使正方形D′E′F′G′的面积最大．

实践操作：

（1）第一小组拿到的钝角三角形原材料，你认为在钝角三角形中存在 　   　个内接正方形；

（2）第二小组拿到的是直角三角形原材料，小明说：在直角三角形中，两个顶点都在斜边上的内接正方形的面积较大．小丽同学认为他的结论不正确，她通过计算腰长为1的等腰直角三角形（如图2和图3）的情况给予说明，请你帮助小丽同学完成计算和说理过程；

（3）第三小组拿到的是不等边锐角三角形原材料，小华同学认为：在不等边锐角三角形中，两个顶点都在较大边上的内接正方形的面积反而较小．小华同学已经写出了题设条件，请你帮助他完成推理过程．如图4，设锐角△ABC的三条边分别为a、b、c不妨设a＞b＞c，三条边上的对应高分别为ha、hb、hc，内接正方形的边长分别为xa、xb、xc．

7．（2023•宁波一模）【基础巩固】

（1）如图1，AB⊥BC于点B，CE⊥BC于点C，AC⊥DE交BC于点D，求证：．

【尝试应用】

（2）如图2，在矩形ABCD中，E是BC上的一点，作DF⊥AE交BC于点F，CE＝EF，若AB＝2，AD＝4，求的值．

【拓展提高】

（3）如图3，菱形ABCD的边长为为AD上的一点，作DG⊥CE交AC于点F，交AB于点G，且CE＝2DF，求BG的长．

8．（2023•西湖区模拟）如图，在△ABC中，点D、E、F分别在AB、BC、AC上，且DF∥BC，EF∥AB．

（1）求证：△FEC∽△ADF；

（2）设CFAC．

①若EF＝3，求线段AB的长；

②若S△FEC＝1，求S△ADF的值．

9．（2023•西湖区模拟）如图，在菱形ABCD中，AB＝2，∠ABC＝60°，E，F分别是线段AB和AB的延长线上的一点，且BF＝BE，连接CE，DF交于点G，连接BG．设k（k＞0）．

（1）当k＝1时，求CE的长；

（2）在（1）的条件下，求BG的长；

（3）求△DCG的面积（用含k的代数式表示）．

10．（2023•包河区一模）如图1，AB＝AC＝2CD，DC∥AB，将△ACD绕点C逆时针旋转得到△FCE，使点D落在AC的点E处，AB与CF相交于点O，AB与EF相交于点G，连接BF．

（1）求证：△ABE≌△CAD；

（2）求证：AC∥FB；

（3）若点D，E，F在同一条直线上，如图2，求的值．（温馨提示：请用简洁的方式表示角）

11．（2023•沭阳县一模）我们定义：三角形中，如果有一个角是另一个角的2倍，那么称这个三角形是2倍角三角形．

（1）定义应用：如果一个等腰三角形是2倍角三角形，则其底角的度数为 　          　；

（2）性质探索：小思同学通过对2倍角三角形的研究，发现：在△ABC中，如果∠A＝2∠B＝90°，那么BC2＝AC（AB+AC），下面是小思同学的证明方法：已知：如图1，在△ABC中，∠A＝90°，∠B＝45°．求证：BC2＝AC（AB+AC）．证明：如图1，延长CA到D，使得AD＝AB，连接BD，∴∠D＝∠ABD，AB+AC＝AD+AC＝CD；∵∠CAB＝∠D+∠ABD＝2∠D，∠CAB＝90°∴∠D＝45°，∵∠ABC＝45°，∴∠D＝∠ABC，又∠C＝∠C∴△ABC∽△BCD，∴∴BC2＝AC•CD∴BC2＝AC（AB+AC）

根据上述材料提供的信息，请你完成下列情形的证明：

已知：如图2，在△ABC中，∠A＝2∠B，求证：BC2＝AC（AB+AC）；

（3）性质应用：已知：如图3，在△ABC中，∠C＝2∠B，AB＝6，BC＝5，则AC＝　   　；

（4）拓展应用：已知：如图4，在△ABC中，∠ABC＝3∠A，AC＝5，BC＝3，求AB的长．

12．（2023•庐阳区校级一模）已知：如图1，在Rt△ABC中，∠ACB＝90°，CD是∠ACB的平分线，连接DA、DB，且DA⊥DB于点D．

（1）求证：DA＝DB；

（2）如图2，点E、F分别是边CD、AC上的点，且BE⊥EF于点E，求的值．

13．（2023•武侯区校级模拟）如图，在矩形ABCD中，AB＝kBC （0＜k＜1 ），将线段AB绕点A逆时针旋转α度（0＜α＜90 ）得到线段AE，过点E作AE的垂线交射线CD于点H，交射线AD于点M．

[尝试初探]

（1）当点M在AD延长线上运动时，∠BAE与∠AME始终相等，且△AEM与△HDM始终相似，请说明理由；

[深入探究]

（2）若k，随着线段AE的旋转，点H的位置也随之发生变化，当CHCD时，求tanα的值；

[拓展延伸]

（3）连接ED，当△EDM为等腰三角形时，求tanα的值（用含k的代数式表示）．

14．（2023•汶上县一模）【问题呈现】

（1）如图1，△ABC和△ADE都是等边三角形，连接BD，CE，求证：BD＝CE；

【类比探究】

（2）如图2，△ABC和△ADE都是等腰直角三角形，∠ABC＝∠ADE＝90°，连接BD，CE，求的值；

【拓展提升】

（3）如图3，△ABC和△ADE都是直角三角形，∠ABC＝∠ADE＝90°，且，连接BD，CE，直接写出的值．

15．（2023•宜兴市一模）如图，矩形ABCD中，AB＝5，BC＝4．点P在AD上运动（点P不与点A、D重合）将△ABP沿直线翻折，使得点A落在矩形内的点M处（包括矩形边界）．

（1）求AP的取值范围；

（2）连接DM并延长交矩形ABCD的AB边于点G，当∠ABM＝2∠ADG时，求AP的长．

16．（2023•汉阳区校级模拟）【问题背景】

（1）如图1，在△ABC中，D为AB上一点，∠ACD＝∠B．求证：AC2＝AD•AB．

【尝试应用】

（2）如图2，在平行四边形ABCD中，E为BC上一点，F为CD延长线上一点，FE、FB分别交AD于点H、G．∠BFE＝∠A，若BF＝8，BE＝6，GH：AG＝9：8，求FD：DC的值．

【拓展创新】

（3）如图3，在菱形ABCD中，E是AB上一点，F是△ABC内一点，EF∥AC，AC＝2EF，若∠EDF∠BAD，AE＝4，DF＝10，直接写出菱形ABCD的边长为 　                 　．

17．（2023•来安县一模）已知△ABC和△ADE有公共的顶点A，AB＝AC，AD＝AE，且∠BAC＝∠DAE．AC与DE相交于点G，连接BE，CD．

（1）若点B，E，D在一条直线上，如图1，求证：∠BAC＝∠BDC；

（2）将△ADE绕点A逆时针方向旋转一定的角度，DE的延长线交BC于点F，如图2

①证明：AE•CG＝DG•CF；

②若∠AEB＝∠BAC＝90°，求的值．

18．（2023•鄞州区校级一模）（1）特殊发现

如图1，正方形BEFG与正方形ABCD的顶点B重合，BE、BG分别在BC、BA边上，连接DF，则有：

①　             　；   ②直线DF与直线AG所夹的锐角等于 　     　度；

（2）理解运用

将图1中的正方形BEFG绕点B逆时针旋转，连接DF、AG，

①如图2，（1）中的结论是否仍然成立？请说明理由；

②如图3，若D、F、G三点在同一直线上，且过AB边的中点O，BE＝4，直接写出AB的长 　              　；

（3）拓展延伸

如图4，点P是正方形ABCD的AB边上一动点（不与A、B重合），连接PC，沿PC将△PBC翻折到△PEC位置，连接DE并延长，与CP的延长线交于点F，连接AF，若AB＝4PB，则的值是否是定值？请说明理由．

19．（2023•江西模拟）【课本再现】黄金分割是一种最能引起美感的分割比例，具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值．我们知道：如图1，如果，那么称点C为线段AB的黄金分割点．

（1）【问题发现】如图1，请直接写出CB与AC的比值是 　                  　；

（2）【尺规作黄金分割点】如图2，在Rt△ABC中，∠C＝90°，BC＝1，AC＝2，则AB＝　             　，在BA上截取BD＝BC，则AD＝　               　，在AC上截取AE＝AD，则的值为 　                  　；

（3）【问题解决】如图3，用边长为4的正方形纸片进行如下操作：对折正方形ABDE得折痕MN，连接EN，点A对应点H，得折痕CE，试说明：C是AB的黄金分割点；

（4）【拓展延伸】如图4，正方形ABCD中，M为对角线BD上一点，点N在边CD上，且CN＜DN，当N为CD的黄金分割点时，∠AMB＝∠ANB，连NM，延长NM交AD于E，请用相似的知识求出AE：DE的值为 　                  　．

20．（2023•庐阳区校级一模）【初步尝试】

（1）如图1，在正方形ABCD中，点E，F分别为AB、AD边上的点且DE⊥CF，求证：DE＝CF．

（2）【思考探究】

如图2，在矩形ABCD中，AB＝3，BC＝2，点E为BC中点，点F为AE上一点，连接CF、DF且CF＝CD，求DF的值．

（3）【拓展应用】

如图3，在四边形ABCD中，∠DAB＝90°，∠ABC＝45°，，点E、F分别在线段AB、AD上，且CE⊥BF．直接写出的值．