2023年九年级中考数学复习：几何探究压轴题（角度问题）

2023年九年级中考数学复习：几何探究压轴题（角度问题）

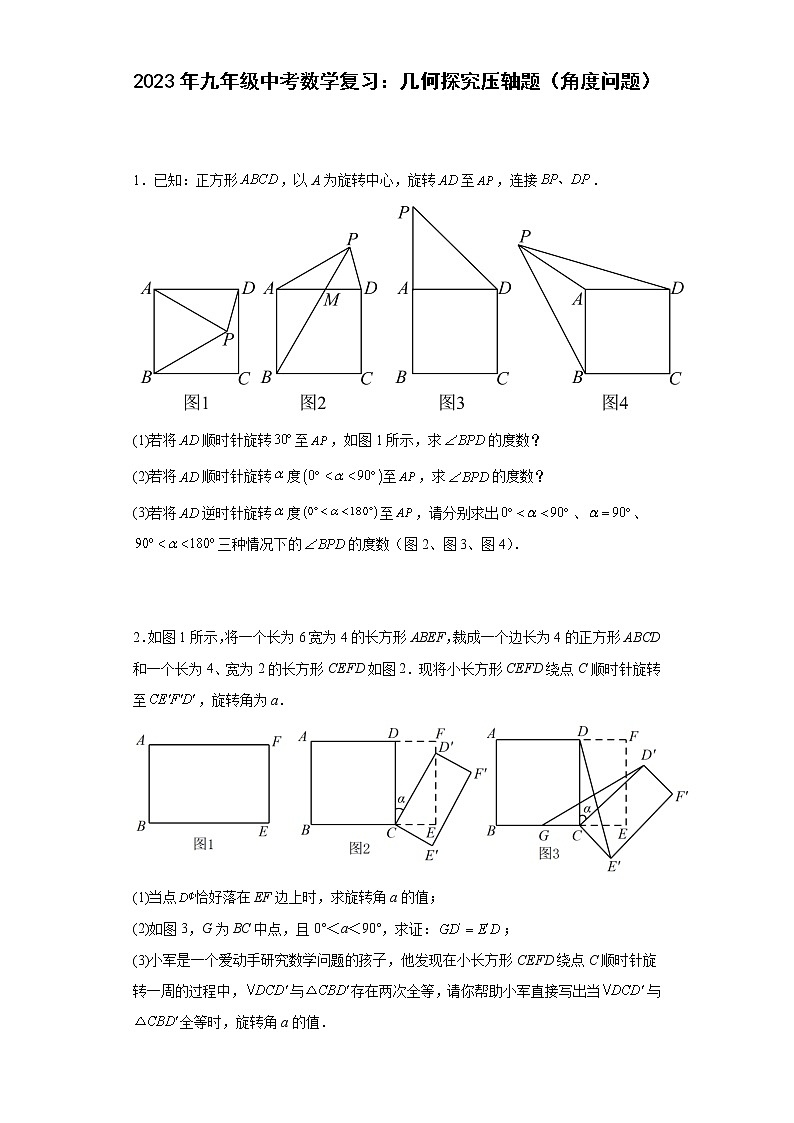
1．已知：正方形，以A为旋转中心，旋转至，连接．

(1)若将顺时针旋转至，如图1所示，求的度数？

(2)若将顺时针旋转度至，求的度数？

(3)若将逆时针旋转度至，请分别求出、、三种情况下的的度数（图2、图3、图4）．

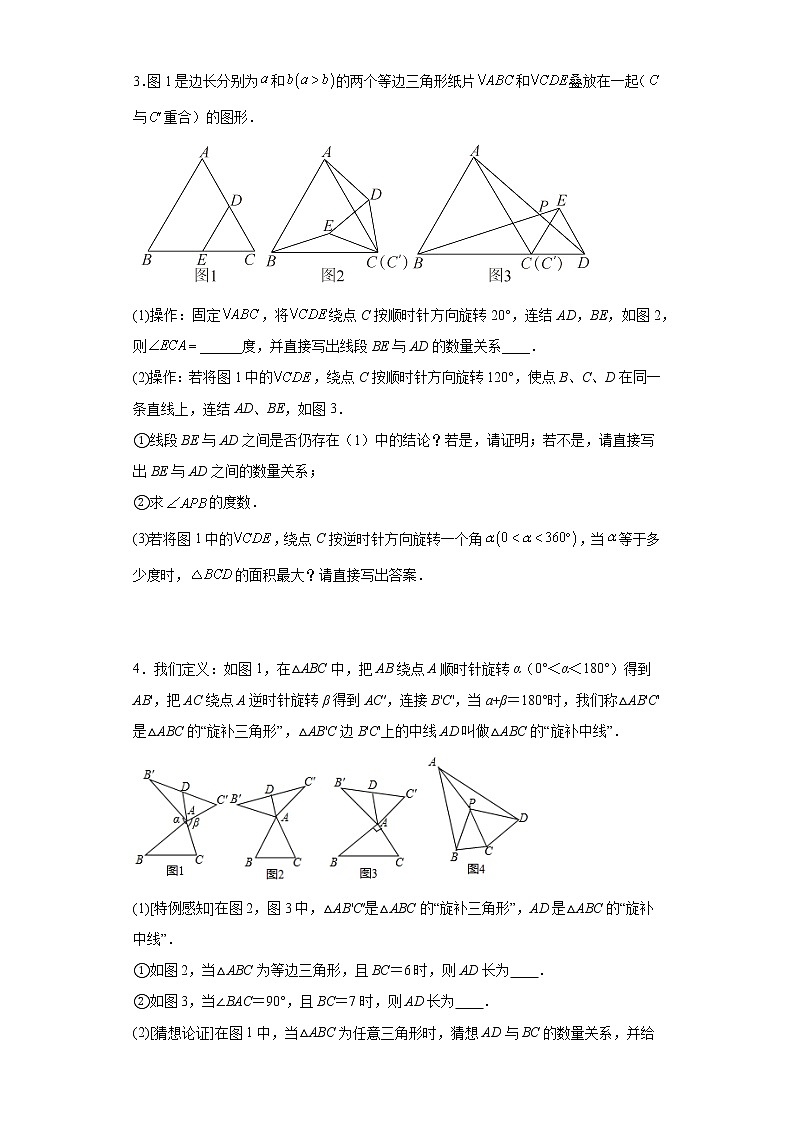
2．如图1所示，将一个长为6宽为4的长方形ABEF，裁成一个边长为4的正方形ABCD和一个长为4、宽为2的长方形CEFD如图2．现将小长方形CEFD绕点C顺时针旋转至，旋转角为a．

(1)当点恰好落在EF边上时，求旋转角a的值；

(2)如图3，G为BC中点，且0°＜a＜90°，求证：；

(3)小军是一个爱动手研究数学问题的孩子，他发现在小长方形CEFD绕点C顺时针旋转一周的过程中，与存在两次全等，请你帮助小军直接写出当与全等时，旋转角a的值．

3．图1是边长分别为和的两个等边三角形纸片和叠放在一起（与重合）的图形．

(1)操作：固定，将绕点C按顺时针方向旋转20°，连结AD，BE，如图2，则______度，并直接写出线段BE与AD的数量关系____．

(2)操作：若将图1中的，绕点C按顺时针方向旋转120°，使点B、C、D在同一条直线上，连结AD、BE，如图3．

①线段BE与AD之间是否仍存在（1）中的结论？若是，请证明；若不是，请直接写出BE与AD之间的数量关系；

②求的度数．

(3)若将图1中的，绕点C按逆时针方向旋转一个角，当等于多少度时，的面积最大？请直接写出答案．

4．我们定义：如图1，在△ABC中，把AB绕点A顺时针旋转α（0°＜α＜180°）得到AB'，把AC绕点A逆时针旋转β得到AC′，连接B'C'，当a+β＝180°时，我们称△AB'C'是△ABC的“旋补三角形”，△AB'C边B'C'上的中线AD叫做△ABC的“旋补中线”．

(1)[特例感知]在图2，图3中，△AB'C′是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．

①如图2，当△ABC为等边三角形，且BC＝6时，则AD长为　　．

②如图3，当∠BAC＝90°，且BC＝7时，则AD长为　　．

(2)[猜想论证]在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．（如果你没有找到证明思路，可以考虑延长AD或延长B'A，…）

(3)[拓展应用]如图4，在四边形ABCD中，∠BCD＝150°，AB＝12，CD＝6，以CD为边在四边形ABCD内部作等边△PCD，连接AP，BP．若△PAD是△PBC的“旋补三角形”，请直接写出△PBC的“旋补中线”长及四边形ABCD的边AD长．

5．如图，已知正方形ABCD，点E为AB上的一点，，交BD于点F．

(1)如图1，直按写出的值_______；

(2)将△EBF绕点B顺时针旋转到如图2所示的位置，连接AE、DF，猜想DF与AE的数量关系，并证明你的结论；

(3)如图3，当BE=BA时，其他条件不变，△EBF绕点B顺时针旋转，设旋转角为，当为何值时EA=ED?请在图3或备用图中画出图形并求出的值．

6．如图，已知正方形ABCD，将AD绕点A逆时针方向旋转到AP的位置，分别过点作，垂足分别为点、．

(1)求证：；

(2)联结，如果，求的正切值；

(3)联结，如果，求的值．

7．把两个等腰直角△ABC和△ADE按如图1所示的位置摆放，将△ADE绕点A按逆时针方向旋转，如图2，连接BD，EC，设旋转角α（0°＜α＜360°）．

（Ⅰ）当DE⊥AC时，旋转角α＝　 　度，AD与BC的位置关系是 　 　，AE与BC的位置关系是 　 　；

（Ⅱ）当点D在线段BE上时，求∠BEC的度数；

（Ⅲ）当旋转角α＝　 　时，△ABD的面积最大．

8．已知：在中，，，将绕点顺时针旋转一定的角度得到，点、的对应点分别是、．

（1）如图1，若时，连接，求证：；

（2）如图2，当点恰好在上时，求的度数；

（3）如图3，点、的坐标分别是，，点是线段上的一个动点，点是线段上的一个动点，是否存在这样的点、使得为等腰三角形且为直角三角形？若存在，请求出满足条件的点的坐标；若不存在，请说明理由．

9．把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中，将它绕点C顺时针旋转a角，旋转后的矩形记为矩形EDCF．在旋转过程中，

（1）如图①，当点E在射线CB上时，E点坐标为     ；

（2）当△CBD是等边三角形时，旋转角a的度数是     （a为锐角时）；

（3）如图②，设EF与BC交于点G，当EG=CG时，求点G的坐标；

（4）如图③，当旋转角a=90°时，请判断矩形EDCF的对称中心H是否在以C为顶点，且经过点A的抛物线上．

10．如图，是等边三角形，点D是边的中点，以D为顶点作一个的角，角的两边分别交直线于M、N两点，以点D为中心旋转（的度数不变）

(1)如图①，若，求证：；

(2)如图②，若与不垂直，且点M在边上，点N在边上时，（1）中的结论是否成立？并说明理由；

(3)如图③，若与不垂直，且点M在边上，点N在边的延长线上时，（1）中的结论是否成立？若不成立，写出之间的数量关系，并说明理由．

11．如图1，在中，，点为边上的一点， 将绕点逆时针旋转 得到，易得，连接．

(1)求的度数．

(2)当时，求的长．

(3)如图2，在(2)的条件下，取中点，连接交于，试探究线段的数量关系和位置关系，并说明理由．

12．如图①，和是有公共顶点的等腰直角三角形，，点P为射线的交点．

(1)如图②，将绕点A旋转，当C、D、E在同一条直线上时，连接、，求证：且．

(2)若，把绕点A旋转，

①当时，求的长；

②旋转过程中线段长的最小值是_______．

13．如图1，中，是角平分线，点E、F分别在边AC、BC上，、将绕点C按逆时针方向旋转，使得EF所在直线交线段AD于点M，交线段AB于点N．

(1)当旋转75°时，如图2，直线EF与AD的位置关系是______，______°；

(2)在旋转一周过程中，试探究：当CE旋转多少度时，中有两个角相等．

14．菱形的对角线，交于点O．

(1)如图1，过菱形的顶点A作于点E，交于点H，若，求的长；

(2)如图2，过菱形的顶点A作，且，线段交于点H，交于点E．当D，C，F三点在同一直线上时，求证：；

(3)如图3，菱形中，，点P为直线上的动点，连接，将线段绕点B逆时针旋转60°得到线段，连接，当线段的长度最小时，直接写出的度数．

15．（1）阅读理解

利用旋转变换解决数学问题是一种常用的方法．如图1，点P是等边三角形ABC内一点，PA＝1，，PC＝2．求∠BPC的度数．

为利用已知条件，不妨把△BPC绕点C顺时针旋转60°得，连接．利用这种变换可以求∠BPC的度数，请写出推理过程；

（2）类比迁移

如图2，点P是等腰Rt△ABC内一点，∠ACB＝90°，PA＝2，，PC＝1．求∠APC的度数．

16．为等边三角形，AB＝8，AD⊥BC于点D，E为线段AD上一点，．以AE为边在直线AD右侧构造等边三角形AEF，连接CE，N为CE的中点．

(1)如图1，EF与AC交于点G，连接NG，BE，直接写出NG与BE的数量关系；

(2)如图2，将绕点A逆时针旋转，旋转角为，M为线段EF的中点，连接DN，MN．当时，猜想∠DNM的大小是否为定值，如果是定值，请写出∠DNM的度数并证明，如果不是，请说明理由；

(3)连接BN，在绕点A逆时针旋转过程中，请直接写出线段BN的最大值．

17．如图1，在Rt△ABC中，∠ACB＝90°，AB＝10，BC＝6．D、E分别是AB、AC边的中点，连接DE．现将△ADE绕A点逆时针旋转，连接BD，CE并延长交于点F．

(1)如图2，点E正好落在AB边上，CF与AD交于点P．

①求证：AE•AB＝AD•AC；

②求BF的长；

(2)如图3，若AF恰好平分∠DAE，直接写出CE的长．

18．如图①，在ABC中，∠ACB＝90°，∠ABC＝30°，AC＝1，D为ABC内部的一动点（不在边上），连接BD，将线段BD绕点D逆时针旋转60°，使点B到达点F的位置；将线段AB绕点B顺时针旋转60°，使点A到达点E的位置，连接AD，CD，AE，AF，BF，EF．

(1)求证：BDA≌BFE；

(2)当CD+DF+FE取得最小值时，求证：ADBF．

(3)如图②，M，N，P分别是DF，AF，AE的中点，连接MP，NP，在点D运动的过程中，请判断∠MPN的大小是否为定值．若是，求出其度数；若不是，请说明理由．

参考答案：

1．(1)

(2)

(3)，，

2．(1)30°

(3)135°，315°

3．(1)40，BE＝AD

(2)①存在，②60°

(3)当α＝150°或330°时，的面积最大

4．(1)①；②

(2)AD＝BC，

(3)旋补中线长为，

5．(1)

(2)，

(3)α的值为30°或150°，

6． (2)；

(3)30

7．（Ⅰ）；垂直；平行；（Ⅱ）；（Ⅲ）或

8．（2）15°；（3）存在，或

9．（1）E（4，2）；

（2）60°；

（3）；

（4）点H不在此抛物线上．

10． (2)成立，

(3)不成立，，

11．(1)

(2)；

(3)；，

12． (2)①或；②

13．(1)垂直，60

(2)当CE旋转45°，90°，270°，315°时，△AMN中有两个角相等

14．(1)

(3)

15．（2）90°

16．(1)

(2)∠DNM的大小是定值，为120°

(3)

17．(1)②4

(2)

18． (3)∠MPN的值为定值，30°．