2022-2023学年天津五十五中八年级（上）期中数学试卷（含答案解析）

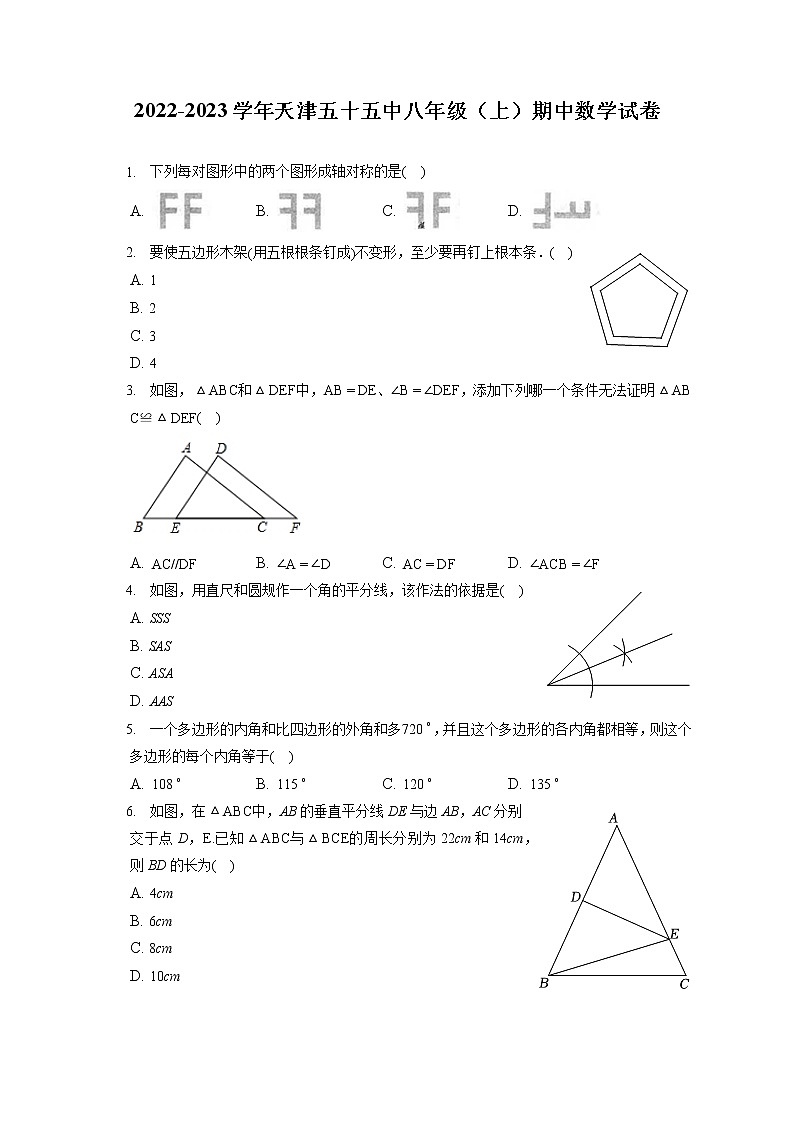
这是一份2022-2023学年天津五十五中八年级（上）期中数学试卷（含答案解析），共17页。试卷主要包含了【答案】C，【答案】B，【答案】A，【答案】D等内容，欢迎下载使用。

下列每对图形中的两个图形成轴对称的是( )
A. B. C. D.
要使五边形木架(用五根根条钉成)不变形，至少要再钉上根本条．( )
A. 1
B. 2
C. 3
D. 4
如图，△ABC和△DEF中，AB=DE、∠B=∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF( )
A. AC//DFB. ∠A=∠DC. AC=DFD. ∠ACB=∠F
如图，用直尺和圆规作一个角的平分线，该作法的依据是( )
A. SSS
B. SAS
C. ASA
D. AAS
一个多边形的内角和比四边形的外角和多720∘，并且这个多边形的各内角都相等，则这个多边形的每个内角等于( )
A. 108∘B. 115∘C. 120∘D. 135∘
如图，在△ABC中，AB的垂直平分线DE与边AB，AC分别交于点D，E.已知△ABC与△BCE的周长分别为22cm和14cm，则BD的长为( )
A. 4cm
B. 6cm
C. 8cm
D. 10cm
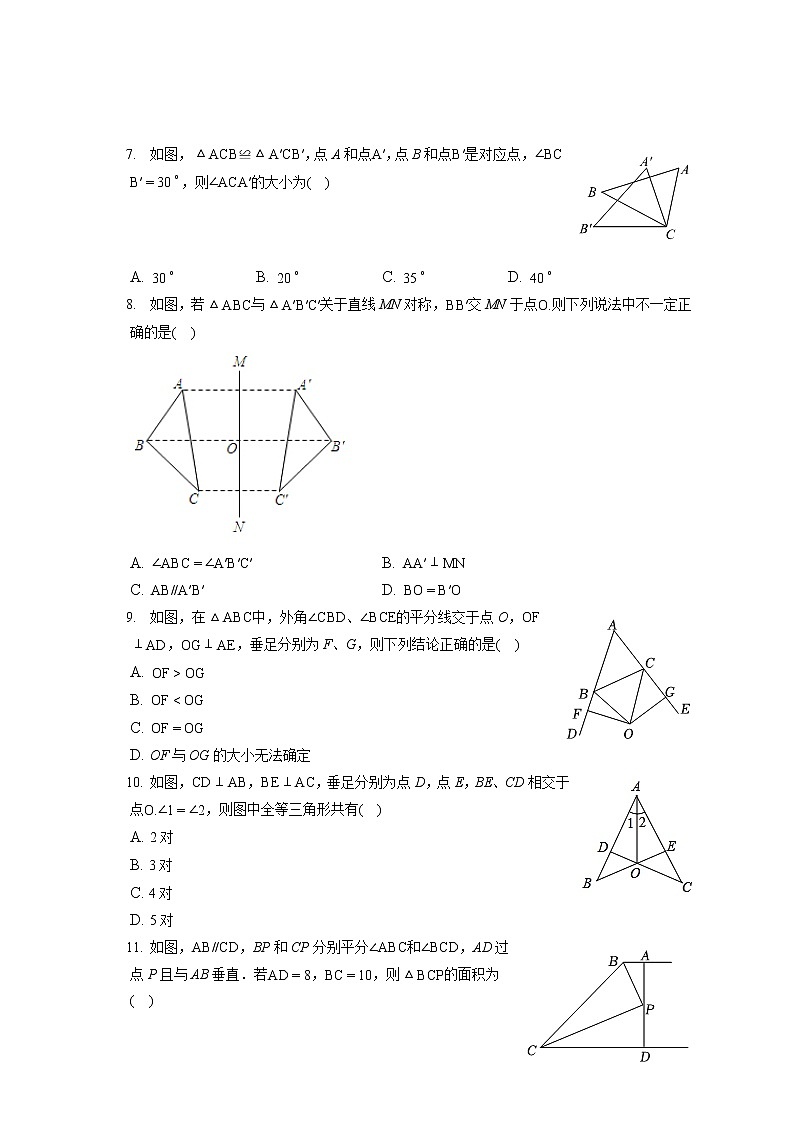
如图，△ACB≌△A′CB′，点A和点A′，点B和点B′是对应点，∠BCB′=30∘，则∠ACA′的大小为( )
A. 30∘B. 20∘C. 35∘D. 40∘
如图，若△ABC与△A′B′C′关于直线MN对称，BB′交MN于点O.则下列说法中不一定正确的是( )
A. ∠ABC=∠A′B′C′B. AA′⊥MN
C. AB//A′B′D. BO=B′O
如图，在△ABC中，外角∠CBD、∠BCE的平分线交于点O，OF⊥AD，OG⊥AE，垂足分别为F、G，则下列结论正确的是( )
A. OF>OG
B. OFC. OF=OG
D. OF与OG的大小无法确定
如图，CD⊥AB，BE⊥AC，垂足分别为点D，点E，BE、CD相交于点O.∠1=∠2，则图中全等三角形共有( )
A. 2对
B. 3对
C. 4对
D. 5对
如图，AB//CD，BP和CP分别平分∠ABC和∠BCD，AD过点P且与AB垂直．若AD=8，BC=10，则△BCP的面积为( )
A. 16
B. 20
C. 40
D. 80
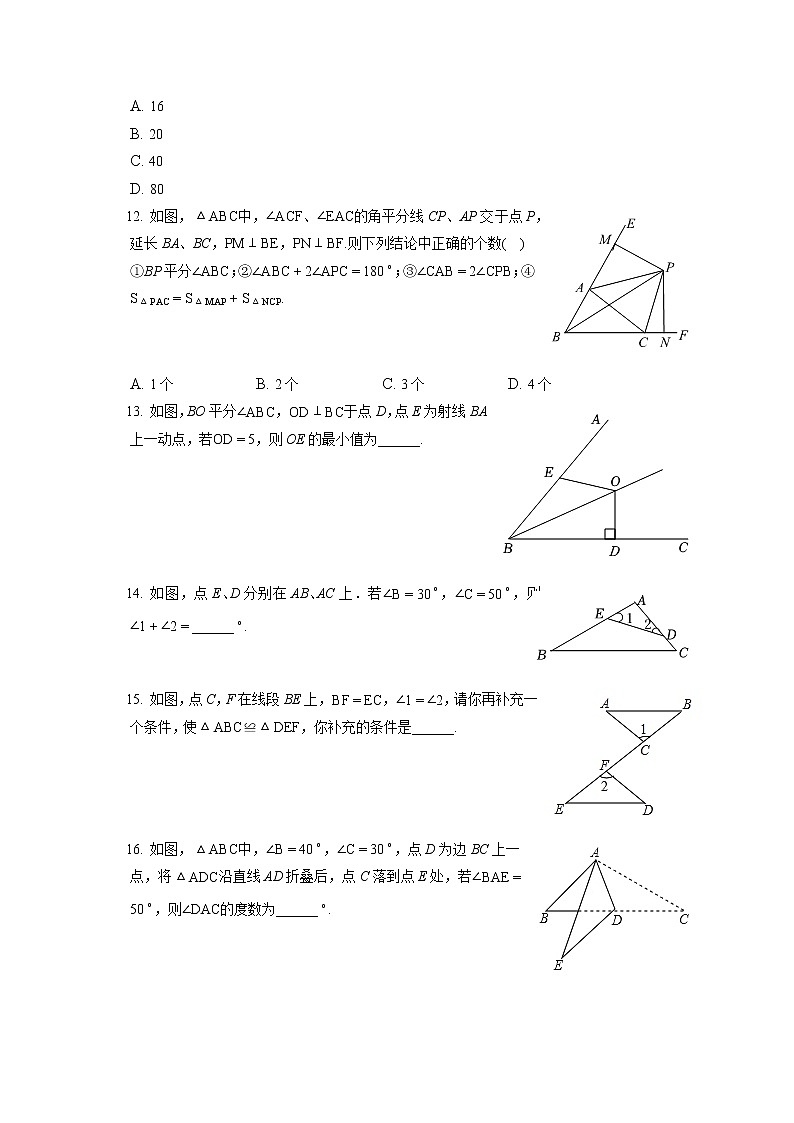
如图，△ABC中，∠ACF、∠EAC的角平分线CP、AP交于点P，延长BA、BC，PM⊥BE，PN⊥BF.则下列结论中正确的个数( )
①BP平分∠ABC；②∠ABC+2∠APC=180∘；③∠CAB=2∠CPB；④S△PAC=S△MAP+S△NCP.
A. 1个B. 2个C. 3个D. 4个
如图，BO平分∠ABC，OD⊥BC于点D，点E为射线BA上一动点，若OD=5，则OE的最小值为______.
如图，点E、D分别在AB、AC上．若∠B=30∘，∠C=50∘，则∠1+∠2=______∘.
如图，点C，F在线段BE上，BF=EC，∠1=∠2，请你再补充一个条件，使△ABC≌△DEF，你补充的条件是______.
如图，△ABC中，∠B=40∘，∠C=30∘，点D为边BC上一点，将△ADC沿直线AD折叠后，点C落到点E处，若∠BAE=50∘，则∠DAC的度数为______∘.
如图，在△ABC中，AD是∠BAC的平分线，延长AD至E，使AD=DE，若AB=3AC，△BDE的面积为9，则△ABC的面积是______.
如图，P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补．若∠MPN在绕点P旋转的过程中，其两边分别与OA，OB相交于M，N两点，则以下结论：(1)PM=PN恒成立；(2)OM+ON的值不变；(3)四边形PMON的面积不变．其中结论正确的有______.
如图，在△ABC与△DEF中，如果AB=DE，BE=CF，∠ABC=∠DEF；求证：AC//DF.
如图，已知在△ABC中，高AD，∠BAC角平分线为AE，若∠B=32∘，∠ACD=54∘，求∠EAD的度数．
在如图所示的正方形网格中，已有两个正方形涂黑，请再将其中的两个空白正方形涂黑，使涂黑部分图形是一个轴对称图形(请画出三种不同图形).
如图，在△ABC中，点D在边BC上，CD=AB，DE//AB，∠DCE=∠A.求证：DE=BC.
如图①：△ABC中，AC=BC，延长AC到E，过点E作EF⊥AB交AB的延长线于点F，延长CB到G，过点G作GH⊥AB交AB的延长线于H，且EF=GH.
(1)求证：△AEF≌△BGH；
(2)如图②，连接EG与FH相交于点D，若AB=4，求DH的长．
在△ABC中，∠ACB=90∘，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时，
求证：①△ADC≌△CEB；②DE=AD+BE；
(2)当直线MN绕点C旋转到图2的位置时，(1)中的结论还成立吗？若成立，请给出证明；若不成立，说明理由．
答案和解析
1.【答案】C
【解析】解：A、不是轴对称图形，故本选项不合题意；
B、不是轴对称图形，故本选项不合题意；
C、是轴对称图形，故本选项符合题意；
D、不是轴对称图形，故本选项不合题意；
故选：C.
根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形可得答案．
此题主要考查了轴对称图形，关键是掌握轴对称图形的概念，找出图形的对称轴．
2.【答案】B
【解析】解：如图，至少需要2根木条．
故选：B.
根据三角形的稳定性，添加的木条把五边形分成三角形即可．
本题考查三角形稳定性的实际应用．三角形的稳定性在实际生活中有着广泛的应用，如钢架桥、房屋架梁等，因此要使一些图形具有稳定的结构，往往通过连接辅助线转化为三角形而获得．
3.【答案】C
【解析】
【分析】
本题考查了全等三角形的判定定理，证明三角形全等的方法有：SSS，SAS，ASA，AAS，还有直角三角形的HL定理．根据全等三角形的判定定理，即可得出答．
【解答】
解：∵AB=DE，∠B=∠DEF，
∴添加AC//DF，得出∠ACB=∠F，即可证明△ABC≌△DEF，故A、D都正确；
当添加∠A=∠D时，根据ASA，也可证明△ABC≌△DEF，故B正确；
但添加AC=DF时，没有SSA定理，不能证明△ABC≌△DEF，故C不正确；
故选C.

4.【答案】A
【解析】解：如图，连接BC，AC，
由作图知：在△OAC和△OBC中，
OA=OBOC=OCAC=BC，
∴△OAC≌△OBC(SSS)，
故选：A.
根据题意易知：OB=OA，BC=AC，OC=OC，因此符合SSS的条件．
本题考查的是全等三角形的判定，解题的关键是要清楚作图时作出的线段OB与OA、BC与AC是相等的．
5.【答案】D
【解析】解：设这个多边形边数为n，
由题意得：(n−2)×180∘−360∘=720∘，
∴n=8，
∵这个多边形的每个内角都相等，
∴它每一个内角的度数为：180∘−360∘÷8=135∘，
故选：D.
由多边形的内角和定理，外角和是360∘，即可求解．
本题考查多边形的有关知识，关键是掌握多边形的内角和定理：(n−2)⋅180∘(n≥3且n为整数)；外角和是360∘.
6.【答案】A
【解析】解：∵DE是AB的垂直平分线，
∴EA=EB，AD=BD=12AB，
∵△BCE的周长是14cm，
∴BC+BE+EC=14cm，
∴BC+AE+EC=14cm，
∴AC+BC=14cm；
∵△ABC的周长是22cm，
∴AB+AC+BC=22cm，
∴AB=22−14=8(cm)，
∴BD=12AB=12×8=4(cm)，
故选：A.
根据线段垂直平分线的性质可得EA=EB，AD=BD=12AB，从而根据已知可得△BCE的周长=AC+BC=14cm，进而可得AB=8cm，然后进行计算即可解答．
本题考查了线段垂直平分线的性质，熟练掌握线段垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
7.【答案】A
【解析】解：∵△ACB≌△A′CB′，
∴∠ACB=∠A′CB′，
∴∠ACA′+∠A′CB=∠A′CB+∠BCB′，
∴∠ACA′=∠BCB′=30∘.
故选：A.
先根据全等三角形的性质得∠ACB=∠A′CB′，再两边减去∠A′CB即可得到∠ACA′=∠BCB′=30∘.
本题考查了全等三角形的性质，熟练掌握全等三角形的对应边相等；全等三角形的对应角相等是解题的关键．
8.【答案】C
【解析】
【分析】
本题考查轴对称的性质，平行线的判定，线段的垂直平分线的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
根据轴对称的性质解决问题即可．
【解答】
解：∵△ABC与△A′B′C′关于直线MN对称，BB′交MN于点O，
∴△ABC≌△A′B′C′，AA′⊥MN，OB=OB′，
∴∠ABC=∠A′B′C′，
故A，B，D正确，
故选C.
9.【答案】C
【解析】解：如图：过O作OM⊥BC于M，
∵OB平分∠CBD、OF⊥AD，OM⊥BC，
∴OF=OM，
∵OC平分∠BCE，OG⊥AE，OM⊥BC，
∴OG=OM，
∴OF=OG.
故选：C.
过O作OM⊥BC于M，再根据角平分线的性质即可得出：OF=OM，OM=OG，进而可以得出答案．
此题考查了角平分线的性质，能利用角平分线的性质正确作出辅助线是解题的关键．
10.【答案】C
【解析】解：∵CD⊥AB，BE⊥AC，AO平分∠BAC
∴∠ADO=∠AEO=90∘，∠DAO=∠EAO
∵AO=AO
∴△ADO≌△AEO；(AAS)
∴OD=OE，AD=AE
∵∠DOB=∠EOC，∠ODB=∠OEC=90∘
∴△BOD≌△COE；(ASA)
∴BD=CE，OB=OC，∠B=∠C
∵AE=AD，∠DAC=∠CAB，∠ADC=∠AEB=90∘
∴△ADC≌△AEB；(ASA)
∵AD=AE，BD=CE
∴AB=AC
∵OB=OC，AO=AO
∴△ABO≌△ACO.(SSS)
所以共有四对全等三角形．
故选：C.
共有四对．分别为△ADO≌△AEO，△ADC≌△AEB，△ABO≌△ACO，△BOD≌△COE.做题时要从已知条件开始结合图形利用全等的判定方法由易到难逐个寻找．
本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、SSA、HL.
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
11.【答案】B
【解析】解：过P作PE⊥BC于E，
∵AB//CD，
∴∠BAP+∠CDP=180∘，
∵AD⊥AB，
∴∠BAP=90∘，
∴∠CDP=90∘，
即AD⊥CD，
∵PE⊥BC，BP和CP分别平分∠ABC和∠BCD，
∴PA=PE，PE=PD，
∴PA=PD，
∵AD=8，
∴PE=PD=AP=4，
∵BC=10，
∴△BCP的面积为12×BC×PE=12×10×4=20.
故选：B.
过P作PE⊥BC于E，根据角平分线的性质得出PE=PA=PD，求出PE=PA=PD=12AD=4，再根据三角形的面积公式求出答案即可．
本题考查了平行线的性质和角平分线的性质，能熟记角平分线上的点到角两边的距离相等是解此题的关键．
12.【答案】D
【解析】解：过P作PQ⊥AC于Q，
∵∠ACF、∠EAC的角平分线CP、AP交于点P，PM⊥BE，PN⊥BF，
∴PM=PQ，PQ=PN，
∴PM=PN，
∴P在∠ABC的角平分线上，即BP平分∠ABC，故①正确；
∵PM⊥AB，PN⊥BC，PQ⊥AC，
∴∠PMA=∠PQA=90∘，∠PQC=∠PNC=90∘，
在Rt△PMA和Rt△PQA中，
PA=PAPM=PQ，
∴Rt△PMA≌Rt△PQA(HL)，
∴∠MPA=∠QPA，
同理Rt△PQC≌Rt△PNC，
∴∠QPC=∠NPC，
∵∠PMA=∠PNC=90∘，
∴∠ABC+∠MPN=360∘−90∘−90∘=180∘，
∴∠ABC+2∠APC=180∘，故②正确；
∵PC平分∠FCA，BP平分∠ABC，
∴∠FCA=∠ABC+∠CAB=2∠PCN，
又∵∠PCN=12∠ABC+∠CPB，
∴∠ABC+∠CAB=2(12∠ABC+∠CPB)，
∴∠CAB=2∠CPB，故③正确；
∵Rt△PMA≌Rt△PQA，Rt△PQC≌Rt△PNC，
∴S△PAC=S△MAP+S△NCP，故④正确；
即正确的个数是4，
故选：D.
过P作PQ⊥AC于Q，根据角平分线的性质得出PQ=PN，PQ=PM，求出PQ=PM=PN，求出∠PMA=∠PNC=∠PQA=∠PQC=90∘，根据全等三角形的判定得出Rt△PMA≌Rt△PQA，Rt△PQC≌Rt△PNC，再逐个判断即可．
本题考查了角平分线的性质和全等三角形的性质和判定，掌握角平分线上的点到角两边的距离相等是解此题的关键．
13.【答案】5
【解析】解：∵BO平分∠ABC，OD⊥BC于点D，OD=5，
∴O到AB的距离等于OD的长，
根据垂线段最短，可知OE最小值为5.
故答案为：5.
利用角平分线的性质即可，
本题考查了角平分线上的点到角的两边的距离相等的性质，利用垂线段最短是关键．
14.【答案】80
【解析】解：∵∠1+∠2+∠A=180∘，∠B+∠C+∠A=180∘，
∴∠1+∠2=∠B+∠C，
∵∠B=30∘，∠C=50∘，
∴∠1+∠2=∠B+∠C=30∘+50∘=80∘.
故答案为：80∘.
根据三角形的内角和定理列式整理可得∠1+∠2=∠B+∠C，从而可求解．
本题考查了三角形的内角和定理，是基础题，解答的关键是熟记三角形的内角和为180∘.
15.【答案】FD=AC(答案不唯一)
【解析】解：添加FD=AC，
∵BF=EC，
∴BF−CF=EC−CF
∴BC=EF
在△ABC与△DEF中，
BC=EF∠1=∠2AC=DF
∴△ABC≌△DEF(SAS)
故答案为：FD=AC(答案不唯一)
已知△ABC与△DEF中有一组边与一组角相等，根据全等三角形的判定可知，只需要添加一组边或一组角即可全等．
本题考查全等三角形的判定，解题的关键是熟练全等三角形的判定条件，本题属于基础题型．
16.【答案】30
【解析】解：∵∠B=40∘，∠C=30∘，
∴∠BAC=110∘，
∵∠BAE=50∘，
∴∠CAE=60∘，
∵△ADC沿直线AD折叠得到△ADE，
∴∠CAD=∠EAD=30∘，
故答案为：30.
根据三角形内角和定理可得∠BAC=110∘，可得∠CAE=60∘，由折叠的性质可得∠CAD=∠EAD=30∘.
本题考查三角形内角和定理，折叠的性质，解题的关键是明确折叠前后对应的角相等．
17.【答案】12
【解析】解：如图，过点D作DG⊥AC，交AC的延长线于G，DH⊥AB于H，
∵AD=DE，△BDE的面积为9，
∴S△ABD=S△BDE=9，
∵AD是∠BAC的平分线，DH⊥AB，DG⊥AC，
∴DG=DH，
∵AB=3AC，
∴S△ABD=3S△ACD，
∴S△ACD=3，
∴S△ABC=S△ABD+S△ACD=9+3=12，
故答案为：12.
过点D作DG⊥AC，交AC的延长线于G，DH⊥AB于H，由角平分线的性质可得DG=DH，求出△ABD的面积，再求出△ADC的面积，最后求出答案即可．
本题考查了角平分线的性质，三角形的面积公式，添加恰当辅助线是解题的关键．
18.【答案】(1)(2)(3)
【解析】解：如图，作PE⊥OA于E，PF⊥OB于F.
∵∠PEO=∠PFO=90∘，
∴∠EPF+∠AOB=180∘，
∵∠MPN+∠AOB=180∘，
∴∠EPF=∠MPN，
∴∠EPM=∠FPN，
∵OP平分∠AOB，PE⊥OA于E，PF⊥OB于F，
∴PE=PF，
在△POE和△POF中，
PE=PFOP=OP，
∴Rt△POE≌Rt△POF(HL)，
∴OE=OF，
在△PEM和△PFN中，
∠MPE=∠NPEPE=PF∠PEM=∠PFN，
∴△PEM≌△PFN(ASA)，
∴EM=NF，PM=PN，S△PEM=S△PNF，故(1)正确．
∴S四边形PMON=S四边形PEOF=定值，故(3)正确．
OM+ON=OE+ME+OF−NF=2OE=定值，故(2)正确．
故答案为：(1)(2)(3).
作PE⊥OA于E，PF⊥OB于F，根据OP平分∠AOB可知PE=PF，结合OP=OP即可证明△POE≌△POF.根据图中各角的数量关系可得∠MPE=∠NPF、∠PEM=∠PFN，进而还可证明△PEM≌△PFN；利用全等三角形的性质可以得到多组相等的边，由此判断(1)的正误．根据全等三角形的性质得到S△PEM=S△PNF，据此可得S四边形PMON=S四边形PEOF=定值，还可判断(3)的正误；由线段和差关系可得OM+ON=2OE=定值，故(2)正确，即可求解．
本题考查了全等三角形的判定和性质，角平分线的性质等知识，添加辅助线构造全等三角形是解题的关键．
19.【答案】证明：∵BE=CF，
∴BC=EF，
在△ABC和△DEF中，
AB=DE∠ABC=∠DEFBC=EF，
∴△ABC≌△DEF(SAS)，
∴∠ACB=∠DFE，
∴AC//DF.
【解析】首先利用等式的性质得BC=EF，再利用SAS证明△ABC≌△DEF，得∠ACB=∠DFE，从而有AC//DF.
本题主要考查了全等三角形的判定与性质，平行线的判定等知识，熟练掌握全等三角形的判定与性质是解题的关键．
20.【答案】解：∵AD为高，∠B=32∘，
∴∠BAD=58∘，
∵∠ACD=54∘，
∴∠BAC=∠ACD−∠B=22∘，
∵AE是角平分线，
∴∠BAE=12∠BAC=11∘，
∴∠EAD=∠BAD−∠BAE=58∘−11∘=47∘，
答：∠EAD的度数为47∘.
【解析】根据高、角平分线的定义以及三角形内角和定理计算即可．
本题考查的是三角形内角和定理，掌握三角形的内角和等于180∘是解题的关键．
21.【答案】解：如图：图1，图2，图3为所求；

【解析】根据轴对称图形的定义即可解决问题．
本题考查了轴对称图形的概念，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
22.【答案】证明：∵DE//AB，
∴∠EDC=∠B，
在△CDE和△ABC中，
∠EDC=∠BCD=AB∠DCE=∠A，
∴△CDE≌△ABC(ASA)，
∴DE=BC.
【解析】利用平行线的性质得∠EDC=∠B，再利用ASA证明△CDE≌△ABC，可得结论．
本题主要考查了平行线的性质，全等三角形的判定与性质等知识，熟练掌握全等三角形的判定与性质是解题的关键．
23.【答案】(1)证明：∵AC=BC，
∴∠A=∠ABC.
∵∠ABC=∠GBH，
∴∠A=∠GBH.
∵EF⊥AB，GH⊥AB，
∴∠AFE=∠BHG.
在△ADG和△CDF中，
∠A=∠GBH∠AFE=∠BHGEF=GH，
∴△AEF≌△BGH(AAS).
(2)解：∵△AEF≌△BGH，
∴AF=BH，
∴AB=FH=4.
∵EF⊥AB，GH⊥AB，
∴∠EFD=∠GHD.
在△EFD和△GHD中，
∠EFD=∠GHD∠EDF=∠GDHEF=GH
∴△EFD≌△GHD(AAS)，
∴DH=DF=12FH=12AB=2.
【解析】(1)利用AAS即可证明△AEF≌△BGH；
(2)结合(1)证明△EFD≌△GHD，即可解决问题．
本题考查了全等三角形的判定与性质，解决本题的关键是得到△EFD≌△GHD.
24.【答案】(1)证明：①∵∠ACD+∠BCE=90∘，
∠DAC+∠ACD=90∘，
∴∠DAC=∠ECB，
又AC=BC，∠ADC=∠CEB=90∘，
∴△ADC≌△CEB(AAS).
②∵△ADC≌△CEB，
∴CD=BE，AD=CE.
∴DE=CE+CD=AD+BE.
(2)直线MN绕点C旋转到图2的位置时，△ADC≌△CEB成立，但DE=AD+BE不成立，此时应有DE=AD−BE.
证明：∵∠ACD+∠BCE=90∘，
∠DAC+∠ACD=90∘，
∴∠DAC=∠BCE.
又AC=BC，∠ADC=∠BEC=90∘，
在△ADC和△CEB中，
∠ADC=∠BEC∠DAC=∠ECBAC=CB
∴△ADC≌△CEB(AAS).
∴CD=BE，AD=CE.
∴DE=CE−CD=AD−BE.
【解析】分析：
(1)直角三角形中斜边对应相等，即可证明全等，再由线段对应相等，得出②中结论；
(2)由图可知，△ADC与△CEB仍全等，但线段的关系已发生改变．
本题考查了三角形全等的判定及性质；熟练掌握全等三角形的性质和判定，此题作为选择或填空很容易漏掉后一问，注意运用．