

上海市嘉定区2022-2023学年九年级上学期期中数学试卷(含答案)
展开2022-2023学年上海市嘉定区九年级(上)期中数学试卷
一、选择题(本大题共6题,每题4分,满分24分)
1.下列图形一定是相似图形的是( )
A.两个矩形 B.两个等腰三角形
C.两个直角三角形 D.两个正方形
2.如图,在Rt△ABC中,∠C=90°,BC=4,AC=2,则tanA等于( )
A. B.2 C. D.
3.如果两个三角形相似,其中一个三角形的两个内角分别为82°、53°,那么另一个三角形中最小的内角为 ( )
A.82° B.53° C.45° D.不能确定
4.如图:在△ABC中,点D、E分别在AB、AC上,根据下列给定的条件,不能判断DE与BC平行的是( )
A. B. C. D.
5.已知线段a,b,c,求作线段x,使ax=bc,下列作图中正确的是( )
A. B.
C. D.
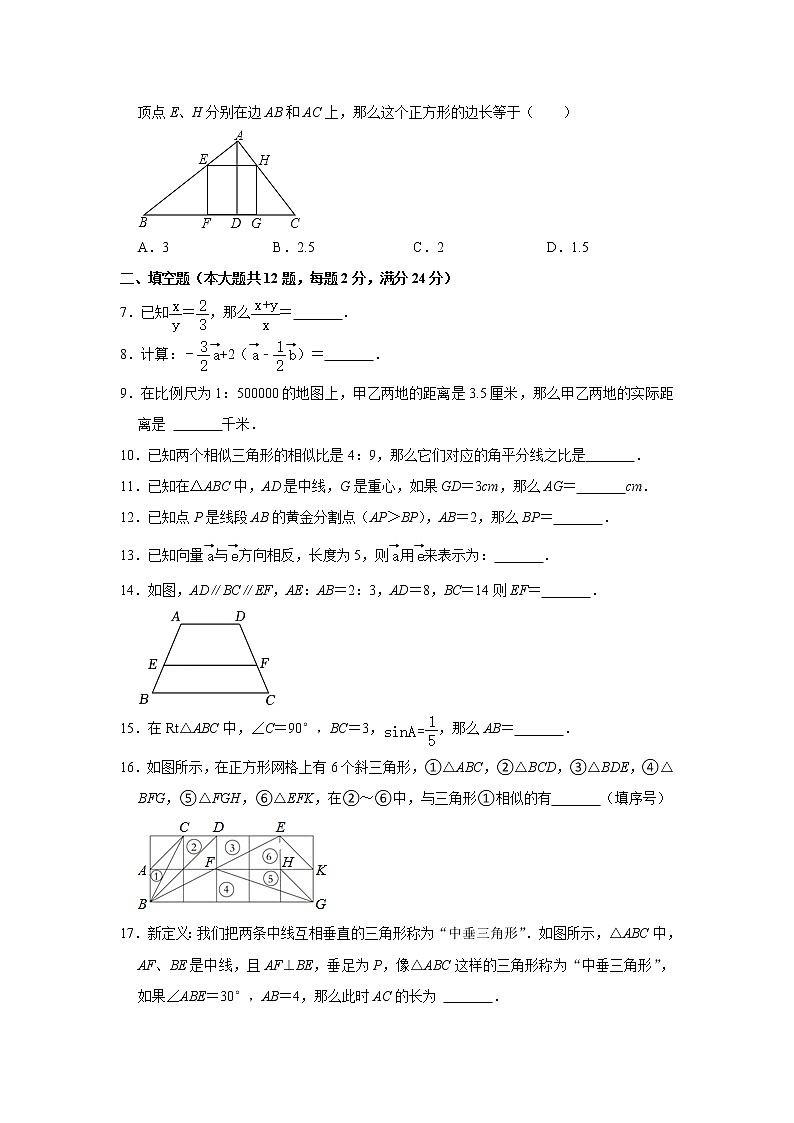
6.如图,已知在△ABC中,边BC=6,高AD=3,正方形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,那么这个正方形的边长等于( )
A.3 B.2.5 C.2 D.1.5
二、填空题(本大题共12题,每题2分,满分24分)
7.已知=,那么= .
8.计算:﹣+2(﹣)= .
9.在比例尺为1:500000的地图上,甲乙两地的距离是3.5厘米,那么甲乙两地的实际距离是 千米.
10.已知两个相似三角形的相似比是4:9,那么它们对应的角平分线之比是 .
11.已知在△ABC中,AD是中线,G是重心,如果GD=3cm,那么AG= cm.
12.已知点P是线段AB的黄金分割点(AP>BP),AB=2,那么BP= .
13.已知向量与方向相反,长度为5,则用来表示为: .
14.如图,AD∥BC∥EF,AE:AB=2:3,AD=8,BC=14则EF= .
15.在Rt△ABC中,∠C=90°,BC=3,,那么AB= .
16.如图所示,在正方形网格上有6个斜三角形,①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK,在②~⑥中,与三角形①相似的有 (填序号)
17.新定义:我们把两条中线互相垂直的三角形称为“中垂三角形”.如图所示,△ABC中,AF、BE是中线,且AF⊥BE,垂足为P,像△ABC这样的三角形称为“中垂三角形”,如果∠ABE=30°,AB=4,那么此时AC的长为 .
18.如图,在△ABC中,MN∥AC,直线MN将△ABC分割成面积相等的两部分.将△BMN沿直线MN翻折,点B恰好落在点E处,连接AE,若AE∥CN,则AE:NC= .
三、解答题(78分)
19.(10分)已知==≠0,且5x+y﹣2z=10,求x、y、z值
20.(10分)计算:+cot30°﹣.
21.(10分)如图,已知在△ABC中,AD是边BC上的中线,设=,=;
(1)求(用向量,的式子表示);
(2)如果点E在中线AD上,求作在,方向上的分向量;(不要求写作法,但要保留作图痕迹,并指出所作图中表示结论的分向量).
22.(10分)如图,在▱ABCD中,点E是线段CD延长线上的一点,BE与AD交于F点.
(1)求证:△ABF∽△CEB;
(2)若DF:AF=2:3,且S△DEF=4,求▱ABCD的面积.
23.(12分)已知:如图,在△ABC中,点D、E分别在边AB、AC上,且∠ABE=∠ACD,BE、CD交于点G.
(1)求证:△AED∽△ABC;
(2)如果BE平分∠ABC,求证:DE=CE.
24.(12分)已知:如图,在四边形ABCD中,∠A=90°,BD⊥DC,且BD2=AD•BC,
点M是边BC的中点.
(1)求证:AD∥BC;
(2)作BE⊥DM,垂足为点E,并交CD于点F.求证:2AD•DM=DF•DC.
25.(8分)如图,在等腰梯形ABCD中,AD∥BC,AD=2,AB=5,sin∠B=,点E是边BC上的一个动点(不与点B、C重合),作∠AEF=∠AEB,使边EF交边CD与点F(不与点C、D重合),设BE=x,CF=y.
(1)求边BC的长:
(2)当△ABE与△CEF相似时,求BE的长:
(3)求y关于x的函数关系式,并写出定义域.
2022-2023学年上海市嘉定区九年级(上)期中数学试卷
(参考答案与详解)
一、选择题(本大题共6题,每题4分,满分24分)
1.下列图形一定是相似图形的是( )
A.两个矩形 B.两个等腰三角形
C.两个直角三角形 D.两个正方形
【分析】根据相似图形的定义,结合选项,用排除法求解.
【解答】解:A、两个矩形,对应角相等,对应边不一定成比例,故不符合题意;
B、两个等腰三角形顶角不一定相等,故不符合题意.
C、两个直角三角形,只有一个直角相同,锐角不一定相等,故不符合题意;
D、两个正方形,形状相同,大小不一定相同,符合相似性定义,故符合题意;
故选:D.
2.如图,在Rt△ABC中,∠C=90°,BC=4,AC=2,则tanA等于( )
A. B.2 C. D.
【分析】根据正切的定义计算,得到答案.
【解答】解:在Rt△ABC中,∠C=90°,
∴tanA==2,
故选:B.
3.如果两个三角形相似,其中一个三角形的两个内角分别为82°、53°,那么另一个三角形中最小的内角为 ( )
A.82° B.53° C.45° D.不能确定
【分析】先求出该三角形的另一个内角的度数,再由相似三角形的性质即可得出结论.
【解答】解:∵一个三角形的两个内角分别为82°、53°,
∴另一个内角=180°﹣82°﹣53°=45°.
∵两个三角形相似,
∴另一个三角形中最小的内角为45°.
故选:C.
4.如图:在△ABC中,点D、E分别在AB、AC上,根据下列给定的条件,不能判断DE与BC平行的是( )
A. B. C. D.
【分析】根据平行线分线段成比例定理的逆定理,即“三条直线被两条直线所截,如果截得的对应线段成比例,那么三条直线平行”,进行分析判断即可.
【解答】解:∵,∴DE∥BC,A不合题意;
∵,∴DE∥BC,B不合题意;
∵,∴DE∥BC,C不合题意;
,不能判断DE与BC平行,D符合题意;
故选:D.
5.已知线段a,b,c,求作线段x,使ax=bc,下列作图中正确的是( )
A. B.
C. D.
【分析】利用ax=bc得比例式,与已知图形作对比,可以得出结论.
【解答】解:A、由ax=bc得,但x是所求线段,所以图形不能画出,故选项A不正确;
B、由ax=bc得,故选项B不正确;
C、由ax=bc得,故选项C正确;
D、由得ac=bx,与已知不符合,故选项D不正确;
故选:C.
6.如图,已知在△ABC中,边BC=6,高AD=3,正方形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,那么这个正方形的边长等于( )
A.3 B.2.5 C.2 D.1.5
【分析】利用正方形的性质可知EH∥BC,再利用平行线分线段成比例定理的推论可得△AHE∽△ACB,利用相似三角形的性质可得比例线段,利用比例线段可求正方形的边长
【解答】解:∵四边形EFMN是正方形,
∴EH∥BC,EH=EF,
∴△AEH∽△ABC,
又∵AD⊥BC,
∴AD⊥BC,EH=EF=MD,
∴=,
设EH=x,则AM=3﹣x,
∴=,
解得:x=2,
∴EH=2.
答:这个正方形的边长为2.
故选:C.
二、填空题(本大题共12题,每题2分,满分24分)
7.已知=,那么= .
【分析】直接利用已知得出x=y,进而得出答案.
【解答】解:∵=,
∴x=y,
∴==.
故答案为:.
8.计算:﹣+2(﹣)= ﹣ .
【分析】去括号合并同类向量即可.
【解答】解:﹣+2(﹣)=﹣+2﹣=﹣.
故答案为:﹣.
9.在比例尺为1:500000的地图上,甲乙两地的距离是3.5厘米,那么甲乙两地的实际距离是 17.5 千米.
【分析】根据比例尺=图上距离:实际距离,列比例式即可求得甲乙两地的实际距离.要注意统一单位.
【解答】解:设甲乙两地的实际距离为x厘米,
根据题意得,1:500000=3.5:x,
解得x=1750000,
12000000厘米=17.5千米.
即甲乙两地的实际距离为17.5千米.
故答案为:17.5.
10.已知两个相似三角形的相似比是4:9,那么它们对应的角平分线之比是 4:9 .
【分析】直接根据相似三角形的性质即可得出结论.
【解答】解:∵两个相似三角形的相似比是4:9,
∴它们对应的角平分线之比是4:9.
故答案为:4:9.
11.已知在△ABC中,AD是中线,G是重心,如果GD=3cm,那么AG= 6 cm.
【分析】根据三角形重心的性质即可求出AG的长.
【解答】解:∵G是△ABC的重心,且AD是中线,
∴AG=2GD=6cm.
故答案为:6.
12.已知点P是线段AB的黄金分割点(AP>BP),AB=2,那么BP= 3﹣ .
【分析】根据黄金分割点的定义,知AP是较长线段;所以AP=AB,代入数据即可得出AP的长度,进而得出BP.
【解答】解:由于P为线段AB=2的黄金分割点,
且AP>BP,
则AP=a==﹣1.
BP=2﹣(﹣1)=;
故答案为:3﹣
13.已知向量与方向相反,长度为5,则用来表示为: =﹣且||=||=5 .
【分析】根据平面向量的方向性即可得出结论.
【解答】解:∵与方向相反,长度为5,
∴=﹣且||=||=5.
故答案为:=﹣且||=||=5.
14.如图,AD∥BC∥EF,AE:AB=2:3,AD=8,BC=14则EF= 12 .
【分析】过点A作AH∥DC,交EF于点G,利用平行四边形的判定可得四边形AGFD和四边形AHCD都是平行四边形,从而可得AD=GF=8,AD=CH=8,进而可得BH=6,然后证明A字模型相似三角形△AEG∽△ABH,从而利用相似三角形的性质可得EG=4,最后进行计算即可解答.
【解答】解:过点A作AH∥DC,交EF于点G,
∵AD∥BC∥EF,
∴四边形AGFD是平行四边形,四边形AHCD是平行四边形,
∴AD=GF=8,AD=CH=8,
∵BC=14,
∴BH=BC﹣CH=6,
∵EG∥BH,
∴∠AEG=∠B,∠AGE=∠AHB,
∴△AEG∽△ABH,
∴=,
∴=,
∴EG=4,
∴EF=EG+FG=4+8=12,
故答案为:12.
15.在Rt△ABC中,∠C=90°,BC=3,,那么AB= 15 .
【分析】根据锐角三角函数的定义得出sinA=,代入求出即可.
【解答】解:如图:
∵=,BC=3,
∴AB=5BC=15,
故答案为:15.
16.如图所示,在正方形网格上有6个斜三角形,①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK,在②~⑥中,与三角形①相似的有 ③④⑤ (填序号)
【分析】两三角形三条边对应成比例,两三角形相似,据此即可解答.
【解答】解:设每个小正方形的边长为1,则△ABC的各边长分别为1、、.则
②△BCD的各边长分别为1、、2;
③△BDE的各边长分别为2、2、2(为△ABC各边长的2倍);
④△BFG的各边长分别为5、、(为△ABC各边长的倍);
⑤△FGH的各边长分别为2、、(为△ABC各边长的倍);
⑥△EFK的各边长分别为3、、.
根据三组对应边的比相等的两个三角形相似得到与三角形①相似的是③④⑤.
故答案为③④⑤.
17.新定义:我们把两条中线互相垂直的三角形称为“中垂三角形”.如图所示,△ABC中,AF、BE是中线,且AF⊥BE,垂足为P,像△ABC这样的三角形称为“中垂三角形”,如果∠ABE=30°,AB=4,那么此时AC的长为 2 .
【分析】根据三角形中位线的性质,得到EF∥AB,EF=AB=2,再由勾股定理得到结果.
【解答】解:如图,连接EF,
∵AF、BE是中线,
∴EF是△CAB的中位线,
可得:EF=×4=2,
∵EF∥AB,
∴△PEF∽△ABP,
∴===,
在Rt△ABP中,
AB=4,∠ABP=30°,
∴AP=2,PB=2,
∴PF=1,PE=,
在Rt△APE中,
∴AE=,
∴AC=2,
故答案为:.
18.如图,在△ABC中,MN∥AC,直线MN将△ABC分割成面积相等的两部分.将△BMN沿直线MN翻折,点B恰好落在点E处,连接AE,若AE∥CN,则AE:NC= .
【分析】利用翻折变换的性质得出BE⊥MN,BE⊥AC,进而利用相似三角形的判定与性质得出对应边之间的比值与高之间关系,即可得出答案.
【解答】解:连接BE,交MN于点I,交AG于点Z,
∵将△BMN沿直线MN翻折,点B恰好落在点E处,
∴BE⊥MN于点I,
∵MN∥AC,
∴BE⊥AC于点Z,
设△EMN与边AC交于点F、G∵MN∥AC,
∴△BMN∽△BAC,
∴(BI:BZ)2 =S△BMN:S△BAC=1:2,
∴BI:BZ=1:,
∴ZI:BI=(﹣1):1,
∵△EMN是由△BMN翻折得到,
∴△EMN≌△BMN,
∴EI=BI,
∴ZI:EI=(﹣1):1,
∴==+1,
∴1+=+1,
∴EZ:ZI=:1,
∵AC∥MN,AE∥NC,
∴==,
∴=,
∴AE:NC=:1,
故答案为::1.
三、解答题(78分)
19.(10分)已知==≠0,且5x+y﹣2z=10,求x、y、z值
【分析】首先设x=2a,y=3a,z=4a,然后再代入5x+y﹣2z=10,可得a的值,进而可得答案.
【解答】解:设x=2a,y=3a,z=4a,
∵5x+y﹣2z=10,
∴10a+3a﹣8a=10,
5a=10,
a=2,
∴x=4,y=6,z=8.
20.(10分)计算:+cot30°﹣.
【分析】根据特殊角三角函数值,可得答案.
【解答】解:原式=+﹣
=2+﹣
=3﹣2+2
=+2.
21.(10分)如图,已知在△ABC中,AD是边BC上的中线,设=,=;
(1)求(用向量,的式子表示);
(2)如果点E在中线AD上,求作在,方向上的分向量;(不要求写作法,但要保留作图痕迹,并指出所作图中表示结论的分向量).
【分析】(1)由AD是边BC上的中线,=,可求得,然后由三角形法则,求得;
(2)利用平行四边形法则,即可求得在,方向上的分向量.
【解答】解:(1)∵AD是边BC上的中线,=,
∴==,
∴=﹣=﹣;
(2)如图,过点E作EM∥BC,EN∥AB,
则、分别是在,方向上的分向量.
22.(10分)如图,在▱ABCD中,点E是线段CD延长线上的一点,BE与AD交于F点.
(1)求证:△ABF∽△CEB;
(2)若DF:AF=2:3,且S△DEF=4,求▱ABCD的面积.
【分析】(1)根据平行四边形对角相等可得∠A=∠C,对边平行可得AB∥CD,根据两直线平行,内错角相等得到∠ABF=∠E,然后利用两角对应相等,两三角形相似即可证明.
(2)由于△BCE∽△FDE,可根据两三角形的相似比,求出△FDE的面积,也就求出了四边形BCDF的面积.同理可根据△DEF∽△AFB,求出△AFB的面积.由此可求出▱ABCD的面积.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,
∵AB∥CD,
∴∠ABF=∠E,
在△ABF和△CEB中,∠A=∠C,∠ABF=∠E,
∴△ABF∽△CEB;
(2)解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AD=BC,
∴△ABF∽△DEF,△CEB∽△DEF,
∵DF:AF=2:3,
∴DE:AB=DE:CD=2:3,
∴DE:CE=2:5,
∴FD:BC=2:5,
∴S△ABF:S△DEF=AF2:FD2,S△BCE:S△FDE=BC2:FD2,
∵DF:AF=2:3,S△DEF=4,
∴△ABF的面积为9,
∴△CEB的面积为25,
∴▱ABCD的面积=25﹣4+9=30.
23.(12分)已知:如图,在△ABC中,点D、E分别在边AB、AC上,且∠ABE=∠ACD,BE、CD交于点G.
(1)求证:△AED∽△ABC;
(2)如果BE平分∠ABC,求证:DE=CE.
【分析】(1)证明B、C、E、D四点共圆,得到∠ADE=∠ACB,即可解决问题.
(2)如图,作辅助线,证明EM=EF;由sinα=,sinα=,得到,根据ME=EF,即可解决问题.
【解答】(1)证明:∵∠ABE=∠ACD,
∴B、C、E、D四点共圆,
∴∠ADE=∠ACB,而∠A=∠A,
∴△AED∽△ABC.
(2)解:过点E作EM⊥AB,EF⊥BC;
∵BE平分∠ABC,
∴EM=EF;设∠ADE=∠ACB=α,
则sinα=,sinα=,
∴,而ME=EF,
∴DE=CE.
24.(12分)已知:如图,在四边形ABCD中,∠A=90°,BD⊥DC,且BD2=AD•BC,
点M是边BC的中点.
(1)求证:AD∥BC;
(2)作BE⊥DM,垂足为点E,并交CD于点F.求证:2AD•DM=DF•DC.
【分析】(1)由∠BAD=∠BDC=90°,BD2=AD•BC即得△ABD∽△DCB,然后利用相似三角形的性质和平行线的判定即可求解;
(2)利用已知条件证明△BDF∽△CDB,然后利用相似三角形的性质和直角三角形中斜边上中线的性质即可证明.
【解答】证明:(1)∵BD⊥DC,
∴∠BDC=90°,
∴∠A=∠BDC,
而BD2=AD•BC,
∴△ABD∽△DCB,
∴∠ADC=∠DBC,
∴AD∥BC;
(2)解:∵BE⊥DM,
∴∠DBF+∠BDM=90°,
而∠BDM+∠MDC=90°,
∴∠DBE=∠MDC,
又M是边BC的中点,
∴DM=BM=CM=BC,
∴∠MDC=∠DCM,
∴∠DBE=∠DCM,
∴△BDF∽△CDB,
∴BD2=DF•DC,
而BD2=AD•BC,
∴AD•BC=DF•DC,
∴2AD•DM=DF•DC.
25.(8分)如图,在等腰梯形ABCD中,AD∥BC,AD=2,AB=5,sin∠B=,点E是边BC上的一个动点(不与点B、C重合),作∠AEF=∠AEB,使边EF交边CD与点F(不与点C、D重合),设BE=x,CF=y.
(1)求边BC的长:
(2)当△ABE与△CEF相似时,求BE的长:
(3)求y关于x的函数关系式,并写出定义域.
【分析】(1)根据等腰梯形的性质,可得AD=MN; BM=CN;AB=DC=5,根据勾股定理,可得BM的长,根据线段的和差,可得答案;
(2)分类讨论,当∠AEB=∠FEC时,根据正切函数,可得ME的长,根据线段的和差,可得答案,当∠AEB=∠EFC时,根据等腰三角形的性质,可得BM与ME的关系,根据线段的和差,可得答案;
(3)根据相似三角形的性质,可得函数解析式,根据线段的和差,可得定义域.
【解答】解:(1)如图:过A作AM⊥BC,过D作DN⊥BC,
∵等腰梯形ABCD,AM⊥BC,DN⊥BC,sin∠B=,
∴AD=MN; BM=CN;AB=DC=5;∠B=∠C,
∴AM=AB•sin∠B=5×=3
∴BM=CN===4
∴BC=BM+MN+CN=AD+2BM=2+2×4=10;
(2)△ABE与△CEF相似有两种情况,如图:
①当∠AEB=∠FEC时
∵∠AEF=∠AEB
∴∠AEF=∠AEB=∠FEC=60°
过A作AM⊥BC
由(1)知:AM=3,BM=4
∴ME=AM•tan60°=3×=
∴BE=BM+ME=4+,
②当∠AEB=∠EFC时
∵∠AEF=∠AEB
∴∠AEF=∠EFC
∴AE∥DC
∴∠AEB=∠C=∠B
△ABE是等腰三角形
过A 作AM⊥BC
∴BM=ME(等腰三角形三线合一性质)
∵BM=4
∴BE=2BM=8
综上,当△ABE∽△CEF时,BE的长为4+或8;
(3)作图如下,
易知x>4,否则F点将在DC的延长线上或与C重合;
AG=3,GE=x﹣4
∵∠PAE=∠AEB=∠AEP
故PA=PE,三线合一,Q为AE的中点;
又∠AGE=∠PQA=90°;
故△AGE∽△PQE;则有
AP=
而DP=AP﹣2
又△DFP∽△CFE
故有:;CF=y,DF=5﹣y,CE=10﹣x;
整理即可得:y=;(4<x<10)
上海市嘉定区2023-2024学年九年级上学期期末数学试卷(一模): 这是一份上海市嘉定区2023-2024学年九年级上学期期末数学试卷(一模),文件包含上海市嘉定区2023-2024学年九年级上学期期末数学试卷一模pdf、答案docx等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。
2022-2023学年上海市嘉定区八年级上学期期末数学试卷: 这是一份2022-2023学年上海市嘉定区八年级上学期期末数学试卷,文件包含精品解析上海市嘉定区八年级上学期期末数学试卷原卷版docx、精品解析上海市嘉定区八年级上学期期末数学试卷解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
上海市嘉定区部分学校联考2022-2023学年九年级(上)期中数学试卷(解析版): 这是一份上海市嘉定区部分学校联考2022-2023学年九年级(上)期中数学试卷(解析版),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












