





- 中考数学复习专题2无刻度直尺作图精练课件 课件 1 次下载
- 中考数学复习专题3数学建模及应用精讲课件 课件 1 次下载
- 中考数学复习专题4数学抽象与函数性质探究精讲课件 课件 0 次下载
- 中考数学复习专题4数学抽象与函数性质探究精练课件 课件 0 次下载
- 中考数学复习专题5几何综合探究题精讲课件 课件 0 次下载
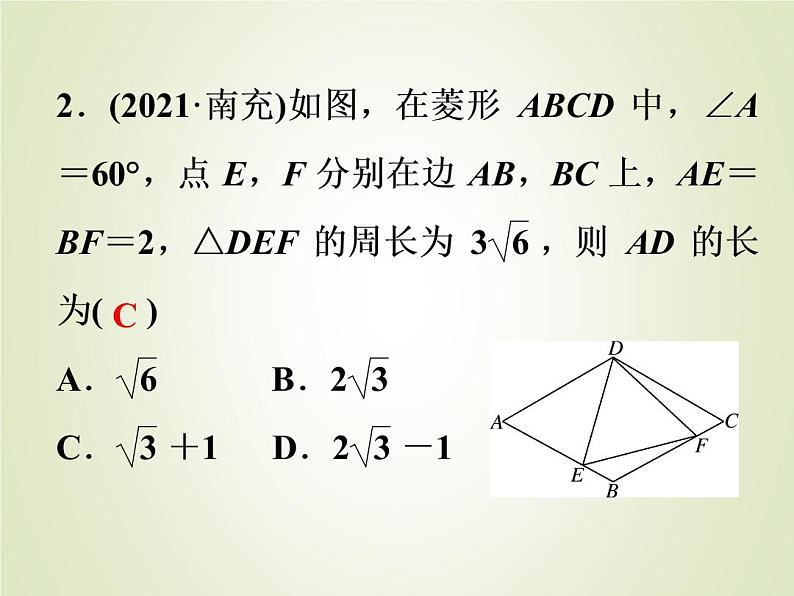
中考数学复习专题3数学建模及应用精练课件
展开1.(2021·绵阳)近年来,网购的蓬勃发展方便了人们的生活.某快递分派站现有包裹若干件需快递员派送,若每个快递员派送10件,还剩6件;若每个快递员派送12件,还差6件,那么该分派站现有包裹( )A.60件 B.66件 C.68件 D.72件
3.(2021·泰安)接种疫苗是阻断新冠病毒传播的有效途径,针对疫苗急需问题,某制药厂紧急批量生产,计划每天生产疫苗16万剂,但受某些因素影响,有10名工人不能按时到厂.为了应对疫情,回厂的工人加班生产,由原来每天工作8小时增加到10小时,每人每小时完成的工作量不变,这样每天只能生产疫苗15万剂.(1)求该厂当前参加生产的工人有多少人?(2)生产4天后,未到的工人同时到岗加入生产,每天生产时间仍为10小时.若上级分配给该厂共760万剂的生产任务,问该厂共需要多少天才能完成任务?
(2)每人每小时完成的数量为:16÷8÷40=0.05(万剂),设还需要生产y天才能完成任务,由题意可得:4×15+(30+10)×10×0.05y=760,解得:y=35,35+4=39(天),∴该厂共需要39天才能完成任务.
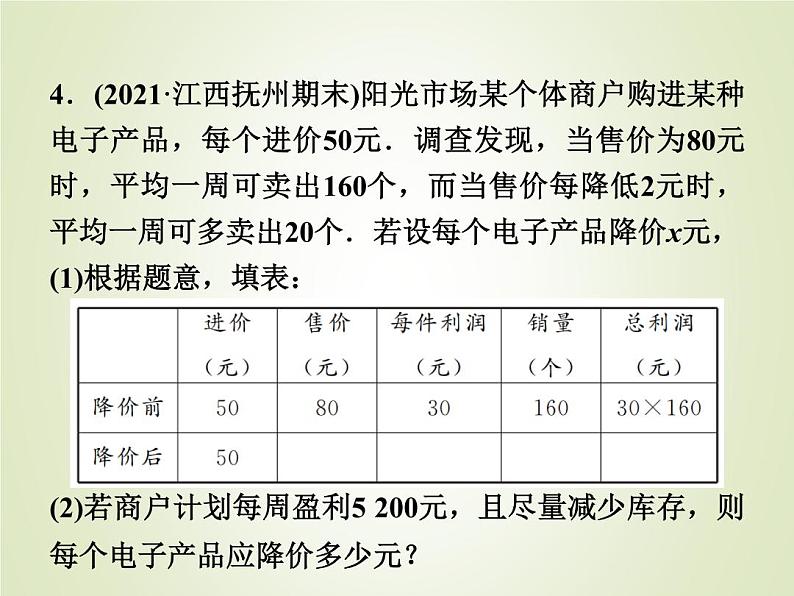
4.(2021·江西抚州期末)阳光市场某个体商户购进某种电子产品,每个进价50元.调查发现,当售价为80元时,平均一周可卖出160个,而当售价每降低2元时,平均一周可多卖出20个.若设每个电子产品降价x元,(1)根据题意,填表: (2)若商户计划每周盈利5 200元,且尽量减少库存,则每个电子产品应降价多少元?
5.(2021·江西模拟)某药店购进一批消毒液,进价为20元/瓶,要求利润率不低于20%,且不高于60%.该店通过分析销售情况,发现该消毒液一天的销售量y(瓶)与当天的售价x(元/瓶)满足下表所示的一次函数关系.
(1)若某天这种消毒液的售价为30元/瓶,求当天该消毒液的销售量.(2)如果某天销售这种消毒液获利192元,那么当天该消毒液的售价为多少元?(3)若客户在购买消毒液时,会购买相同数量(包)的口罩,且每包口罩的利润为20元,则当消毒液的售价定为多少时,可获得的日利润最大?最大日利润是多少元?
解:(1)设y与x的函数关系式为y=kx+b,解得:即y与x的函数关系式为y=-2x+80,∵20×(1+20%)=24(元),20×(1+60%)=32(元),∴x的取值范围为:24≤x≤32,将x=30代入y=-2x+80,得y=-2×30+80=20,答:当天该消毒液的销售量是20瓶;
(2)设售价为x元,(x-20)×(-2x+80)=192,解得,x1=28,x2=32,答:当天该消毒液的售价为28元或32元;(3)设利润为W元,W=(x-20)(-2x+80)+20(-2x+80)=-2x2+80x=-2(x-20)2+800,∵24≤x≤32,∴当x=24时,W取得最大值,此时W=-2×(24-20)2+800=768(元),答:售价定为24元时,最大日利润是768元.
(1)当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线C2的函数解析式(不要求写出自变量x的取值范围);(2)在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?(3)当运动员运动到坡顶正上方,且与坡顶距离超过3米时,求b的取值范围.
7.(2021·江西赣州模拟)如图①所示的健身器械为倒蹬机,使用方法为上身不动,腿部向前发力,双腿伸直之后,然后再慢慢回收.图②为示意图,已知DE,DC在初始位置,DE=DC=60 cm,点B,C,G在同一直线上,AB⊥BG,∠A=46°,∠DCG=95°.(1)当DE,DC在初始位置时,求点D到AC的距离;
(2)当双腿伸直后,如图③,点E,D分别从初始位置运动到点E′,D′,假设E′,D′,C三点共线,求此时点E上升的竖直高度.(结果保留整数)(参考数据:sin 41°≈0.66,cs 41°≈0.75,tan 41°≈0.87,cs 44°≈0.72,sin 44°≈0.69,tan 44°≈0.97)
解:(1)如图②中,过点D作DH⊥AC于H.∵∠B=90°,∠A=46°,∴∠ACB=44°,∴∠DCH=180°-∠ACB-∠DCG=41°,在Rt△DCH中,DH=CD·sin 41°=60×0.66≈40(cm),∴点D到AC的距离为40 cm.
(2)如图③中,过点D作DH⊥AC于H.∵DE=DC,DH⊥EC,∴EH=CH=CD·cs 41°=60×0.75≈45(cm),∵CE′=120 cm,EC=90 cm,∴时点E上升的竖直高度=(120-90)·sin 44°≈21(cm).
8.(2021·江西模拟)图①是一个放置在水平桌面上的可调节的手机直播架,忽略部件的粗细,它的正面简化结构图如图②所示.中轴HC垂直于水平桌面.已知B为中轴HC上一点,BC=10 cm.支架AD=AE=26 cm,滑动条EP=DP,且P可在BC之间滑动.当三脚架完全合拢时,点P与点B重合,点D,E与点C重合.圆形补光灯的直径为20 cm,它与中轴HC连接,且能够绕点H前后旋转,当圆形补光灯直立时,补光灯的最高点G与C,B,A,H在同一条直线上.
(1)打开支架,使点P与点C重合,图③是直播架脚部左侧的一部分几何图形,求此时∠DAC的度数;(2)在(1)的条件下,已知点H与桌面MN的距离为34 cm,因直播需要将补光灯绕点H向前旋转35°(图④为此时的左侧面简化图),求此时补光灯的最高点G′与桌面的距离.(结果精确到0.1.参考数据:sin 22.60°≈0.38,sin 12.6°≈0.22,cs 22.6°≈0.92,sin 35°≈0.57,cs 35°≈0.82,tan 35°≈0.70)
(2)过点G′作G′T⊥GH于T.在Rt△THG′中,HG′=10 cm,∠THG′=35°,∴TH=HG′·cs 35°=8.2(cm),∴TC=HC+HT=34+8.2=42.2(cm).∴此时补光灯的最高点G′与桌面的距离为42.2 cm.
2023山西省中考复习数学满分大专题冲刺专题二 代数建模 课件: 这是一份2023山西省中考复习数学满分大专题冲刺专题二 代数建模 课件,共30页。PPT课件主要包含了典例精讲,180-2x,195-2x,200-2x,满分训练,12-x等内容,欢迎下载使用。
2023山西省中考复习数学满分大专题冲刺专题二 代数建模 课件: 这是一份2023山西省中考复习数学满分大专题冲刺专题二 代数建模 课件,共30页。PPT课件主要包含了典例精讲,180-2x,195-2x,200-2x,满分训练,12-x等内容,欢迎下载使用。
2023年九年级中考数学函数建模应用题型实例讲解 课件: 这是一份2023年九年级中考数学函数建模应用题型实例讲解 课件,共60页。PPT课件主要包含了类型1一次函数建模,第1题图,第4题图,第6题图,第7题图,第8题图,类型3二次函数建模,第11题图,第11题解图,第14题图等内容,欢迎下载使用。












