中考函数建模专题课件

这是一份中考函数建模专题课件，共18页。PPT课件主要包含了选择模型，求解模型，检验模型，使用模型，不符合，收集数据，画散点图等内容，欢迎下载使用。

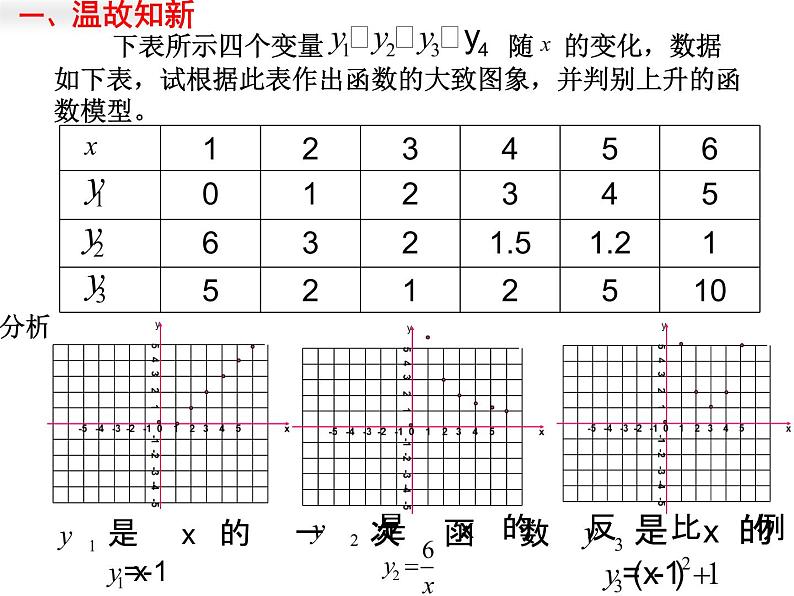
下表所示四个变量 随 的变化，数据如下表，试根据此表作出函数的大致图象，并判别上升的函数模型。
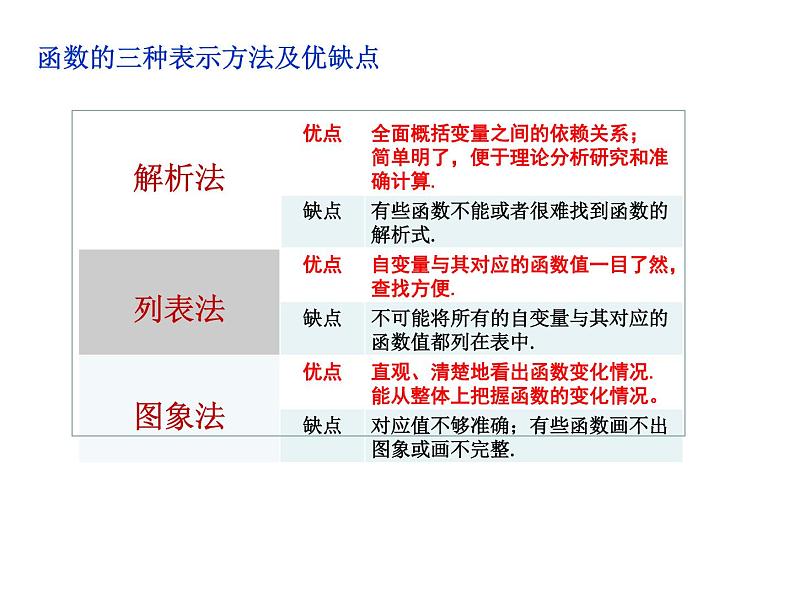
函数的三种表示方法及优缺点
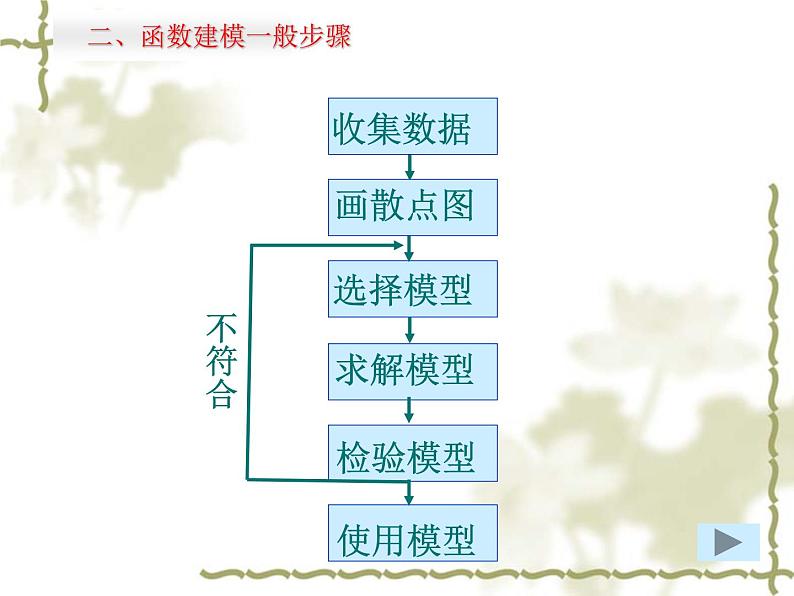
二、函数建模一般步骤
三、例题讲解
例1 如图1，AB是半圆O的直径，弦CD∥AB，点P是AB上一动点，连结CP，DP．已知AB＝10，CD＝8，设PA＝x，PC2＝y．小明利用“几何画板”软件进行观察，测量，得到y随x变化的一组对应值，并在平面直角坐标系中以各对应值为坐标描点（如图2）．（1）请你在图2中连线，观察图象特征并猜想y与x可能满足的函数类别．（2）小明结合图1，发现应用圆、三角形和函数知识能验证（1）中的猜想，请你求出y关于x的函数表达式．
（3）当CP⊥PD时，求x的值．
解：（1）y是x的二次函数
例2 如图1，点C是半圆O的直径AB上一动点（不包括端点），AB＝6cm，过点C作CD⊥AB交半圆于点D，连结AD，过点C作CE∥AD交半圆于点E，连结EB．牛牛想探究在点C运动过程中EC与EB的大小关系．他根据学习函数的经验，记AC＝xcm，EC＝y1cm，EB＝y2cm．请你一起参与探究函数y1、y2随自变量x变化的规律．通过几何画板取点、画图、测量，得出如下几组对应值，并在图2中描出了以各对对应值为坐标的点，画出了不完整图象．
（1）当x＝3时，y1＝　 　．(2)在2中画出函数y2的图象，并结合图象判断函数值y1与y2的大小关系．
由图象得：当0＜x＜2时，y1＜y2，当x＝2时，y1＝y2，当2＜x＜6时，y1＞y2；
（3）由（2）知“AC取某值时，有EC＝EB”．如图3，牛牛连结了OE，尝试通过计算EC，EB的长来验证这一结论，请你完成计算过程．
1．如图（1），在△ABC中，AB＝AC，∠BAC＝90°，边AB上的点D从顶点A出发，向顶点B运动，同时，边BC上的点E从顶点B出发，向顶点C运动，D，E两点运动速度的大小相等，设x＝AD，y＝AE+CD，y关于x的函数图象如图（2），图象过点（0，2），（1）AB的长为 ，（2）图象最低点的横坐标是 　 　．
2 .如图，Rt△ABC，∠C＝90°，CA＝CB＝4 cm，
点P为AB边上的一个动点，点E是CA边的中点，连接PE，设A，P两点间的距离为xcm，P，E两点间的距离为y cm．小安根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小安的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
（说明：补全表格时相关数值保留一位小数）
（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：①写出该函数的一条性质：　 　；②当PE＝2PA时，AP的长度约为 .　 　　
（2）函数图象如图所示：
(3）①该函数有最小值或最大值；或当x＞2时，y随x的增大而增大．
②当PE＝2PA时，观察图象可知：AP的长度约为1.1cm．
3. 如图1，在△ABC中，AE平分∠BAC交BC于E，D是AB边上一动点，连接CD画交AE于点P，连接BP．已知AB＝6cm，设B，D两点间的距离为xcm，B，P两点间的距离为y1cm，A，P两点间的距离为y2cm．小华根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．下面是小华的探究过程，请补充完整（1）按照表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值，如下表：
并在平面直角坐标系xOy中画出了y1的图象，如图2所示：
①请在同一平面直角坐标系中画出函数y2的图象．②表格中空缺的数据约为 　 　．
解：（1）用光滑的曲线连接y2图象现有的点，在图象上，测量出x＝5时，y＝1.35（答案不唯一）；
（2）继续在同一坐标系中，画出所需要的函数图象，并结合函数图象直接写出：当AP＝2BD时，AP长度的近似值约为 　 　cm（结果保留两位小数）（3）小华继续探究，得到：当BP平分∠ABC时，BD的长度是一个确定的值，请直接写出此时BD的长度．
（2）绘制后y1、y2图象如下：
当AP＝2BD时，即y2＝2x，在图象上画出直线y＝2x，该图象与y2的交点即为所求，即图中空心点所示，
空心点的纵坐标为3.88，故答案为3.88（不唯一）；
（3）从表格数据看，当x＝3时，y1＝y2＝3.25，即点D在AB中点时，y1＝y2，即此时点P在AB的中垂线上，则点C在AB的中垂线上，则△ABC为等腰三角形，故当BP平分∠ABC时，此时点P是△ABC的内心，故点D在AB的中点，∴BD＝
总结一下本节课你的收获是什么？
五、总结归纳
1.函数模型的应用实例的基本题型:（1）给定函数模型解决实际问题；（2）建立确定性的函数模型解决问题；（3）建立拟合函数模型解决实际问题。2．数学建模的基本步骤是： 审题
小 结