






2023山西省中考复习数学满分大专题冲刺专题二 代数建模 课件
展开1.(2022适应性)平遥推光漆器作为首批国家级非物质文化遗产深受广大游客的喜爱. 某商店准备购进A,B两种型号的推光漆器,一件A型漆器比一件B型漆器进价贵20元,花500元购进的A型漆器与花400元购进的B型漆器数量相同.(1)求A,B两种型号漆器每件的进价.
经检验,x = 80是原方程的解,且符合实际.x + 20 = 100(元).答:A,B两种型号的漆器每件的进价分别是100元和80元.
(2)该店决定购进A,B两种型号的漆器共60件,其中A型漆器a件.根据销售经验,购进B型漆器的数量不少于A型漆器的2倍.已知A型漆器每件的售价为125元,B型漆器每件的售价为100元.设60件漆器全部售完获利w元,当该店购进A,B两种型号漆器各多少件时,才能使w最大?
(2)根据题意得 w = (125 - 100)a + (100 - 80) (60 - a)= 5a + 1 200 .∵ 60 - a ≥ 2a ,∴ a ≤ 20 .∵5 > 0,∴w随a的增大而增大.∴当a = 20时,w最大,此时B型漆器的件数为60 - 20 = 40(件).答:该商店购进20件A型漆器、40件B型漆器时,w最大.
3.(2022眉山)建设美丽城市,改造老旧小区.某市2019年投入资金1 000万元,2021年投入资金1 440万元,现假定每年投入资金的增长率相同.(1)求该市改造老旧小区投入资金的年平均增长率.
解:(1)设该市改造老旧小区投入资金的年平均增长率为x.依题意得1 000(1 + x)2 = 1 440.解得x1 = 0.2,x2 = -2.2(不合题意,舍去).答:该市改造老旧小区投入资金的年平均增长率为20%.
(2)2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区.
4. 我运动,我健康,我快乐,我成长.周末,甲、乙两名同学相约在同一路段进行长跑训练,两人在起点会合后,甲出发3分钟时,乙出发,结果乙比甲提前2分钟到达终点.两人到达终点即停止,全程匀速.如图,设甲离开起点后经过的时间为x(分),甲离开起点的路程y1 (米)与x(分)之间的函数关系式为y1 = 150x,图象为线段OA;乙离开起点的路程y2(米)与x(分)之间的函数关系用线段BC表示,请根据图象中的信息解决下列问题:(1)图中m的值为 ,n的值为 .
(2)求线段BC对应的函数表达式. (不必写出自变量的取值范围)
(3)直接写出点D的坐标,并解释点D的坐标表示的实际意义.
(3)D(12,1 800).点D的坐标表示的实际意义是甲出发12分钟后,乙在距出发点1 800米的地方追上甲.
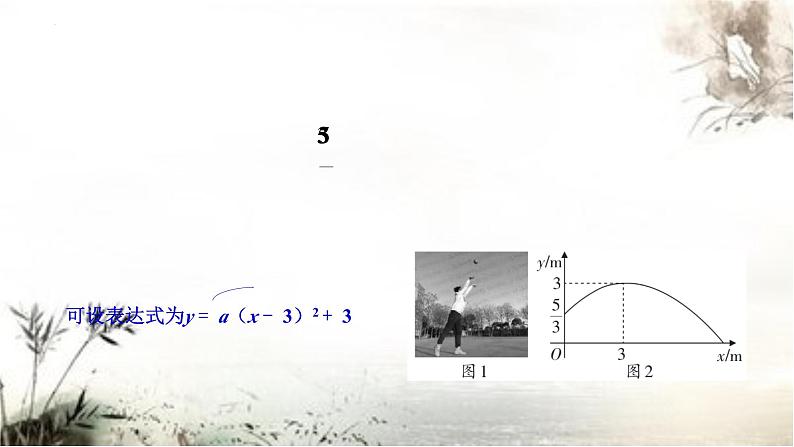
5. 山东新泰香椿畅销全国各地.当地某电商对一款成本为每件30元的香椿商品进行直播销售,如果按每件40元销售,平均每月可卖出600件.通过市场调查发现,每件香椿商品售价每上涨1元,其月销售量将减少10件.已知该电商平均每月的销售利润为12 000元.(1)这种商品每件的售价应为多少元?
方法二,设这种商品每件的售价为a元.根据题意得,(a -30)[600 -(a - 40)× 10]= 12000.解得a1 = 60,a2 = 70.答:这种商品每件的售价为60或70元.
(2)这时电商每月能售出该香椿商品多少件?
(2)600 - 20 × 10 = 400,600 - 30 × 10 = 300.答:这时电商每月能售出该香椿商品400件或300件.
6.(2022重庆)为保障蔬菜基地种植用水,需要修建灌溉水渠.(1)计划修建灌溉水渠600米,甲施工队施工5天后,增加施工人员,每天比原来多修建20米,再施工2天完成任务,求甲施工队增加人员后每天修建灌溉水渠多少米.
解:(1)设甲施工队增加人员后每天修建灌溉水渠x米,则原计划每天修建(x - 20)米.由题意得5(x - 20)+ 2x = 600.解得x = 100.答:甲施工队增加人员后每天修建灌溉水渠100米.
(2)因基地面积扩大,现还需修建另一条灌溉水渠1 800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建360米后,通过技术更新,每天比原来多修建20%,灌溉水渠完工时,两施工队修建的长度恰好相同.求乙施工队原来每天修建灌溉水渠多少米.
思路启迪乙施工队修建360米需要的时间为 天.乙施工队修建(900 - 360)米需要的时间为 天甲施工队修建900米需要的时间为 天
7.如图,某工程队利用互相垂直的两面墙AE,AF,用铁栅栏围成一个长方形场地ABCD,中间再用铁栅栏分割成两个长方形.已知墙AE长为90米,墙AF长为60米,设BC = x米.(1)若铁栅栏总长为180米,则CD长为 米,四边形ABCD的面积为 米.(用含x的代数式直接写出结果)
x(180 - 2x)
(2)若所有铁栅栏采用双层加固(两层铁栅栏间的缝隙忽略不计),为了方便运输货物,CD边上需留出两个宽均为2.5米的缺口.已知铁栅栏总长为390米,求围成的长方形场地的最大面积.
思路启迪单层栅栏长度为 米.CD边上需要的单层栅栏为 米.CD的长为 米.
(2)依题意得2(CD - 5)+ 4x = 390.∴CD = 200 - 2x.设长方形场地ABCD的面积为S,则S = x(-2x + 200)= -2(x - 50)2 + 5 000.∵200 - 2x ≤ 90,x ≤ 60∴55 ≤ x ≤ 60.∴当x = 55时,S 最大 = 4 950(平方米).答:围成的长方形场地的最大面积为4 950平方米.
1. 为了贯彻习近平总书记考察调研山西时关于治水的指示精神,某市扎实推进“两山七河一流域”生态修复工程. 现计划由A,B两个工程队对一条长2 250米的河道进行修复,已知A工程队每天修复河道的长度是B工程队每天修复河道的长度的2倍. 同样修复300米的河道,A工程队比B工程队少用2天.
(1)求A,B两个工程队每天能修复河道的长度分别为多少米.
(2)A,B两个工程队共同施工6天后,B工程队被紧急调走,剩下的修复任务由A工程队完成,且剩下的修复任务要求在5天内完成,请问A工程队每天至少要多修复河道多少米.
(2)设A工程队现在每天要多修复河道y米.根据题意得5(150 + y)≥ 2 250 - 6 ×(150 + 75).解得y ≥ 30 .答:A工程队现在每天至少要多修复河道30米.
2. 裕丰花鸟市场某园艺公司在销售中发现:一款成本为8元/盆的绿植,销售价为20元/盆时,每天可售出100盆.现为增加利润,且尽快减少库存,公司采取降价措施.若销售单价每降价1元,则绿植可多售出20盆,设每盆降价x元.( 0 < x < 12,x为整数)(1)降价后,每盆盈利 元,每天可售出 盆.(2)在满足公司要求的情况下,每盆降价多少元时,每天可盈利1 400元.
(2)设每天销售利润为w元,w =(12 - x)(100 + 20x)= 1 400,解得x1 = 2,x2 = 5.又∵要尽快减少库存,∴x = 5.答:每盆降价5元时,每天可盈利1 400元.
(100 + 20 x)
(3)在满足公司要求的情况下,每盆降价多少元时,可取得最大利润?并求出最大利润.
3. (2022德阳)习近平总书记对实施乡村振兴战略作出重要指示强调:实施乡村振兴战略,是党的十九大作出的重大决策部署,是新时代做好“三农”工作的总抓手.为了发展特色产业,红旗村花费4 000元集中采购了A种树苗500株,B种树苗400株,已知B种树苗单价是A种树苗单价的1.25倍.(1)求A,B两种树苗的单价分别是多少元.
中考数学复习微专题二常考的四大相似模型模型一A字型课件: 这是一份中考数学复习微专题二常考的四大相似模型模型一A字型课件,共7页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。
专题四 阅读理解课件冲刺2023年山西中考数学满分大专题: 这是一份专题四 阅读理解课件冲刺2023年山西中考数学满分大专题,共60页。PPT课件主要包含了类型一代数阅读,一新概念型,二方法型,ACAD或CD,三运算型,n25,类型二几何阅读,∠B∠B,∠C∠C,二操作型等内容,欢迎下载使用。
2023山西省中考复习数学满分大专题冲刺专题二 代数建模 课件: 这是一份2023山西省中考复习数学满分大专题冲刺专题二 代数建模 课件,共30页。PPT课件主要包含了典例精讲,180-2x,195-2x,200-2x,满分训练,12-x等内容,欢迎下载使用。












