


还剩7页未读,
继续阅读
初中数学青岛版九年级上册第3章 对圆的进一步认识3.3 圆周角课文课件ppt
展开
这是一份初中数学青岛版九年级上册第3章 对圆的进一步认识3.3 圆周角课文课件ppt,共13页。PPT课件主要包含了圆周角,类比圆心角探知圆周角,圆周角和圆心角的关系,∵OAOB,∴∠A∠B,∴∠AOC2∠B,你能写出这个命题吗,圆周角定理,思考与巩固等内容,欢迎下载使用。
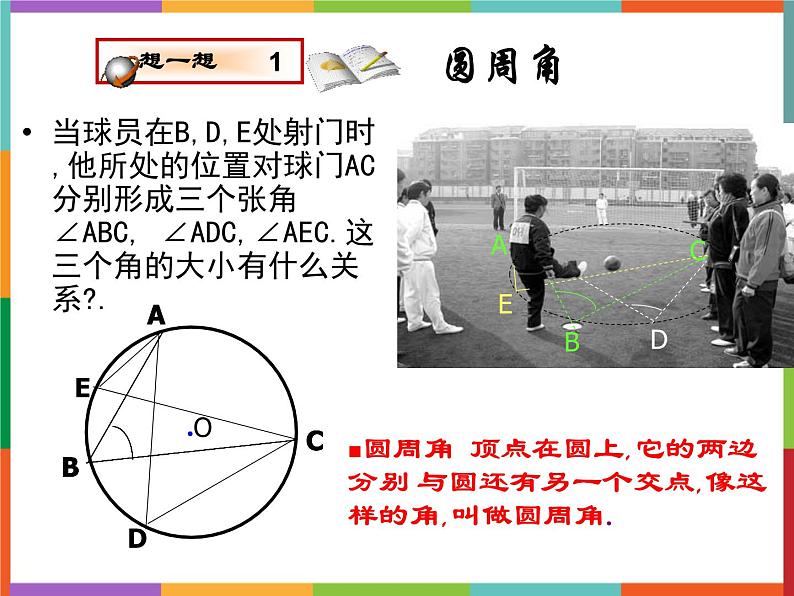
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.
圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.
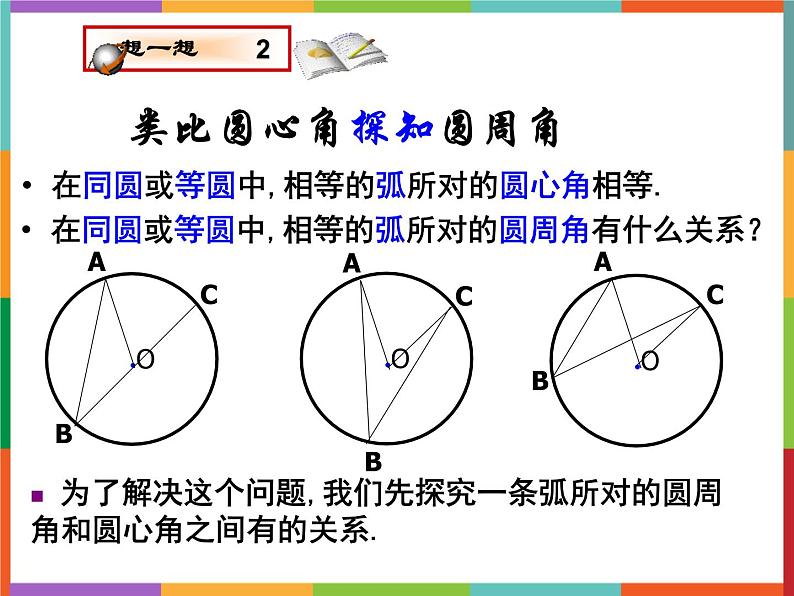
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.
如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?
说说你的想法,并与同伴交流.
教师提示:注意圆心与圆周角的位置关系.
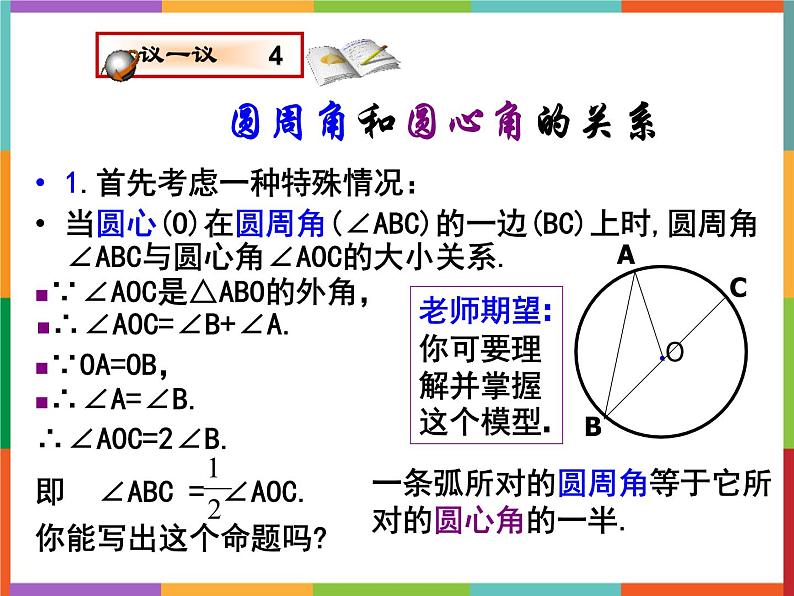
1.首先考虑一种特殊情况:当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
一条弧所对的圆周角等于它所对的圆心角的一半.
老师期望:你可要理解并掌握这个模型.
如果圆心不在圆周角的一边上,结果会怎样?2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否转化为1的情况?
过点B作直径BD.由1可得:
如果圆心不在圆周角的一边上,结果会怎样?3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否也转化为1的情况?
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:
圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.
老师提示:圆周角定理是承上启下的知识点,要予以重视.
1.如图,在⊙O中,∠BOC=50°,求∠A的大小.
2.如图(2),在⊙O中,∠BAC=50°,求∠C的大小.
拓展 化心动为行动
1.如图,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?2.想一想,等圆中也有这样的结论吗?
同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等。
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.
圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.
如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?
说说你的想法,并与同伴交流.
教师提示:注意圆心与圆周角的位置关系.
1.首先考虑一种特殊情况:当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
一条弧所对的圆周角等于它所对的圆心角的一半.
老师期望:你可要理解并掌握这个模型.
如果圆心不在圆周角的一边上,结果会怎样?2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否转化为1的情况?
过点B作直径BD.由1可得:
如果圆心不在圆周角的一边上,结果会怎样?3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否也转化为1的情况?
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:
圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.
老师提示:圆周角定理是承上启下的知识点,要予以重视.
1.如图,在⊙O中,∠BOC=50°,求∠A的大小.
2.如图(2),在⊙O中,∠BAC=50°,求∠C的大小.
拓展 化心动为行动
1.如图,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?2.想一想,等圆中也有这样的结论吗?
同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等。













