




初中数学青岛版(2024)九年级上册第3章 对圆的进一步认识3.3 圆周角获奖教学ppt课件
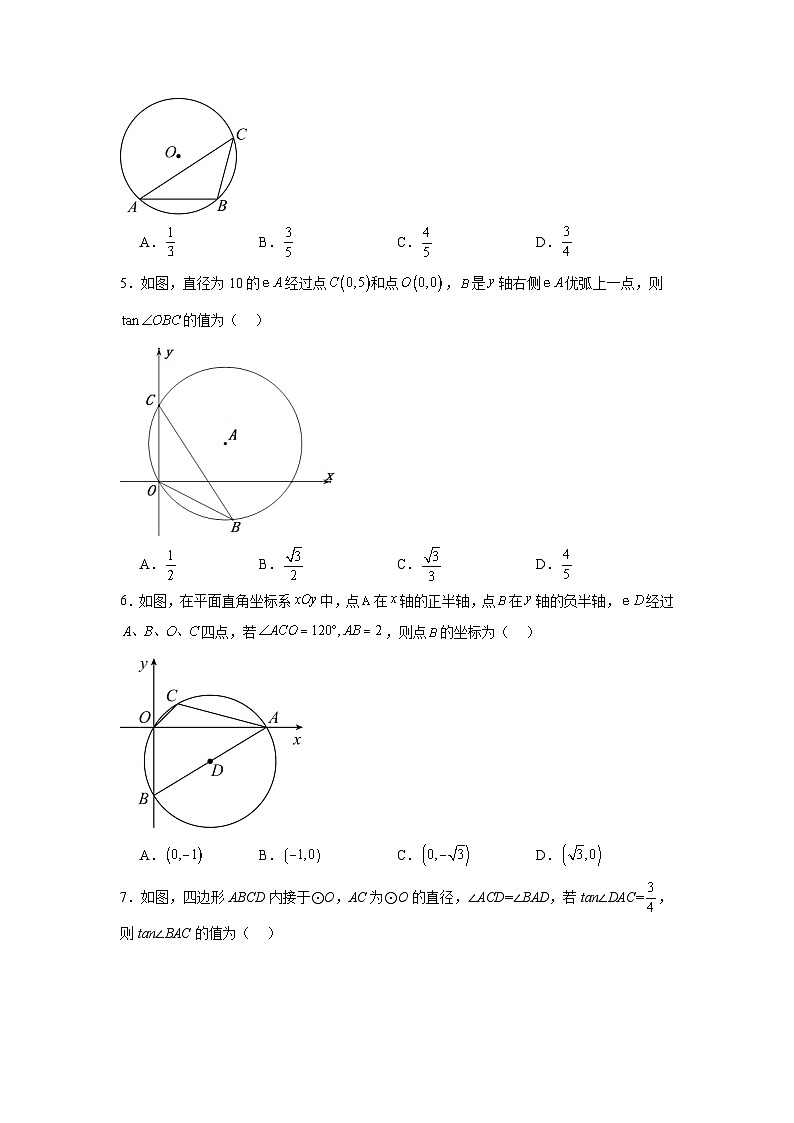
展开3.3圆周角(同步练习)(解析板)一、单选题1.如图,点A,B,C,D在上,,点D是的中点,则的度数是( )A.36 B.40 C.46 D.72【答案】A【分析】连接OD,根据点D是中点求出∠COD,再利用圆周角定理得出结果.【详解】解:连接OD,∵D是的中点,∴∠COD= ,∴∠B= ,故选择A.【点睛】本题考查圆周角定理以及弧和圆心角关系,注意通过弧进行角的转化是解决问题的关键.2.下列说法:(1)等弧所对的圆周角相等;(2)过三点可以作一个圆;(3)平分弦的直径垂直于弦;(4)半圆是一条弧,其中正确的是( )A.(1)(2)(3)(4) B.(1)(2)(3)C.(2)(3)(4) D.(1)(4)【答案】D【分析】利用确定圆的条件、圆的有关性质及定义分别判断后即可确定正确的选项.【详解】解:(1)等弧所对的圆周角相等,正确;(2)过不在同一直线上的三点可以作一个圆,故原命题错误;(3)平分弦(不是直径)的直径垂直于弦,故原命题错误;(4)半圆是一条弧,正确,其中正确的是(1)(4),故选:D.【点睛】考查了确定圆的条件、圆的有关性质及定义,属于圆的基础知识,比较简单,解题的关键是牢记有关性质及定义.3.如图,AB是⊙O的直径,BC是⊙O的弦,先将沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若,则∠BCD的度数是( )A.22.5° B.30° C.45° D.60°【答案】C【分析】连接,,,设,证明,利用三角形内角和定理求出,可得结论;【详解】解:如图,连接,,,设,,,,,,,,∵是直径,,,,,,故选:C.【点睛】本题考查翻折变换,圆周角定理,等腰三角形的判定和性质,三角形内角和定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.4.如图,在半径为5的中,弦,点C是优弧上一点(不与A、B重合),则的值为( )A. B. C. D.【答案】C【分析】此题考查了圆周角定理、勾股定理以及三角函数的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.首先作直径AD,连接BD,由直径所对的圆周角是直角,即可得,然后由勾股定理求得BD的长,继而求得,又由圆周角定理,可得,则可求得答案.【详解】解:作直径AD,连接BD,∴,,∴在中,,∴,∵,∴.故选:C.5.如图,直径为10的经过点和点,是轴右侧优弧上一点,则的值为( )A. B. C. D.【答案】C【分析】首先设与x轴的另一个交点为D,连接CD,根据90°的圆周角所对的弦为直径,即可得到CD是直径,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,可得∠OBC=∠ODC,继而可求出答案.【详解】解:设设与x轴的另一个交点为D,连接CD,∵∠COD=90°,∴CD是直径,即CD=10,∵,∴OC=5,∴OD=,∵∠OBC=∠ODC,∴===.故选C.【点睛】本题考查了圆周角定理,勾股定理,锐角三角函数.注意掌握辅助线的作法及数形结合与转化思想的运用.6.如图,在平面直角坐标系中,点在轴的正半轴,点在轴的负半轴,经过四点,若,则点的坐标为( )A. B. C. D.【答案】A【分析】先利用圆内接四边形的性质得到,再根据圆周角定理得到为的直径,则点为的中点,接着利用含30度角的直角三角形三边的关系得到,即可确定点坐标.【详解】解:∵四边形为圆的内接四边形,,∴,∴,∵,∴为的直径,∴点为的中点,在中,∵,∴,∴,∴点坐标为.故选:A.【点睛】本题主要考查了坐标与图形、圆内接四边形的性质、圆周角定理、含30度角的直角三角形的性质等知识,熟练掌握圆内接四边形的性质和圆周角定理是解题关键.7.如图,四边形ABCD内接于⊙O,AC为⊙O的直径,∠ACD=∠BAD,若tan∠DAC=,则tan∠BAC的值为( )A. B. C. D.【答案】D【分析】延长AD、BC交于点E,由△EDC∽△EBA,推出,求出BE,AB即可解决问题.【详解】解:延长AD、BC交于点E,∴∠BAD=∠2,∵∠1=∠BAD,∴∠1=∠BAD=∠2,∵AC为⊙O的直径,∴∠ADC=,∴AD=DE,AC=CE,∵tan∠DAC=,即=,∴设CD=3k,则AD=DE=4k,AC=CE=5k,AE=8k,∵∠BAE=∠2,∠E公共,∴△EDC∽△EBA,∴,∴EB=,AB=,∴BC=BE-EC=-5k=,∴.故选:D.【点睛】本题考查圆周角定理,相似三角形的判定和性质,解直角三角形等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.8.如图,依次是残破镜子上的三个点,弓形的弦的长为,,则这个镜子的直径长为( )A. B. C. D.【答案】B【分析】本题考查了等腰三角形的性质,圆周角定理,解直角三角形,设点为圆的圆心,连接,过点作于,由等腰三角形的性质可得,,又由圆周角定理可得,得到,最后解直角三角形即可求解,正确作出辅助线是解题的关键.【详解】解:设点为圆的圆心,连接,过点作于,则,∵,∴,,∵,∴,∴,∴,∴镜子的直径长为,故选.9.如图,在中,过点C作,垂足为点D,过点D分别作,,垂足分别为E,F.连接EF交线段CD于点O,若,,则的值为( ).A. B.4 C. D.6【答案】B【分析】由题意易得出,即说明点C,E,D,F四点共圆,得出,从而易证,得出.由题意可求出,即可求出.【详解】解:∵,,∴,∴点C,E,D,F四点共圆,∴,即.又∵,∴,∴,∴.∵,,∴,∴.故选B.【点睛】本题考查相似三角形的判定和性质,四点共圆的知识,圆周角定理.确定点C,E,D,F四点共圆,从而可得出证明的条件是解题关键.10.如图,直角梯形中,,,,过A,B,D三点的分别交,CD于点E,M,且,下列结论:①;②;③的直径为2;④.其中正确的结论是 ( )A.①②③ B.①③④ C.①②④ D.①②③④【答案】C【分析】连接BD,BM,,,DE,由90°角所对的弦为直径,得到BD为圆的直径,再利用直径所对的圆周角为直角,得到为直角,利用三个角为直角的四边形为矩形得到为矩形,利用矩形的对边相等得到,而,等量代换得到,可得出M为的中点,即,故选项①正确;由AB与MC平行且相等,利用一组对边平行且相等的四边形为平行四边形,得到四边形为平行四边形,可得出,而,等量代换得到,由BD为圆的直径,利用直径所对的圆周角为直角得到为直角三角形,由与的长,利用勾股定理求出DE的长,设,则,在直角中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出的长,即为BD的长,确定出圆的直径,即可对于选项③作出判断;在直角中,由M为CD的中点,利用斜边上的中线等于斜边的一半得到与相等,都等于的一半,利用等弦所对的劣弧相等,得到,同时由,得到,等量代换得到,故选项②正确;在直角中,由与的长,利用勾股定理求出的长,即可对于选项④作出判断.【详解】连接BD,BM,,,DE,∵,∴BD为圆的直径,∴,∴,∴四边形矩形,∴,又∵,∴,即;故选项①正确;∵,,∴四边形是平行四边形,∴,又,∴,∵BD是直径,∴,即,又,,根据勾股定理得:,设,,在中,根据勾股定理得:,即,解得:,∴,故选项③错误;在中,M是中点,∴,∴,又∵,∴,∴,故选项②正确;在中,,,根据勾股定理得:;故选项④正确;则正确的选项为:①②④.故选C.【点睛】此题属于圆综合题,考查圆周角定理,圆心角、弦及弧之间的关系,勾股定理,直角三角形斜边上的中线性质,矩形的判定与性质,以及平行四边形的判定与性质,利用了方程的思想,熟练掌握性质及定理是解本题的关键.二、填空题11.如图,在中,圆心角,那么圆周角 .【答案】/度【分析】根据在同圆或等圆中,同弧所对的圆周角等于圆心角的一半,可得答案.【详解】解:由题意得:.故答案为:12.已知的半径为4,弦长为 ,则弦所对的圆周角的度数为 °.【答案】或【分析】本题考查的是圆周角定理及垂径定理,圆内接四边形的性质,解题的关键是先根据题意画出图形,连接、,过作,由垂径定理和勾股定理可求出的长,可求出的度数,由圆周角定理及圆内接四边形的性质即可求出答案.【详解】解:如图所示,连接、,过作,则,,,,,则,,,在上取点,连接、,在优弧上取点,连接、,,∴.故答案为:或.13.如图,等边△ABC内接于⊙O,AD是直径,则∠CBD= °.【答案】30°.【详解】解:∵△ABC是等边三角形,∴∠ABC=∠C=∠BAC =60°,根据圆周角定理得:∠D=∠C=60°,∵AD为直径,∴∠ABD=90°,∴∠BAD=30°∴∠CAD=∠BAC-∠BAD=90°-60°=30°∴∠CBD=∠CAD=30°.故答案为:30°14.如图,为锐角的外接圆,点在上,交于点,且满足,连接,设.(1)则 (用含的代数式表示)(2)若,,则 .【答案】 ; ;【分析】(1)根据,,代入求解即可得到答案;(2)根据及(1)可得,结合,且,再利用相似三角形的判定与性质即可得到答案;【详解】(1)解:∵,,,∴,故答空1答案为:;(2)解:∵,∴,∵,,,∴,∵,∴,∵, ∴,∴,,连接,∵,∴,∴,∵,∴,∵,∴,∴,即,变形得:,设,则有。解得,(不符合题意舍去),故答案为:;【点睛】本题主要考查了圆周角定理,平行线的性质,三角形内角和定理,相似三角形判定与性质解题的关键是根据圆周角定理,三角形内角和定理,平行线的性质得到等角从而得到三角形相似.15.如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O直径,AD=8,那么AB的长为 .【答案】4【详解】∵AB=BC,∠ABC=120°,∴∠C=,又∵∠D=∠C,∴∠D=30°,∵AD是⊙O直径,∴∠ABD=90°,∴AB=AD=4.故答案为:.三、解答题16.如图,直线,分别交于,,,四点,,相交于点.若的度数是,的度数是,则,你认为正确吗?请说明理由.【答案】正确,理由见解析.【分析】如图,连接,,,,.由圆周角定理得和.则有.【详解】如图,连接,,,,.∵和分别是所对的圆周角和圆心角,∴,和分别是所对的圆周角和圆心角,∴.∴.【点睛】本题考查圆周角定理,解题的关键是掌握圆周角定理.17.如图,的弦、的延长线相交于点,,的度数为.求、的度数. 【答案】,【分析】本题考查圆周角定理,三角形的外角的性质等知识,先根据同弧所对的圆周角是圆心角的一半,得,,再结合三角形的外角的性质,得,即可作答.解题的关键是熟练掌握圆周角定理.【详解】解:如图:在中, ∵,,∴,∵的度数为.∴,∵,∴.18.如图,为的直径,,为上的点,.若,求的度数.【答案】【分析】连接,,由圆周角定理得出,结合求出的度数,再利用圆周角定理即可求出的度数.【详解】连接,,如图所示:∵,∴,∵,∴,∴,∴【点睛】本题考查了圆周角定理以及圆心角、弧、弦的关系,熟练掌握圆周角定理,利用等弧对的圆心角相等求出的度数是解题关键.19.如图所示,AB为的直径,点C为的中点,点M为OB的中点,连接CM并延长交于点D,若,求CD的长.【答案】【分析】方法1,求弦长,可以利用垂径定理,即过点O作于点H,利用已知条件求出CH的长.方法2,依据直径所对的圆周角是直角构造以CD为边的直角三角形,在该直角三角形中直接求出CD的长.【详解】方法1 如图所示,过点O作于点H,连接OC,则.点M为OB的中点,,.点C为的中点,.在中,.,即,,.方法2 如图所示,作直径CE,连接DE.点M为OB的中点,,.CE是的直径,,点C为的中点,.在中,.,即,.【点睛】本题考查垂径定理的应用、勾股定理的应用、圆周角的性质,关键是根据题意能分析出是利用垂径定理来解答,难点是分析作出辅助线的方法和灵魂运用勾股定理进行计算.20.如图,四边形为菱形,对角线和BD交于点,是的外接圆,与BD交于点,连接. (1)若,的半径为,求的长;(2)当时,探究与的位置关系,并说明理由.【答案】(1)(2)与相切,见解析【分析】(1)连接,,根据菱形的性质得出,根据圆周角定理得出,进而根据弧长公式即可求解;(2)根据菱形的性质证明是的直径,解法一: 连接CF,,设,是的垂直平分线,证明是等边三角形,得出,则,即可得证;解法二:连接CF,,证明,得出,则,得出是等边三角形,进而同解法一,即可得证.【详解】(1)解:连接,, 菱形,, , (2)解:在菱形中,.,,., , , ,是的直径. 解法一: 连接CF,,设, , , 在菱形中, ,, , , . , 是的垂直平分线 , , , 是等边三角形, , . , ,,, , 是的半径, 与相切. 解法二:连接CF,, 是的直径. , ,在菱形中,,, ,, ,, . . ,∴, , , , , , . , 是等边三角形, , , , , , 是的半径, 与相切.【点睛】本题考查了圆周角定理,求弧长,等边三角形的性质与判定,正切的定义,相似三角形的性质与判定,切线的判定,熟练掌握以上知识是解题的关键.
青岛版(2024)九年级上册3.3 圆周角精品教学课件ppt: 这是一份青岛版(2024)九年级上册<a href="/sx/tb_c75360_t3/?tag_id=26" target="_blank">3.3 圆周角精品教学课件ppt</a>,共21页。
数学九年级上册3.2 确定圆的条件完整版教学ppt课件: 这是一份数学九年级上册<a href="/sx/tb_c75359_t3/?tag_id=26" target="_blank">3.2 确定圆的条件完整版教学ppt课件</a>,文件包含32确定圆的条件同步练习原卷版docx、32确定圆的条件同步练习解析版docx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
九年级上册3.1 圆的对称性完整版教学课件ppt: 这是一份九年级上册<a href="/sx/tb_c75358_t3/?tag_id=26" target="_blank">3.1 圆的对称性完整版教学课件ppt</a>,文件包含31圆的对称性同步练习原卷版docx、31圆的对称性同步练习解析版docx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。













