





2021学年4.1 整式课前预习ppt课件
展开1.理解多项式、整式的概念.
2.会确定一个多项式的项数和次数.
问题1:什么叫单项式?
表示数字与字母、字母与字母的积的式子叫做单项式,单独的一个数或一个字母也是单项式.
问题2:怎么确定一个单项式的系数和次数?
单项式中的数字因数称为这个单项式的系数. 一个单项式中,所有字母的指数的和叫做这个单项式的次数.
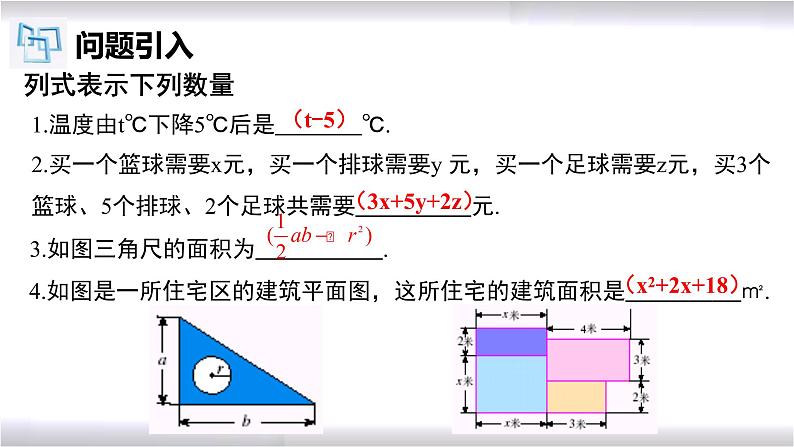
1.温度由t℃下降5℃后是 ℃.
2.买一个篮球需要x元,买一个排球需要y 元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需要 元.
3.如图三角尺的面积为 .
4.如图是一所住宅区的建筑平面图,这所住宅的建筑面积是 ㎡.
它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
上述几个式子都是两个或者多个单项式相加的形式.
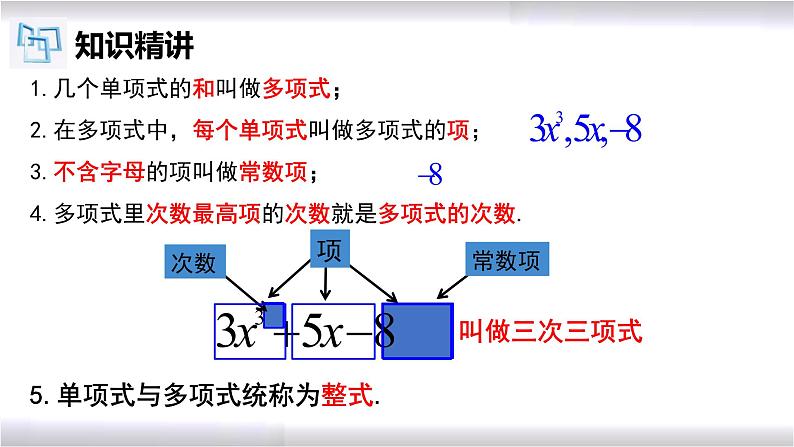
1.几个单项式的和叫做多项式;2.在多项式中,每个单项式叫做多项式的项;3.不含字母的项叫做常数项;4.多项式里次数最高项的次数就是多项式的次数.
5.单项式与多项式统称为整式.
例1:下列整式中哪些是多项式?是多项式的指出其项和次数:
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
1.多项式x2+y-z是单项式___,___,___的和,它是___次___项式.
2.多项式3m3-2m-5+m2的常数项是____,二次项是_____,一次项的系数是_____.
3.一个多项式的次数是3,则这个多项式的各项次数( ) A.都等于3 B. 都小于3 C.都不小于3 D.都不大于3
例2:已知-5xm+104xm+1-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,所以m=4.
【点睛】解题的关键是弄清多项式次数是多项式中次数最高的项的次数.然后根据题意,列出方程,求出m的值.
【分析】该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
所以该多项式为-5x4+104x5-4x4y2.
若关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,求m、n的值.
【分析】关于x的多项式m,n当作已知常数看待,属于系数部分;多项式不含哪一项,则哪一项的系数为0.
解:多项式的二次项是-mx2;一次项是(n-1)x因为不含二次项和一次项所以二次项系数和一次项系数都为0,可得m=0,n-1=0,所以n=1.
一个花坛的形状如图所示,它的两端是半径相等的半圆,求:(1)花坛的周长L;(2)花坛的面积S.
解:(1) L=2a+2πr
(2) 花坛的面积是一个长方形的面积与两个半圆的面积 之和,即S=2ar+ πr2
1.下列式子中,哪些是单项式?哪些是多项式?哪些是整式? 3x,2x-1, ,-ab,-5, -1,3m-4n+m2n. 2.判断正误: (1)多项式- x2y+2x2-y的次数2.( ) (2)多项式 -a+3a2的一次项系数是1.( ) (3)-x-y-z是三次三项式.( )
3.一个关于x的二次三项式的二次项系数为4,一次项系数为1,常数项为7,则这个二次三项式为_____.
解:由题意得2+m+2=6,所以m=2.
又因为3n+4-m+1=6,即3n+3=6,所以n=1.
7.某公园的门票价格是:成人10元/张;学生5元/张. (1)一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?
解:(1)该旅游团应付的门票费是(10x+5y)元. (2)把x=37,y=15代入代数式,得 10x+5y =10×37+5×15 =445. 因此,他们应付445元门票费
初中数学人教版七年级上册2.1 整式教学演示课件ppt: 这是一份初中数学人教版七年级上册2.1 整式教学演示课件ppt,文件包含部编八年级上册语文第六单元教材知识点考点梳理pptx、部编八年级上册语文第六单元教材知识点考点梳理教案docx、部编八年级上册语文第六单元教材知识点考点梳理验收卷原卷版docx、部编八年级上册语文第六单元教材知识点考点梳理验收卷解析版docx等4份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
初中冀教版第四章 整式的加减4.1 整式集体备课课件ppt: 这是一份初中冀教版第四章 整式的加减4.1 整式集体备课课件ppt,共28页。PPT课件主要包含了课堂讲解,课时流程,逐点导讲练,课堂小结,作业提升,知识点,多项式,①③⑤,多项式的项与次数,②④⑥等内容,欢迎下载使用。
初中冀教版4.1 整式习题课件ppt: 这是一份初中冀教版4.1 整式习题课件ppt













