初中数学1、探寻神秘的幻方图文课件ppt

这是一份初中数学1、探寻神秘的幻方图文课件ppt，共33页。PPT课件主要包含了魔术与数学，探寻神奇的幻方，学习目标，幻方的概念，幻方的分类，练习1慧眼识真，探究一幻方的本质，独立思考，探究二幻方的本质，探究幻方本质等内容，欢迎下载使用。

1、通过小组合作，能完成简单的三阶幻方，并根据幻方的性质归纳幻方的定义。2、根据学习有理数的运算和字母表示数的经验，能总结出三阶幻方数字间的规律以及本质特征。3、通过学习巴舍法制作幻方的方法，会制作简单的三阶幻方，体会幻方之间的联系。
公元前三千多年，有条洛河经常发大水，皇帝夏禹带领百姓去治理洛河，这时，从水中浮起一只大乌龟，背上有奇特的图案.
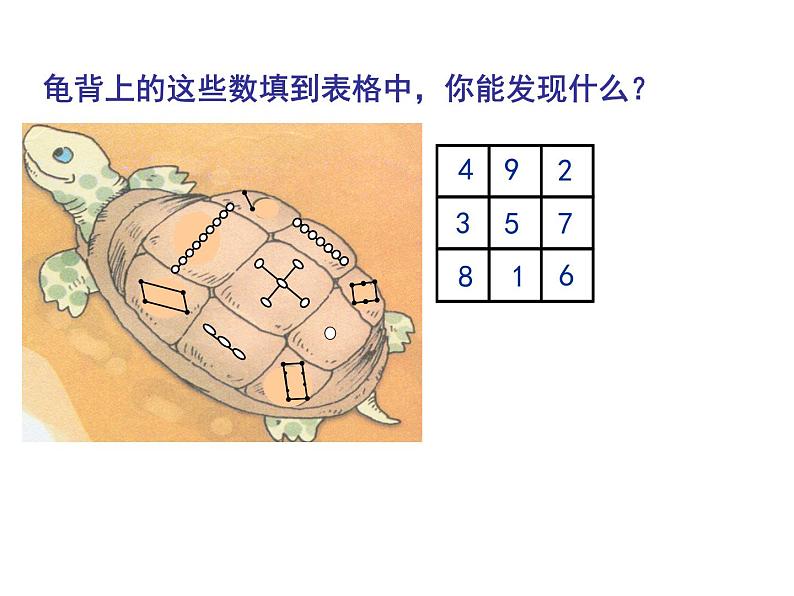
龟背上的这些数填到表格中，你能发现什么？
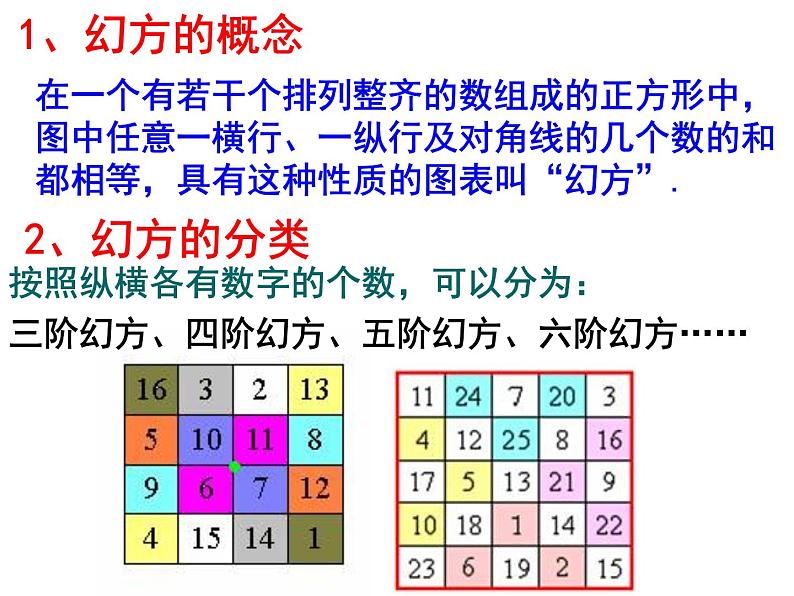
在一个有若干个排列整齐的数组成的正方形中，图中任意一横行、一纵行及对角线的几个数的和都相等，具有这种性质的图表叫“幻方”.
按照纵横各有数字的个数，可以分为：三阶幻方、四阶幻方、五阶幻方、六阶幻方……
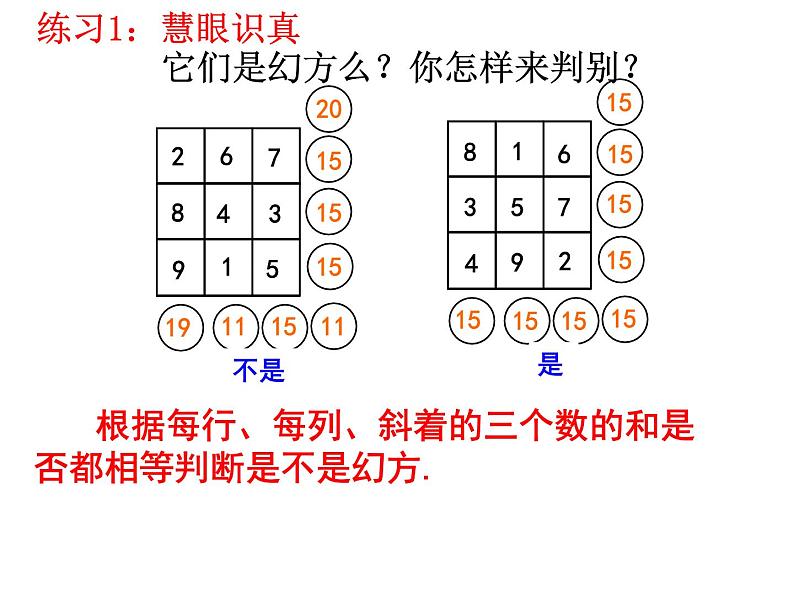
它们是幻方么？你怎样来判别？
根据每行、每列、斜着的三个数的和是否都相等判断是不是幻方.
小组合作将1-9这些数填到表格中，使得每一行，每一列，每一条对角线的三个数字和都是15
问题1：观察这几个数字，你还发现哪些规律？
问题2、你能否改变上述幻方中数字的位置，使它们仍然满足你发现的那些相等关系？
问题3、如果中间的数字用x来表示的话，其他的数字应如何用字母表示？
三阶幻方有技巧,3数斜着先排好,上下左右要交换,然后各自归位了!
如何将1~9这九个数填入九宫格里，使每行、每列及两条对角线上三个数的和都相等？
九子斜列 上下对易左右相更 思维挺出
请你先按规律填空，再将下面三组数分别填入3×3的方格中，使得每行、每列、每条对角线上的三个数之和相等。（1）- 4，- 3，-2，-1，0 ，1 ，2 ，3 ，4.（2） 2 ，4 ，6 ，8 ，10 ，12 ，14，16，18.（3） 3，5， ，9， ，13，15， ， .
想一想：各组的9个数与原来9个数有什么关系？这9个数可以由原来9个数怎么变过来？
（1）幻方中每一个数加、减同一个数字，所得 方格仍是幻方.（2）幻方中每一个数同时扩大或缩小相同的倍数，所得方格仍是幻方.（3）幻方中每一个数先扩大相同的倍数，再同时增加另一个数所得方格仍是幻方.
请各组再列举出九个数，将它们填到3×3的方格中，使得每行、每列、每条对角线上的三个数之和相等.
1：通过本节课的学习，你有那些收获？
（1）（三阶）幻方的概念.（2）幻方的特点.（3）能形成幻方的数据的特点和填入方格的方法.
2：对于本节课，你还想对老师提出什么问题？
1.在下列各图的空格里，填上合适的数，使横行、 竖列及两条对角线上三个数的和都相等.
2.将4、5、6、10、11、12、16、17、18这九个数填入方格里，使之成为幻方.
1.自行选取一组数构造一个三阶幻方,使得每一行、每一列和对角线上的三数之和都等于60.*2.用25个数构造一个五阶幻方.*3.本课时给出的数，从小到大排列，好像都是等距的,不“等距”的9个数能否构成三阶幻方呢？
陕西历史博物馆二楼展厅陈列着一块刻着印度 —— 阿拉伯数码的铁板，这是 1957 年在西安东郊元代安西王府遗址出土的。经专家鉴定，它是一个六阶幻方。
这个幻方铁板是我国数学史上应用阿拉伯数字的最早实物资料，也是元代西安接受阿拉伯文化影响的具体体现。 笔者对这个幻方进行了仔细研究，发现这个六阶幻方不是普通的幻方，它还具有两个独特的性质。
第一，该幻方还是一个二次幻方,幻方中第一行和第六行中六个数的平方和也相等： 282+42+32+312+352+102=3095 272+332+342+62+22+92=3095 第一列和第六列中六个数的平方和也相等： 282+362+72+82+52+272=2947 102+12+302+292+322+92=2947 而一般的幻方根本不具有这个特性.
第二，这个幻方去掉最外面一层，中间剩下的部分仍然是一个四阶幻方。这个四阶幻方由 11 到 26 这 16 个数组成，其每行，每列及两条对角线上的 4 个数之和都是 74 。更为奇特的是，这个4阶幻方还是一个完美幻方。即各条泛对角线上的4个数之和也都是 74 。
百子回归碑是一幅十阶幻方，中央四数连读即“ 1999 · 12 · 20 ”，标示澳门回归日。百子回归碑是一部百年澳门简史，可查阅四百年来澳门沧桑巨变的重大历史事件以及有关史地、人文资料等。如中间两列上部（系十九世纪）：“ 1887 ”年《中葡条约》正式签署，从此成为葡人上百年（距今 100 余 13 年）“永久管理澳门”的法律依据。又如中间两列下部（系二十世纪）：“ 49 ”年中华人民公和国成立，从此中国人民站起来了；“ 97 ”年香港回归祖国。
1977年，美国发射了旅行者1号和2号宇宙飞船，试图与“外星人”建立联系。如何使地外智慧生命理解地球人的意思，这是个很困难的事情，世界各国的人们纷纷献计献策，美国宇航局采纳了其中一些。最后飞船上携带有两件与数学有关的东西，一个是勾股数，另一个是一个4阶幻方，这个幻方，是耆那幻方(Jaina Square) 。
《射雕英雄传》第29和31回　
（瑛姑）双手捧头，苦苦思索，过了一会，忽然抬起头来，脸有喜色，道：“你的算法自然精我百倍，可是我问你：将一至九这九个数字排成三列，不论纵横斜角，每三字相加都是十五，如何排法？”黄蓉心想：“我爹爹经营桃花岛，五行生克之变，何等精奥？这九宫之法是桃花岛阵图的根基，岂有不知之理？”当下低声诵道：“九宫之义，法以灵龟，二四为肩，六八为足，左三右七，戴九履一，五居中央。”边说边画，在沙上画了一个九宫之图。那女子面如死灰。