2020-2021学年25.2 平行线分线段成比例教学ppt课件

这是一份2020-2021学年25.2 平行线分线段成比例教学ppt课件，共14页。PPT课件主要包含了DEBF，∵DEBC，∵DFAC等内容，欢迎下载使用。

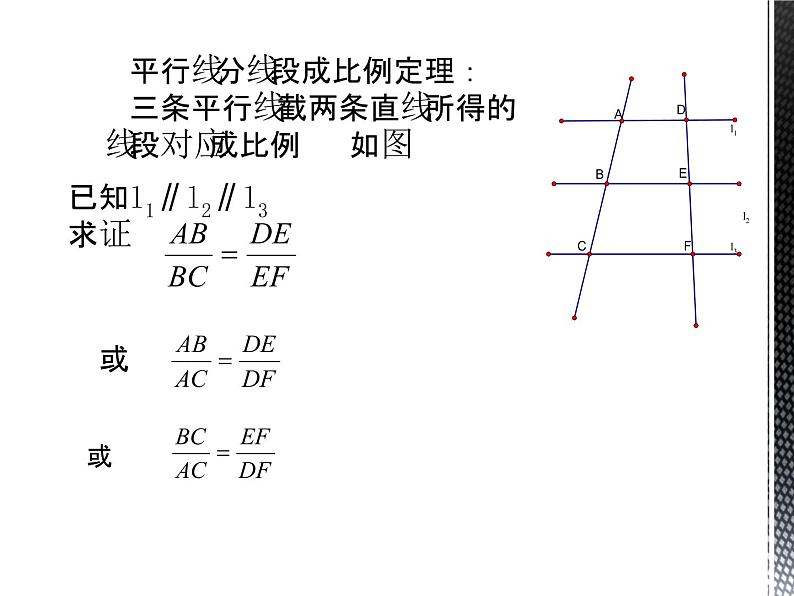
平行线分线段成比例定理：三条平行线截两条直线所得的线段对应成比例 如图
已知l1∥l2∥l3 求证
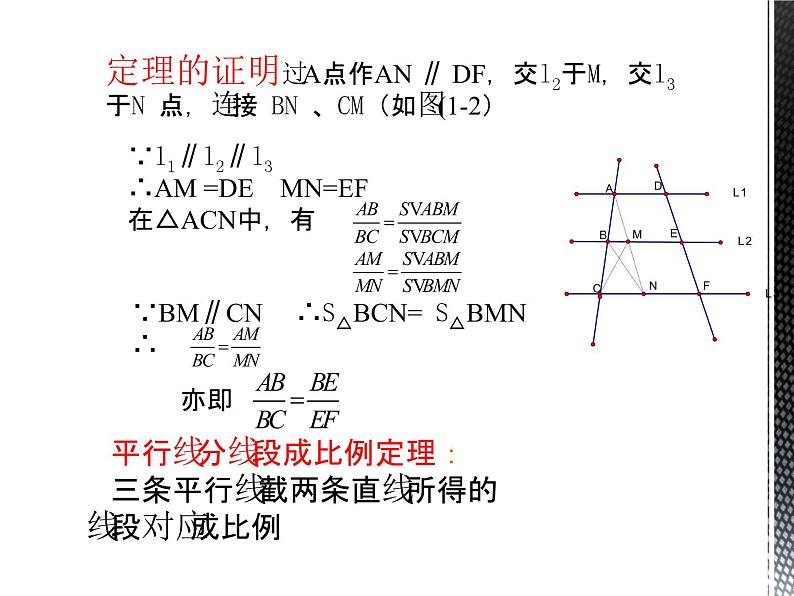
定理的证明过A点作AN ∥ DF，交l2于M，交l3于N 点，连接 BN 、CM（如图(1-2）
∵l1∥l2∥l3∴AM =DE MN=EF在△ACN中，有
∵BM∥CN ∴S△BCN= S△BMN∴
平行线分线段成比例定理：三条平行线截两条直线所得的线段对应成比例
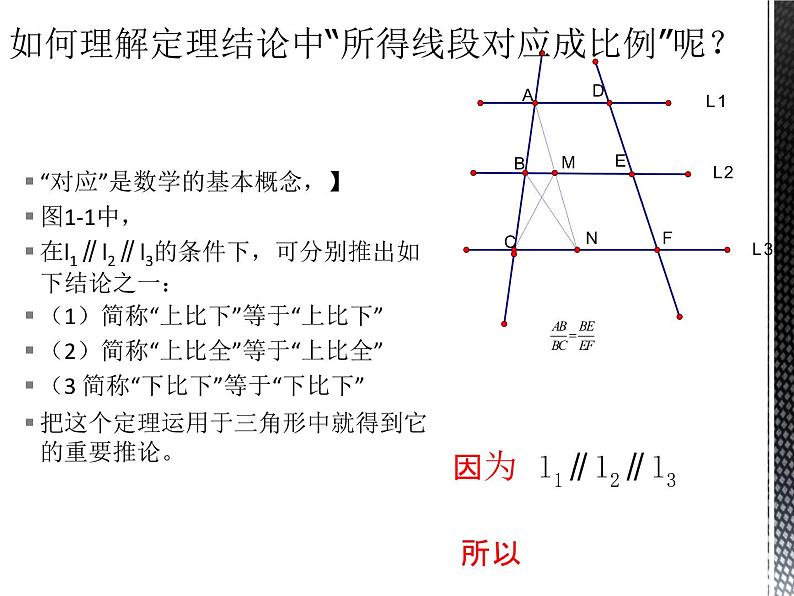
“对应”是数学的基本概念，】图1-1中，在l1∥l2∥l3的条件下，可分别推出如下结论之一：（1）简称“上比下”等于“上比下”（2）简称“上比全”等于“上比全”（3 简称“下比下”等于“下比下”把这个定理运用于三角形中就得到它的重要推论。
因为 l1∥l2∥l3 所以
如何理解定理结论中“所得线段对应成比例”呢？
平行线分线段成比例定理
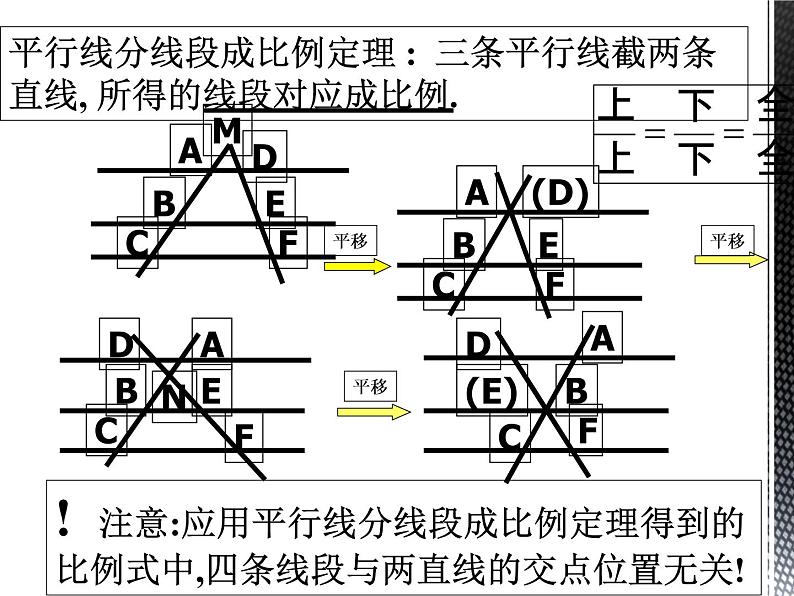
三条平行线截两条直线,所得的线段对应成比例.
! 注意:应用平行线分线段成比例定理得到的比例式中,四条线段与两直线的交点位置无关!
平行线分线段成比例定理 : 三条平行线截两条 直线, 所得的线段对应成比例.
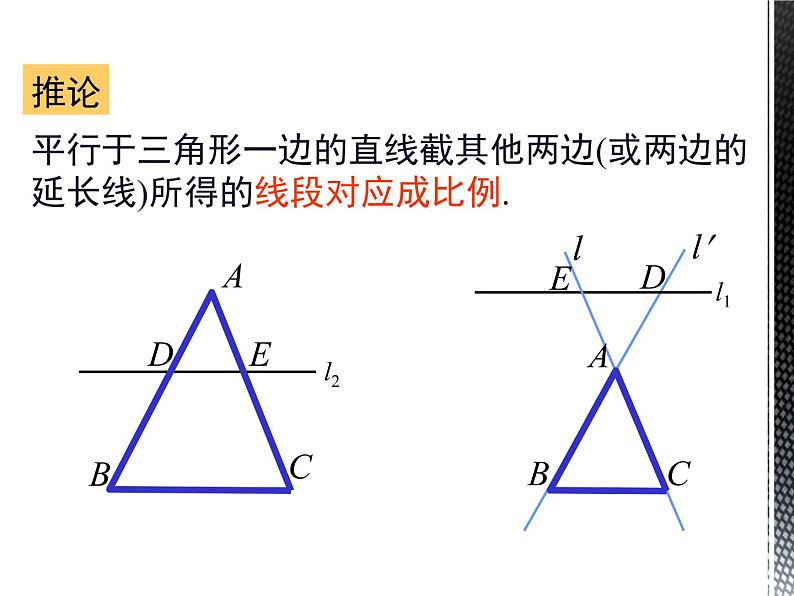
平行于三角形一边的直线截其他两边(或两边的延长线)所得的线段对应成比例.
平行线分线段成比例定理与平行线等分线段定理有何联系？
结论：后者是前者的一种特殊情况！
用平行于三角形一边且和其他两边相交的直线截三角形,所截得的三角形的三边与原三角形的三边对应成比例.
已知:如图,DE//BC,DE分别交AB、AC于点D、E
例 1 如图,△ABC中,DF//AC,DE//BC,AE=4,EC=2, BC=8.求BF和CF的长.
分析:运用平行线分线段成比例定理的推论分别列出比例式求解.
例2 如图,△ABC中,DE//BC,EF//CD. 求证:AD是AB和AF的比例中项.
分析: 分别在△ABC及△ADC中利用平行线分线段成比例定理的推论
∴AD2=ABAF,即AD是AB和AF的比例中项
1、已知AB、CD为梯形ABCD的底，对角线AC、BD的交点为O，且AB=8，CD=6,BD=15，求OB、OD的长。
3、如图，梯形ABCD中，点E、F分别在AB、CD上，EF∥AD，假设EF作上下平行移动，