广东省汕头市龙湖实验中学2022-2023学年九年级上学期开学考试数学试卷（含答案）

这是一份广东省汕头市龙湖实验中学2022-2023学年九年级上学期开学考试数学试卷（含答案），共24页。

2022-2023学年广东省汕头市龙湖实验中学九年级（上）开学
数学试卷（含答案解析）
一.选择题（本题共10小题，每小题3分，共30分）
1．（3分）下列方程是关于x的一元二次方程的是（　　）
A．x+2y＝1 B．x2+x﹣1＝x2 C． D．x2﹣5x＝0
2．（3分）以下列长度的线段为边，不能构成直角三角形的是（　　）
A．2、3、4 B．1、1、 C．3、4、5 D．5、12、13
3．（3分）下列根式中属最简二次根式的是（　　）
A． B． C． D．
4．（3分）下列计算正确的是（　　）
A． B． C． D．
5．（3分）一组数据1，1，3，2，2，1的众数是（　　）
A．3 B．1.5 C．2 D．1
6．（3分）菱形ABCD的两条对角线AC＝8cm，BD＝6cm，那么菱形的边长是（　　）
A．6cm B．5cm C．4cm D．8cm
7．（3分）甲、乙、丙、丁四位优秀短跑选手，近期的10次百米测试平均成绩都是10.3秒，但他们成绩的方差分别是0.020、0.019、0.021、0.022（单位：秒2）．则这四人中发挥最稳定的是（　　）
A．甲 B．乙 C．丙 D．丁
8．（3分）对于一次函数y＝x+6，下列结论错误的是（　　）
A．函数值随自变量增大而增大
B．函数图象与x轴正方向成45°角
C．函数图象不经过第四象限
D．函数图象与x轴交点坐标是（0，6）
9．（3分）三角形的三边长为a，b，c，且满足（a+b）2＝c2+2ab，则这个三角形是（　　）
A．等边三角形 B．钝角三角形 C．直角三角形 D．锐角三角形
10．（3分）如图，已知直线l：y＝x，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2；…；按此作法继续下去，则点B2020的坐标为（　　）

A．（2020，2020） B．（4040，4040）
C．（42020•，42020） D．（22020•，22020）
二.填空题（本大题共7小题，每小题4分，共28分）
11．（4分）计算：＝　 　．
12．（4分）已知三角形三边长分别是6，8，10，则此三角形的面积为 　 　．
13．（4分）如图，△ABC中，三条中位线围成的△DEF的周长是15cm，则△ABC的周长是 　 　cm．

14．（4分）若y＝（m+1）x|m|+3是关于x的一次函数，则m＝　 　．
15．（4分）一次函数y＝kx+b与y＝2x+1平行，且经过点（﹣3，4），则表达式为：　 　．
16．（4分）若x＝3是关于x的一元二次方程x2﹣mx﹣3＝0的一个解，则m的值是　 　．
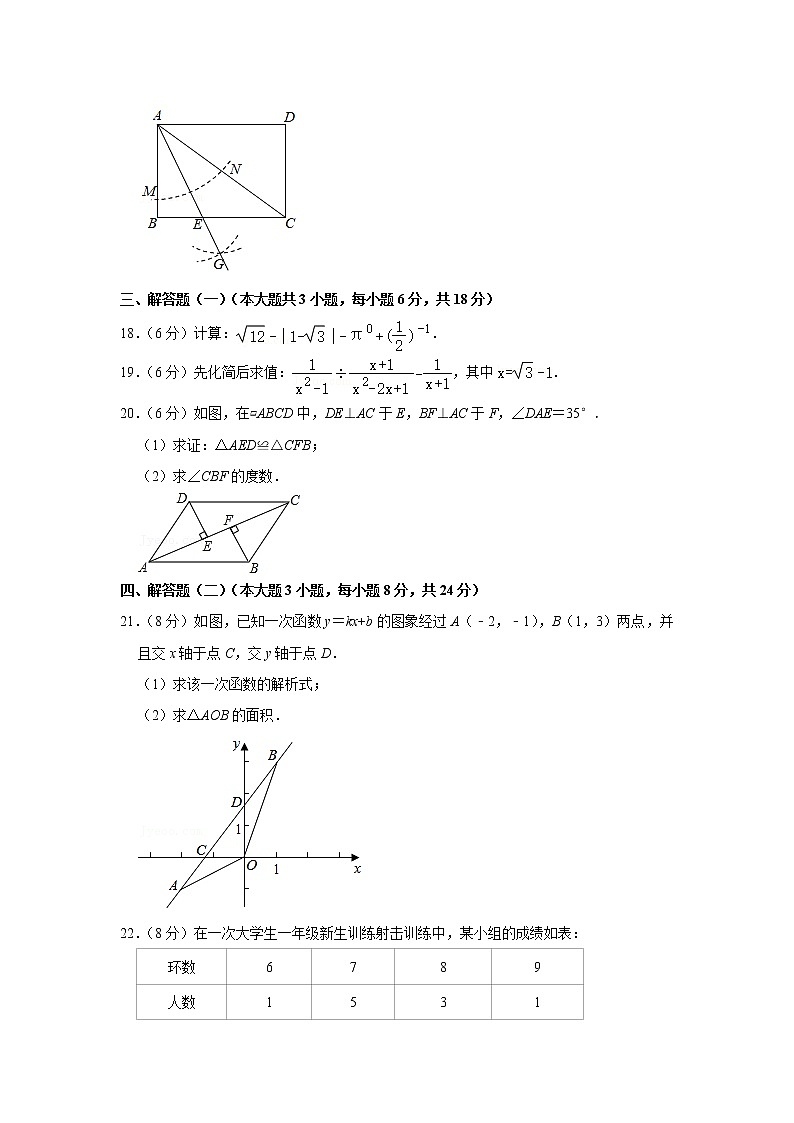
17．（4分）如图，在矩形ABCD中，AB＝6，AD＝8，以A为圆心，任意长为半径画弧交AB，AC于M，N，再分别以M，N为圆心，大于MN为半径画弧，两弧交于点G，连接AG，交边BC于E，则△AEC的周长为　 　．

三、解答题（一）（本大题共3小题，每小题6分，共18分）
18．（6分）计算：．
19．（6分）先化简后求值：，其中．
20．（6分）如图，在▱ABCD中，DE⊥AC于E，BF⊥AC于F，∠DAE＝35°．
（1）求证：△AED≌△CFB；
（2）求∠CBF的度数．

四、解答题（二）（本大题3小题，每小题8分，共24分）
21．（8分）如图，已知一次函数y＝kx+b的图象经过A（﹣2，﹣1），B（1，3）两点，并且交x轴于点C，交y轴于点D．
（1）求该一次函数的解析式；
（2）求△AOB的面积．

22．（8分）在一次大学生一年级新生训练射击训练中，某小组的成绩如表：
环数
6
7
8
9
人数
1
5
3
1
（1）该小组射击数据的众数是 　 　，中位数是 　 　；
（2）求该小组的平均成绩；
（3）若8环（含8环）以上为优秀射手，在1200名新生中有多少人可以评为优秀射手？
23．（8分）某商场计划购进A，B两种新型节能台灯共100盏，这两种台灯的进价、售价如表所示：
类型价格
进价（元/盏）
售价（元/盏）
A型
30
45
B型
50
70
（1）若商场预计进货款为3500元，则这两种台灯各购进多少盏？
（2）若商场规定B型台灯的进货数量不超过A型台灯数量的3倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？
五、解答题（三）（本大题2小题，每小题10分，共20分）
24．（10分）如图，直线AB为y＝kx+6，D（8，0），点O关于直线AB的对称点C在直线AD上．
（1）求直线AD的解析式．
（2）求点C的坐标．
（3）若OC交AB于点E，在线段AD上是否存在一点F，使△ABC与△AEF的面积相等？若存在求出F点坐标，若不存在，请说明理由．

25．（10分）阅读理解：在平面直角坐标系中，任意两点A（x1，y1），B（x2，y2），则①AB两点的距离＝；②线段AB的中点坐标为（，）．
解决问题：
如图，平行四边形ABCD中，点B在x轴负半轴上，点D在第一象限，A，C两点的坐标分别为（0，4），（3，0），边AD的长为6．
（1）若点P是直线AD上一动点，当PO+PC取得最小值时，求点P的坐标及PO+PC的最小值；
（2）已知直线l：y＝kx+b过点（0，﹣2），且将平行四边ABCD分成面积相等的两部分，求直线l的解析式；
（3）若点N在平面直角坐标系内，在x轴上是否存在点F，使以A、C、F、N为顶点的四边形为菱形？若存在，请直接写出点F的坐标，若不存在，请说明理由．


2022-2023学年广东省汕头市龙湖实验中学九年级（上）开学
数学试卷
参考答案与试题解析
一.选择题（本题共10小题，每小题3分，共30分）
1．（3分）下列方程是关于x的一元二次方程的是（　　）
A．x+2y＝1 B．x2+x﹣1＝x2 C． D．x2﹣5x＝0
【分析】根据只含有一个未知数，并且未知数的最高次数是2的整式方程叫一元二次方程进行分析即可．
【解答】解：A．该方程是二元一次方程，故本选项不合题意；
B．该方程化简后可得x﹣1＝0，是一元一次方程，故此选项不符合题意；
C．该方程是分式方程，故本选项不合题意；
D、该方程是一元二次方程，故本选项符合题意；
故选：D．
【点评】此题主要考查了一元二次方程的定义，解题的关键是掌握判断一个方程是否是一元二次方程应注意抓住5个方面：“化简后”；“一个未知数”；“未知数的最高次数是2”；“二次项的系数不等于0”；“整式方程”．
2．（3分）以下列长度的线段为边，不能构成直角三角形的是（　　）
A．2、3、4 B．1、1、 C．3、4、5 D．5、12、13
【分析】根据勾股定理的逆定理，可以判断各个选项中的三条线段是否可以构成直角三角形，从而可以解答本题．
【解答】解：∵22+32＝4+9＝13≠16＝42，故选项A中三条线段不能构成直角三角形；
∵12+12＝1+1＝2＝（）2，故选项B中三条线段能构成直角三角形；
∵32+42＝9+16＝25＝52，故选项C中三条线段能构成直角三角形；
∵52+122＝25+144＝225＝152，故选项D中三条线段能构成直角三角形；
故选：A．
【点评】本题考查勾股定理的逆定理，解答本题的关键是明确题意，利用勾股定理的逆定理解答．
3．（3分）下列根式中属最简二次根式的是（　　）
A． B． C． D．
【分析】利用最简二次根式定义判断即可．
【解答】解：A、原式为最简二次根式，符合题意；
B、原式＝＝，不符合题意；
C、原式＝2，不符合题意；
D、原式＝，不符合题意．
故选：A．
【点评】此题考查了最简二次根式，熟练掌握最简二次根式的定义是解本题的关键．
4．（3分）下列计算正确的是（　　）
A． B． C． D．
【分析】直接利用二次根式的混合运算法则计算得出答案．
【解答】解：A、2+，无法计算，故此选项错误；
B、﹣，无法计算，故此选项错误；
C、×＝2，正确；
D、÷＝，无法计算，故此选项错误；
故选：C．
【点评】此题主要考查了二次根式的混合运算，正确化简二次根式是解题关键．
5．（3分）一组数据1，1，3，2，2，1的众数是（　　）
A．3 B．1.5 C．2 D．1
【分析】根据众数的定义即可得出答案．
【解答】解：∵1出现了3次，出现的次数最多，
∴众数是1．
故选：D．
【点评】此题考查了众数，众数是一组数据中出现次数最多的数，注意：众数不止一个．
6．（3分）菱形ABCD的两条对角线AC＝8cm，BD＝6cm，那么菱形的边长是（　　）
A．6cm B．5cm C．4cm D．8cm
【分析】由菱形对角线互相垂直平分，可得AC⊥BD，BO＝4cm，AO＝3cm，然后由勾股定理求得边长，继而求得答案．
【解答】解：四边形ABCD是菱形，
∴AC⊥BD，BO＝OD＝BD＝6＝3（cm），AO＝OC＝AC＝×8＝4（cm），
∴AB＝＝5（cm），
故选：B．
【点评】此题考查了菱形的性质以及勾股定理．此题难度不大，注意掌握数形结合思想的应用．
7．（3分）甲、乙、丙、丁四位优秀短跑选手，近期的10次百米测试平均成绩都是10.3秒，但他们成绩的方差分别是0.020、0.019、0.021、0.022（单位：秒2）．则这四人中发挥最稳定的是（　　）
A．甲 B．乙 C．丙 D．丁
【分析】根据方差的意义求解即可．
【解答】解：∵他们成绩的方差分别是0.020、0.019、0.021、0.022，
∴0.019＜0.020＜0.021＜0.022，
∴乙的方差最小，
∴这四人中发挥最稳定的是乙，
故选：B．
【点评】本题主要考查方差的意义，方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越差；反之，则它与其平均值的离散程度越小，稳定性越好．
8．（3分）对于一次函数y＝x+6，下列结论错误的是（　　）
A．函数值随自变量增大而增大
B．函数图象与x轴正方向成45°角
C．函数图象不经过第四象限
D．函数图象与x轴交点坐标是（0，6）
【分析】根据一次函数的性质对各选项进行逐一判断即可．
【解答】解：A、∵一次函数y＝x+6中k＝1＞0，∴函数值随自变量增大而增大，故A选项正确；
B、∵一次函数y＝x+6与x、y轴的交点坐标分别为（﹣6，0），（0，6），∴此函数与x轴所成角度的正切值＝＝1，∴函数图象与x轴正方向成45°角，故B选项正确；
C、∵一次函数y＝x+6中k＝1＞0，b＝6＞0，∴函数图象经过一、二、三象限，故C选项正确；
D、∵令y＝0，则x＝﹣6，∴一次函数y＝x+6与x轴的交点坐标分别为（﹣6，0），故D选项错误．
故选：D．
【点评】本题考查的是一次函数的性质，熟知一次函数的增减性及与坐标轴的交点坐标是解答此题的关键．
9．（3分）三角形的三边长为a，b，c，且满足（a+b）2＝c2+2ab，则这个三角形是（　　）
A．等边三角形 B．钝角三角形 C．直角三角形 D．锐角三角形
【分析】对等式进行整理，再判断其形状．
【解答】解：化简（a+b）2＝c2+2ab，得，a2+b2＝c2所以三角形是直角三角形，
故选：C．
【点评】本题考查了直角三角形的判定：可用勾股定理的逆定理判定．
10．（3分）如图，已知直线l：y＝x，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2；…；按此作法继续下去，则点B2020的坐标为（　　）

A．（2020，2020） B．（4040，4040）
C．（42020•，42020） D．（22020•，22020）
【分析】根据所给直线解析式可得l与x轴的夹角，进而根据所给条件依次得到点B1，B2的坐标，通过相应规律得到B2020坐标即可．
【解答】解：∵直线l：y＝x，
∴l与x轴的夹角为30°，
∵AB∥x轴，
∴∠ABO＝30°，
∵OA＝1，
∴AB＝，
∴B（，1），
∵A1B⊥l，
∴∠ABA1＝60°，
∴AA1＝3，
∴A1（0，4），
把y＝4代入y＝x，求得x＝4，
∴B1（4，4）
同理可得B2（16，16），
…，
∴B2020（42020•，42020）．
故选：C．
【点评】此题考查的是一次函数综合题，先根据所给一次函数判断出一次函数与x轴夹角是解决本题的突破点；根据含30°的直角三角形的特点依次得到B、B1、B2、B3…的点的坐标是解决本题的关键．
二.填空题（本大题共7小题，每小题4分，共28分）
11．（4分）计算：＝　5　．
【分析】根据二次根式的基本性质进行解答即可．
【解答】解：原式＝＝5．
故答案为：5．
【点评】本题考查的是二次根式的性质与化简，熟知二次根式的基本性质是解答此题的关键．
12．（4分）已知三角形三边长分别是6，8，10，则此三角形的面积为 　24　．
【分析】根据三角形三边长，利用勾股定理逆定理求证此三角形是直角三角形，然后即可求得面积．
【解答】解：∵62+82＝102，
∴此三角形为直角三角形，
∴此三角形的面积为：×6×8＝24．
故答案为：24．
【点评】此题主要考查学生对勾股定理逆定理的理解和掌握，解答此题的关键是利用勾股定理逆定理求证此三角形是直角三角形．
13．（4分）如图，△ABC中，三条中位线围成的△DEF的周长是15cm，则△ABC的周长是 　30　cm．

【分析】根据三角形的周长公式、三角形中位线定理解答即可．
【解答】解：∵△DEF的周长是15，
∴DE+DF+EF＝15，
∵DE、DF、EF分别是△ABC的中位线，
∴BC＝2DE，AC＝2DF，AB＝2EF，
∴△ABC的周长＝BC+AC+AB＝2（DE+DF+EF）＝30（cm），
故答案为：30．
【点评】本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
14．（4分）若y＝（m+1）x|m|+3是关于x的一次函数，则m＝　1　．
【分析】根据一次函数定义可得：|m|＝1，且m+1≠0，再解即可．
【解答】解：由题意得：|m|＝1且m+1≠0，
解得：m＝1，
故答案为：1．
【点评】此题主要考查了一次函数定义，关键是掌握一次函数解析式y＝kx+b的结构特征：k≠0；自变量的次数为1；常数项b可以为任意实数．
15．（4分）一次函数y＝kx+b与y＝2x+1平行，且经过点（﹣3，4），则表达式为：　y＝2x+10　．
【分析】根据一次函数与y＝2x+1平行，可求得k的值，再把点（﹣3，4）代入即可求得一次函数的解析式．
【解答】解：∵一次函数y＝kx+b与y＝2x+1平行，
∴k＝2，
又∵函数经过点（﹣3，4）
∴4＝﹣6+b，解得：b＝10
∴函数的表达式为y＝2x+10．
【点评】本题考查了待定系数法求一次函数的解析式，比较简单，同学们要熟练掌握．
16．（4分）若x＝3是关于x的一元二次方程x2﹣mx﹣3＝0的一个解，则m的值是　2　．
【分析】根据x＝3是已知方程的解，将x＝3代入方程即可求出m的值．
【解答】解：将x＝3代入方程得：9﹣3m﹣3＝0，
解得：m＝2．
故答案为：2．
【点评】本题考查了一元二次方程的解．解题的关键是掌握一元二次方程的解的定义：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．
17．（4分）如图，在矩形ABCD中，AB＝6，AD＝8，以A为圆心，任意长为半径画弧交AB，AC于M，N，再分别以M，N为圆心，大于MN为半径画弧，两弧交于点G，连接AG，交边BC于E，则△AEC的周长为　15+3　．

【分析】作EF⊥AC于F，由题意得AE平分∠BAC，证Rt△AEF≌Rt△AEB（HL），得出AF＝AB＝6，CF＝AC﹣AF＝4，设EF＝EB＝x，则CE＝8﹣x，在Rt△CEF中，由勾股定理得出方程，解方程得出EF＝3，由三角形周长公式即可得出答案．
【解答】解：作EF⊥AC于F，如图：
由题意得：AE平分∠BAC，
∵四边形ABCD是矩形，
∴∠B＝90°，BC＝AD＝8，
∴AC＝＝＝10，
EB⊥AB，
∵AE平分∠BAC，
∴EF＝EB，
在Rt△AEF和Rt△AEB中，，
∴Rt△AEF≌Rt△AEB（HL），
∴AF＝AB＝6，
∴CF＝AC﹣AF＝4，
设EF＝EB＝x，则CE＝8﹣x，
在Rt△CEF中，由勾股定理得：x2+42＝（8﹣x）2，
解得：x＝3，
∴BE＝3，
∴CE＝5，
∴AE＝＝3，
∴△AEC的周长为15+3，
故答案为：15+3．

【点评】本题考查了作图﹣基本作图，矩形的性质、角平分线的性质、全等三角形的判定与性质以及勾股定理等知识；熟练掌握全等三角形的判定与性质，由勾股定理得出方程是解题的关键．
三、解答题（一）（本大题共3小题，每小题6分，共18分）
18．（6分）计算：．
【分析】直接利用零指数幂的性质以及二次根式的性质、绝对值的性质、负整数指数幂的性质分别化简，进而计算得出答案．
【解答】解：原式＝2﹣（﹣1）﹣1+2
＝2﹣+1﹣1+2
＝+2．
【点评】此题主要考查了实数的运算，正确化简各数是解题关键．
19．（6分）先化简后求值：，其中．
【分析】先对分式分母进行分式因解，把除法部分化成乘法形式，再进行化简求值．
【解答】解：
＝
＝
＝
＝﹣，
当x＝﹣1时，﹣＝﹣＝﹣．
【点评】本题考查了学生对分式综合运算能力，式子比较复杂，做题过程中要细心，综合性比较强．
20．（6分）如图，在▱ABCD中，DE⊥AC于E，BF⊥AC于F，∠DAE＝35°．
（1）求证：△AED≌△CFB；
（2）求∠CBF的度数．

【分析】（1）利用平行四边形的性质得出AD＝BC，∠DAE＝∠BCA，进而利用全等三角形的判定得出即可；
（2）在Rt△ADE中根据∠DAE＝35°，∠DEA＝C＝90°得到∠ADE＝90°﹣∠DAE＝55°，然后根据△AED≌△CFB，求得∠CBF＝∠ADE＝55°．
【解答】（1）证明：在平行四边形ABCD中，AD＝CB，
又AD∥BC，
∴∠DAE＝∠BCF，
∵DE⊥AC，BF⊥AC．
∴∠DEA＝∠BFC＝90°，
在△AED和△CFB中，
，
∴△AED≌△CFB（AAS）；
（2）解：在Rt△ADE中，∠DAE＝35°，∠DEA＝C＝90°，
∠ADE＝90°﹣∠DAE＝55°，
∵△AED≌△CFB（AAS），
∴∠CBF＝∠ADE＝55°．
【点评】考查了平行四边形的性质及全等三角形的判定与性质，得出△ADE≌△CBF是解题关键．
四、解答题（二）（本大题3小题，每小题8分，共24分）
21．（8分）如图，已知一次函数y＝kx+b的图象经过A（﹣2，﹣1），B（1，3）两点，并且交x轴于点C，交y轴于点D．
（1）求该一次函数的解析式；
（2）求△AOB的面积．

【分析】（1）先把A点和B点坐标代入y＝kx+b得到关于k、b的方程组，解方程组得到k、b的值，从而得到一次函数的解析式；
（2）先确定D点坐标，然后根据三角形面积公式和△AOB的面积＝S△AOD+S△BOD进行计算．
【解答】解：（1）把A（﹣2，﹣1），B（1，3）代入y＝kx+b得，
解得．
所以一次函数解析式为y＝x+；
（2）把x＝0代入y＝x+得y＝，
所以D点坐标为（0，），
所以△AOB的面积＝S△AOD+S△BOD
＝××2+××1
＝．
【点评】本题考查了待定系数法求一次函数解析式：（1）先设出函数的一般形式，如求一次函数的解析式时，先设y＝kx+b；（2）将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；（3）解方程或方程组，求出待定系数的值，进而写出函数解析式．
22．（8分）在一次大学生一年级新生训练射击训练中，某小组的成绩如表：
环数
6
7
8
9
人数
1
5
3
1
（1）该小组射击数据的众数是 　7　，中位数是 　7　；
（2）求该小组的平均成绩；
（3）若8环（含8环）以上为优秀射手，在1200名新生中有多少人可以评为优秀射手？
【分析】（1）根据众数和中位数的定义即可得出答案；
（2）根据平均数的计算公式进行计算即可；
（3）用1200乘以优秀选手所占的百分比即可得出答案．
【解答】解：（1）∵射击7环数的人数有5个，人数最多，
∴该小组射击数据的众数是7；
共10人，中位数为第5和第6人的平均数，即＝7，
故答案为：7，7；

（2）该小组的平均成绩为：（6+7×5+8×3+9）＝7.4（环）；

（3）根据题意得：
1200×＝480（名），
答：在1200名新生中有480名可以评为优秀射手．
【点评】此题考查了众数、平均数和用样本估计总体，掌握众数的定义、用样本估计总体和平均数的计算公式是本题的关键．
23．（8分）某商场计划购进A，B两种新型节能台灯共100盏，这两种台灯的进价、售价如表所示：
类型价格
进价（元/盏）
售价（元/盏）
A型
30
45
B型
50
70
（1）若商场预计进货款为3500元，则这两种台灯各购进多少盏？
（2）若商场规定B型台灯的进货数量不超过A型台灯数量的3倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？
【分析】（1）设商场应购进A型台灯x盏，表示出B型台灯为（100﹣x）盏，然后根据进货款＝A型台灯的进货款+B型台灯的进货款列出方程求解即可；
（2）设商场销售完这批台灯可获利y元，根据获利等于两种台灯的获利总和列式整理，再求出x的取值范围，然后根据一次函数的增减性求出获利的最大值．
【解答】解：（1）设商场应购进A型台灯x盏，则B型台灯为（100﹣x）盏，
根据题意得，30x+50（100﹣x）＝3500，
解得x＝75，
所以，100﹣75＝25，
答：应购进A型台灯75盏，B型台灯25盏；

（2）设商场销售完这批台灯可获利y元，
则y＝（45﹣30）x+（70﹣50）（100﹣x），
＝15x+2000﹣20x，
＝﹣5x+2000，
即y＝﹣5x+2000，
∵B型台灯的进货数量不超过A型台灯数量的3倍，
∴100﹣x≤3x，
∴25≤x≤100，
∵k＝﹣5＜0，y随x的增大而减小，
∴x＝25时，y取得最大值，为﹣5×25+2000＝1875（元）
答：商场购进A型台灯25盏，B型台灯75盏，销售完这批台灯时获利最多，此时利润为1875元．
【点评】本题考查了一次函数的应用，主要利用了一次函数的增减性，（2）题中理清题目数量关系并列式求出x的取值范围是解题的关键．
五、解答题（三）（本大题2小题，每小题10分，共20分）
24．（10分）如图，直线AB为y＝kx+6，D（8，0），点O关于直线AB的对称点C在直线AD上．
（1）求直线AD的解析式．
（2）求点C的坐标．
（3）若OC交AB于点E，在线段AD上是否存在一点F，使△ABC与△AEF的面积相等？若存在求出F点坐标，若不存在，请说明理由．

【分析】（1）求出A（0，6），然后用待定系数法即可求直线解析式；
（2）利用折叠的性质以及勾股定理求出点B的坐标，设C（x，﹣x+6），由∠OAB＝∠COB，利用三角形函数值求出x，即可得点C的坐标；
（3）由面积相等可推导出BF∥OC，求出直线BF的解析式为y＝x﹣，联立方程即可求F点坐标．
【解答】解：（1）∵y＝kx+6，
∴A（0，6），
∵D（8，0），
设直线AD的解析式为y＝k′x+6，
∴8k′+6＝0，解得k′＝﹣，，
∴直线AD的解析式为y＝﹣x+6；

（2）在Rt△AOD中，AD＝＝10，
∵点O、点C关于直线AB对称，
∴设OB＝BC＝a，OA＝AC＝6，
∴CD＝AD﹣AC＝4，BD＝8﹣a，
在Rt△BCD中，a2+42＝（8﹣a）2，
∴a＝3，
∴B（3，0），
∵C点在直线AD上，
∴设C（x，﹣x+6），
∵OE⊥AB，OA⊥OB，
∴∠OAB＝∠COB，
∴tan∠OAB＝tan∠COB，
∴，
∴x＝，
∴C（，）；

（3）如图：连接BF，

∵△ABC与△AEF的面积相等，
∴△BEC与△ECF的面积相等，
∴BF∥OC，
∵C（，），
直线OC的解析式为y＝x，
设直线BF的解析式为y＝x+n，
∵B（3，0）在直线BF上，
∴b＝﹣，
∴直线BF的解析式为y＝x﹣，
联立x﹣＝﹣x+6，
∴x＝6，
∴F（6，）．
【点评】本题是一次函数综合题，考查了待定系数法，轴对称的性质，勾股定理，锐角三角函数等知识，利用数形结合思想解决问题是解题的关键．
25．（10分）阅读理解：在平面直角坐标系中，任意两点A（x1，y1），B（x2，y2），则①AB两点的距离＝；②线段AB的中点坐标为（，）．
解决问题：
如图，平行四边形ABCD中，点B在x轴负半轴上，点D在第一象限，A，C两点的坐标分别为（0，4），（3，0），边AD的长为6．
（1）若点P是直线AD上一动点，当PO+PC取得最小值时，求点P的坐标及PO+PC的最小值；
（2）已知直线l：y＝kx+b过点（0，﹣2），且将平行四边ABCD分成面积相等的两部分，求直线l的解析式；
（3）若点N在平面直角坐标系内，在x轴上是否存在点F，使以A、C、F、N为顶点的四边形为菱形？若存在，请直接写出点F的坐标，若不存在，请说明理由．

【分析】（1）“将军饮马”模型：设点O关于直线AD的对称点为Q，连接CQ交AD于P，连接OP，求出直线QC的解析式为，即得P（，4），PO+PC的最小值＝QC＝；
（2）设AC与BD交于点E，则直线l经过点E，由A（0，4）C（3，0），得点E的坐标为，用待定系数法即可求得直线l的解析式为y＝x﹣2；
（3）分类画出图象：①以AC为边时，可得CF1＝CF2＝AC＝5，即得F1（8，0），F2（﹣2，0），当F3与B重合时，四边形AF3N3C为菱形，可得F3（﹣3，0）；
②以AC为对角线时，设此时F4（t，0），由AF4＝CF4可得：＝|3﹣t|，即可求出F4（﹣，0）．
【解答】解：（1）设点O关于直线AD的对称点为Q，连接CQ交AD于P，连接OP，如图：

∵A（0，4），
∴Q（0，8），PO＝PQ，
∵C（3，0），
∴设直线QC的解析式为y＝kx+b（k≠0），则，解得：，
∴直线QC的解析式为，
当y＝4时，4＝﹣x+8，
解得x＝，
∴P（，4），
∴PO+PC的最小值＝；
（2）设AC与BD交于点E，由平行四边形的中心对称性可知，直线l将平行四边ABCD分成面积相等的两部分，则直线l经过点E，
如图：

在平行四边形ABCD中，EA＝EC，
∵A（0，4）C（3，0），
∴点E的坐标为，
设直线l的解析式为y＝mx+n（m≠0），则，
解得：，
∴直线l的解析式为y＝x﹣2；
（3）存在，理由如下：
①∵A（0，4），C（3，0），
∴AC＝5，
以AC为边时，如图：

此时CF1＝CF2＝AC＝5，
∴F1（8，0），F2（﹣2，0），
当F3与B重合时，如图：

此时AC＝AF3，过B（F3）作AC平行线，过C作AB（AF3）的平行线，两平行线交于N3，此时四边形AF3N3C为菱形，
∴F3（﹣3，0），
②以AC为对角线时，如图：

设此时F4（t，0），由AF4＝CF4可得：＝|3﹣t|，
解得t＝﹣，
∴F4（﹣，0），
综上所述，以A、C、F、N为顶点的四边形为菱形，点F的坐标为（8，0）或（﹣2，0）或（﹣3，0）或（，0）．
【点评】本题考查平行四边形性质及应用，涉及待定系数法，一次函数图象、“将军饮马”问题等知识，解题的关键是分类画出图形，数形结合解决问题．