初中数学人教版九年级上册第二十三章 旋转23.1 图形的旋转导学案及答案

《旋转》第一节 图形的旋转导学案1

主编人：  主审人：

班级：          学号：        姓名：    

学习目标：

【知识与技能】

通过具体实例认识图形的旋转，理解“对应点到旋转中心的距离相等”以及“旋转前、后的图形全等”的基本性质。

【过程与方法】

经历对具有旋转特征的图形进行观察、分析、动手操作和画图等过程，按要求作出简单平面图形旋转后的图形。

【情感、态度与价值观】

学生在经历了实际探究、知识应用及内化等数学活动中，体验数学的具体、生动、灵活，调动学生学习的数学的主动性。

培养学生初步的审美能力，增强对图形的欣赏意识.。

【重点】

对生活中的旋转现象作数学上的分析，理解旋转的定义。

【难点】

对旋转现象进行分析研究，旋转后的现象进行探索。

学习过程:

一、自主学习

（一）复习巩固

1. 把一个平面图形绕着平面内某一点O转动一个角度的图形变换叫做      ．点O叫做     ，转动的角叫做       ．

2. 一般地，可以根据定义得出旋转的以下性质：

（1）对应点到旋转中心的距离      ．

（2）对应点与旋转中心所连线段的夹角等于     ．

（3）旋转前、后的图形       ．

（二）自主探究

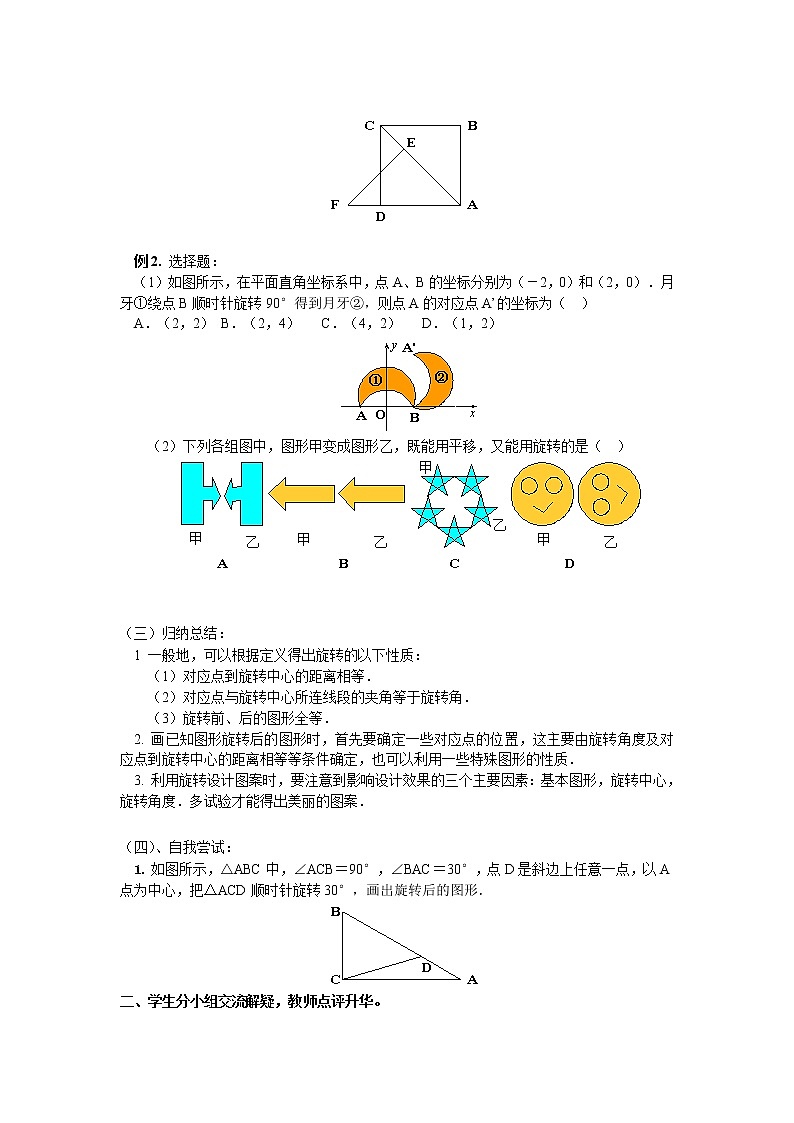
例1. 如图所示，AC是正方形ABCD的对角线，△ABC经过旋转后到达△AEF的位置，则旋转中心是哪点？旋转方向是什么？旋转角度是多少？点B的对应点是什么？

例2. 选择题：

（1）如图所示，在平面直角坐标系中，点A、B的坐标分别为（－2，0）和（2，0）．月牙①绕点B顺时针旋转90°得到月牙②，则点A的对应点A’的坐标为（   ）

A．（2，2）  B．（2，4）      C．（4，2）      D．（1，2）

（2）下列各组图中，图形甲变成图形乙，既能用平移，又能用旋转的是（   ）

（三）归纳总结：

1 一般地，可以根据定义得出旋转的以下性质：

（1）对应点到旋转中心的距离相等．

（2）对应点与旋转中心所连线段的夹角等于旋转角．

（3）旋转前、后的图形全等．

2. 画已知图形旋转后的图形时，首先要确定一些对应点的位置，这主要由旋转角度及对应点到旋转中心的距离相等等条件确定，也可以利用一些特殊图形的性质．

3. 利用旋转设计图案时，要注意到影响设计效果的三个主要因素：基本图形，旋转中心，旋转角度．多试验才能得出美丽的图案．

（四）、自我尝试：

1. 如图所示，△ABC中，∠ACB＝90°，∠BAC＝30°，点D是斜边上任意一点，以A点为中心，把△ACD顺时针旋转30°，画出旋转后的图形．

二、学生分小组交流解疑，教师点评升华。

三、课堂检测：

一. 选择题

1. 下面生活中的实例，不是旋转的是（   ）

A. 传送带传送货物                          B. 螺旋桨的运动

C. 风车风轮的运动                           D. 自行车车轮的运动

2. 中国国旗上有五个五角星，其中四个小五角星可以看作是其中一个旋转得到的，旋转中心是（   ）

A. 最上面的小五角星中心                B. 最下面的小五角星中心

C. 大五角星中心                              D. 长方形左上角的顶点

3. 将一个三角形旋转，旋转中心应选在（   ）

A. 三角形的顶点                              B. 三角形的外部

C. 三角形的三条边上                       D. 平面内的任意位置

4. 如图，将△ABC绕点A逆时针旋转80°得到△AB′C′.若∠BAC=50°，则∠CAB′的度数为（   ）

A. 30°                  B. 40°                C. 50°                   D. 80°

5. 将叶片图案旋转180°后，得到的图形是（   ）

**6. 数学课上，老师让同学们观察如图所示的图形，问：它绕着圆心O旋转多少度后和它自身重合？甲同学说：45°；乙同学说：60°；丙同学说：90°；丁同学说：135°．以上四位同学的回答中，错误的是（   ）

A. 甲                    B. 乙                   C. 丙                      D. 丁

7. 如果4张扑克按图1的形式摆放在桌面上，将其中一张旋转180°后，扑克的放置情况如图2所示，那么旋转的扑克从左起是（   ）

A. 第一张             B. 第二张            C. 第三张               D. 第四张

*8. 如图所示，请你先观察（1）～（3），然后确定第四张为（   ）

A.                 B.                C.                   D.

二. 填空题

1. 图形的旋转是由__________和__________所决定的，旋转不改变图形的__________．

2. 由8时15分到8时40分，时钟的分针旋转的角度为__________，时针旋转的角度为__________．

3. 如图所示，其中的图（2）可以看作是由图（1）经过__________次旋转，每次旋转__________得到的．

三. 解答题

1. 如图所示，已知△ABC和旋转中心点O及点A的对应点D，请画出△ABC旋转后的图形△DEF．

2. 如图所示，某战士在训练场上练习射击，发现子弹均击中靶子上的阴影部分，你知道阴影部分的面积是多少吗？