















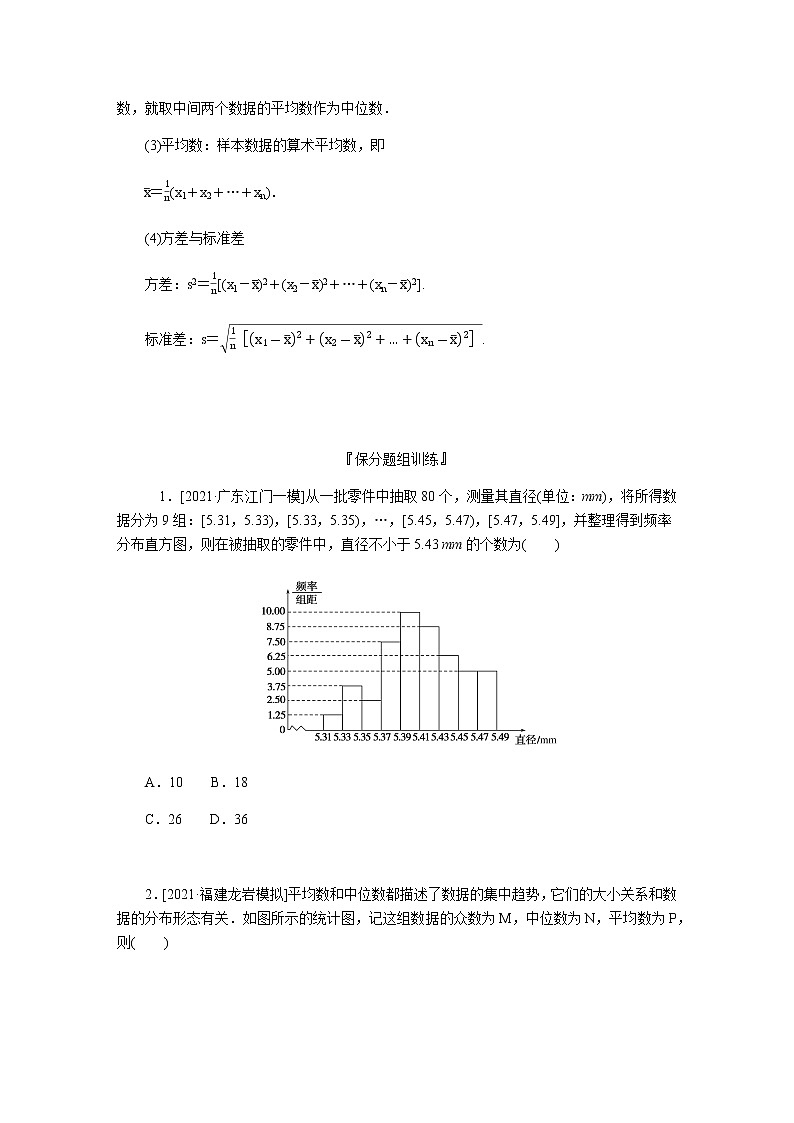
所属成套资源:全套新高考高中数学二轮复习专题导学案+PPT课件+课时作业+详解答案
新高考高中数学二轮复习专题五概率与统计导学案+PPT课件
展开这是一份新高考高中数学二轮复习专题五概率与统计导学案+PPT课件,文件包含152pptx、151pptx、152DOCX、151DOCX等4份课件配套教学资源,其中PPT共85页, 欢迎下载使用。
第1讲 概率、统计、统计案例、正态分布——小题备考
微专题1用样本估计总体
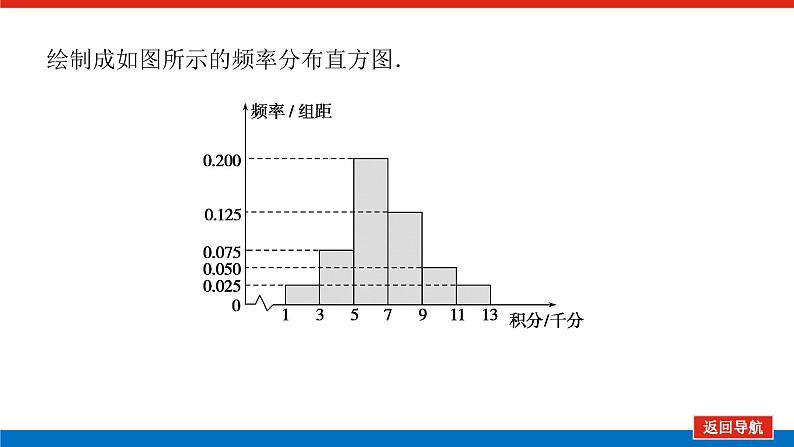
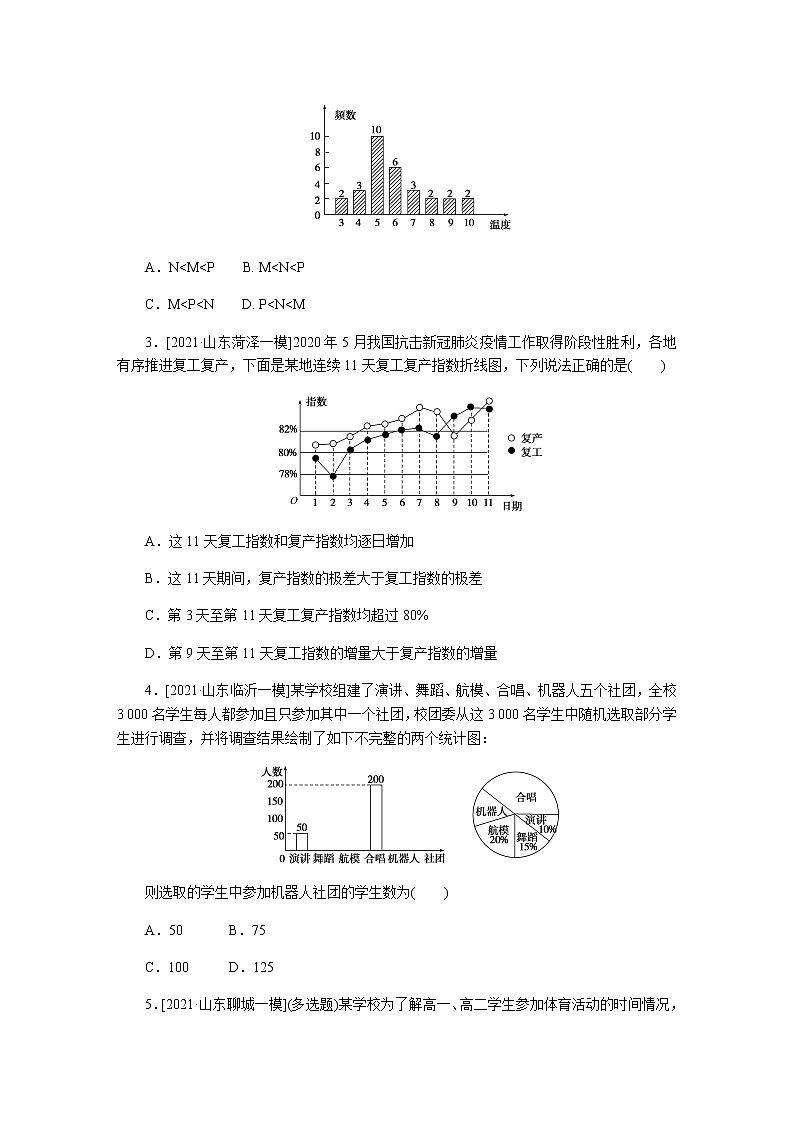
『保分题组训练』 1.[2021·广东江门一模]从一批零件中抽取80个,测量其直径(单位:mm),将所得数据分为9组:[5.31,5.33),[5.33,5.35),…,[5.45,5.47),[5.47,5.49],并整理得到频率分布直方图,则在被抽取的零件中,直径不小于5.43 mm的个数为( )A.10 B.18 C.26 D.36
解析:由频率分布直方图可知,直径不小于5.43 mm的频率为(6.25+5+5)×0.02=0.325,故在被抽取的零件中,直径不小于5.43 mm的个数为0.325×80=26个.故选C.
C
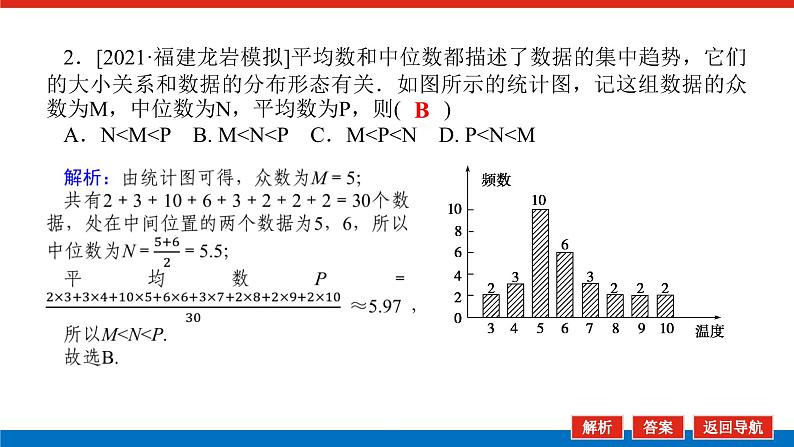
2.[2021·福建龙岩模拟]平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据的分布形态有关.如图所示的统计图,记这组数据的众数为M,中位数为N,平均数为P,则( )A.N
B
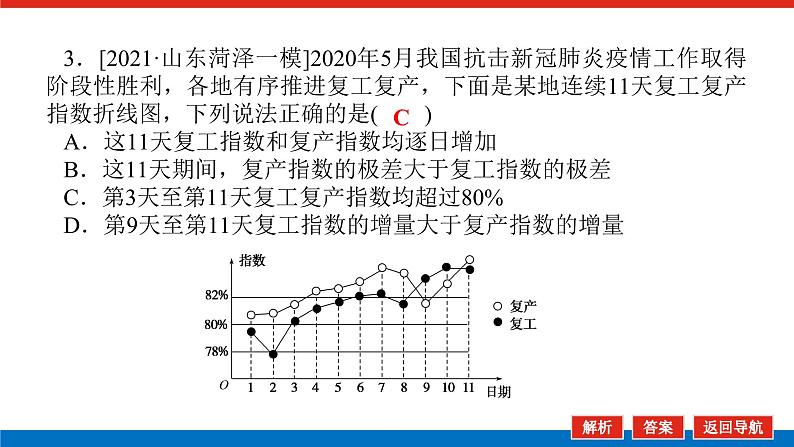
3.[2021·山东菏泽一模]2020年5月我国抗击新冠肺炎疫情工作取得阶段性胜利,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是( )A.这11天复工指数和复产指数均逐日增加B.这11天期间,复产指数的极差大于复工指数的极差C.第3天至第11天复工复产指数均超过80%D.第9天至第11天复工指数的增量大于复产指数的增量
C
解析:第8天比第7天的复工指数和复产指数均低,A错误;这11天期间,复产指数的极差小于复工指数的极差:两者最高差不多,但最低的复工指数比复产指数低得多,B错误;第3天至第11天复工复产指数均超过80%,C正确;第9天至第11天复工指数的增量小于复产指数的增量,D错误.故选C.
4.[2021·山东临沂一模]某学校组建了演讲、舞蹈、航模、合唱、机器人五个社团,全校3 000名学生每人都参加且只参加其中一个社团,校团委从这3 000名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:则选取的学生中参加机器人社团的学生数为( )A.50 B.75C.100 D.125
B
5.[2021·山东聊城一模](多选题)某学校为了解高一、高二学生参加体育活动的时间情况,分别统计了这两个年级学生某周的活动时间,并制成了如图所示的条形图进行比较.则下列说法中正确的是( )A.高二年级学生周活动时间的众数比高一年级的大B.高二年级学生周活动时间的平均值比高一年级的小C.高二年级学生周活动时间的中位数比高一年级的大D.高二年级学生周活动时间的方差比高一年级的小
ACD
【技法领悟】众数、中位数、平均数与直方图的关系1.众数为频率分布直方图中最高矩形的底边中点的横坐标.2.中位数为平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标.3.平均数等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之积的和.
微专题2变量间的相关关系、统计案例
B
CD
1.75
0.025
5
微专题3概率问题
显然,对任意的x∈R,f(x)>0,它的图象在x轴的上方.可以证明x轴和曲线之间的区域的面积为1.我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线,如图所示.若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布(normal distribution),记为X~N(μ,σ2).特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布.
若X~N(μ,σ2),则如图所示,X取值不超过x的概率P(X≤x)为图中区域A的面积,而P(a≤X≤b)为区域B的面积.(2)正态总体三个基本概念值①P(μ-σ≤X≤μ+σ)≈0.682 7;②P(μ-2σ≤X≤μ+2σ)≈0.954 5;③P(μ-3σ≤X≤μ+3σ)≈0.997 3.
B
A
解析:∵随机变量X服从正态分布N(10,σ2),P(X<8)=0.23,∴P(X>12)=0.23,∴P(X<12)=1-0.23=0.77.
0.77
A
ABC
ACD
【技法领悟】1.求复杂事件概率的两种方法:(1)直接法:正确分析复杂事件的构成,将复杂事件转化为几个彼此互斥的事件的和事件或几个相互独立事件同时发生的积事件或一独立重复试验问题,然后用相应概率公式求解.(2)间接法:当复杂事件正面情况比较多,反面情况较少,则可利用其对立事件进行求解.对于“至少”“至多”等问题往往也用这种方法求解.2.利用正态曲线的对称性求概率的策略:(1)解题的关键是利用对称轴x=μ确定所求概率对应的随机变量的区间与已知概率对应的随机变量的区间的关系,必要时,可借助图形判断.
(2)对于正态分布N(μ,σ2),由x=μ是正态曲线的对称轴知:①对任意的a,有P(X<μ-a)=P(X>μ+a);②P(X
相关课件
这是一份新高考数学二轮复习专题五规范答题5概率与统计课件,共7页。PPT课件主要包含了思路分析等内容,欢迎下载使用。
这是一份新高考数学二轮复习专题五培优点7概率与统计的创新问题课件,共47页。PPT课件主要包含了内容索引,概率和数列的综合,考点一,规律方法,所以X的分布列为,概率和函数的综合,考点二,令p1p2=t,易错提醒,分布列为等内容,欢迎下载使用。
这是一份2023届高考数学二轮复习专题五概率与统计培优提能概率与统计的创新问题课件,共24页。












