初中数学北师大版九年级下册7 切线长定理教学ppt课件

这是一份初中数学北师大版九年级下册7 切线长定理教学ppt课件，共16页。PPT课件主要包含了切线长等内容，欢迎下载使用。

(1)过圆外一点画圆的切线，这点和切点之间的线段长叫做这点到圆的_________． (2)切线长定理：过圆外一点所画的圆的两条切线长_______． 练习：如图PA，PB是⊙O的切线，切点是A，B，若PB＝5 cm，则PA的长为______ cm.
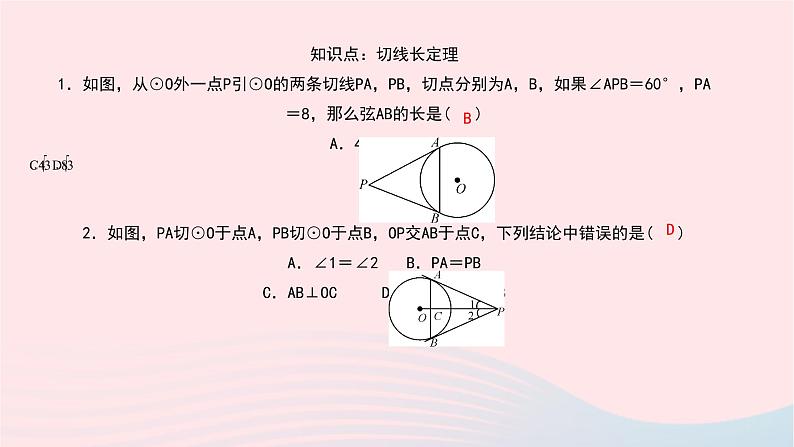
知识点：切线长定理 1．如图，从⊙O外一点P引⊙O的两条切线PA，PB，切点分别为A，B，如果∠APB＝60°，PA＝8，那么弦AB的长是( ) A．4 B．8 2．如图，PA切⊙O于点A，PB切⊙O于点B，OP交AB于点C，下列结论中错误的是( ) A．∠1＝∠2 B．PA＝PB C．AB⊥OC D．∠PAB＝∠APB
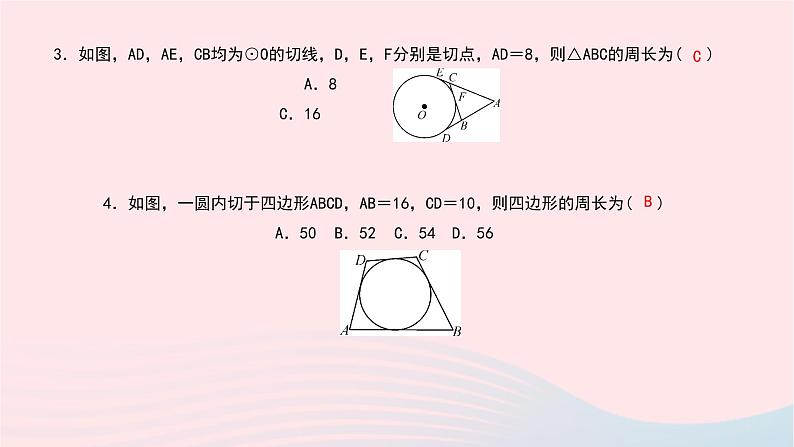
3．如图，AD，AE，CB均为⊙O的切线，D，E，F分别是切点，AD＝8，则△ABC的周长为( ) A．8 B．12 C．16 D．不能确定 4．如图，一圆内切于四边形ABCD，AB＝16，CD＝10，则四边形的周长为( ) A．50B．52 C．54 D．56
5．如图，△MBC中，∠B＝90°，∠C＝60°，MB＝2 ，点A在MB上，以AB为直径作⊙O与MC相切于点D，则CD的长为____． 6．如图，AC⊥BC于点C，BC＝a，CA＝b，AB＝c，⊙O与直线AB，BC，AC都相切，则⊙O的半径等于_______.
7．如图，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径，AC，PB的延长线相交于点D. (1)若∠1＝20°，求∠APB的度数； (2)当∠1为多少度时，OP＝OD，并说明理由．
解：(1)∵PA，PB为切线，∴∠PAO＝90°.∵∠1＝20°，∴∠PAB＝70°.∵PA＝PB，∴∠PAB＝∠PBA＝70°，∴∠APB＝40°. (2)当∠1＝30°时，OP＝OD，理由：∵∠1＝30°，∴∠PAB＝60°，∴△PAB是等边三角形，∴∠ABP＝60°＝∠1＋∠D，∴∠D＝30°，∴∠1＝∠D，∴AB＝BD，∴BP＝BD且OB⊥PD，∴OB垂直平分PD，∴OP＝OD.
8．如图，在Rt△ABC中，∠C＝90°，BC＝5，⊙O是△ABC的内切圆，切点分别为D，E，F，⊙O的半径为2.求△ABC的周长．
解：连接OE，OF，∴OE⊥BC，OF⊥AC， 又∠C＝90°，∴四边形OECF为矩形． 又∵OE＝OF，∴四边形OECF为正方形．∴EC＝CF＝OE＝2， ∴BE＝BD＝5－2＝3.设AD＝AF＝x， 在Rt△ABC中 ，52＋(2＋x)2＝(3＋x)2，∴x＝10， ∴△ABC的周长＝AB＋BC＋AF＝13＋5＋12＝30.
9．如图，在等腰直角三角形ABC中，AB＝AC＝4，点O为BC的中点，以点O为圆心作⊙O交BC于点M，N，⊙O与AB，AC相切，切点分别为D，E，则⊙O的半径和∠MND的度数分别为( ) A．2，22.5° B．3，30° C．3，22.5° D．2，30°
10．如图，在Rt△ABC中，∠ACB＝90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E. (1)求证：EB＝EC； (2)若以点O，D，E，C为顶点的四边形是正方形， 试判断△ABC的形状，并说明理由．
11．如图，PA，PB分别切⊙O于A，B，连接PO与AB相交于D，C是⊙O上一点，∠C＝60°. (1)求∠APB的大小； (2)若PO＝20 cm，求△AOB的面积．
12．如图，AB是⊙O的直径，AM和BN是它的两条切线，DE切⊙O于点E，交AM于点D，交BN于点C，点F是CD的中点，连接OF. (1)求证：OD∥BE； (2)猜想：OF与CD有何数量关系？并说明理由．