2020-2021学年浙江省绍兴市柯桥区联盟校八年级（下）月考数学试卷（3月份）(含答案)

这是一份2020-2021学年浙江省绍兴市柯桥区联盟校八年级（下）月考数学试卷（3月份）(含答案)，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2020-2021学年浙江省绍兴市柯桥区联盟校八年级（下）月考数学试卷（3月份）
一、选择题（本大题有10小题，每小题2分，共20分）
1．（2分）下列方程中为一元二次方程的是（　　）
A．x2＝1 B．（x+2）（x﹣1）＝x2
C．10y＝4x2 D．x2+＝3
2．（2分）数据10，10，10，11，12，12，13，13的众数是（　　）
A．10 B．11 C．12 D．13
3．（2分）下列各式中能与合并的二次根式的是（　　）
A． B． C． D．
4．（2分）关于x的一元二次方程（a﹣1）x2+x+a2﹣1＝0的一个根是0，则a的值为（　　）
A．1 B．﹣1 C．1或﹣1 D．0
5．（2分）小林在计算时遇到以下情况，结果正确的是（　　）
A．＝5+12＝17
B．﹣2
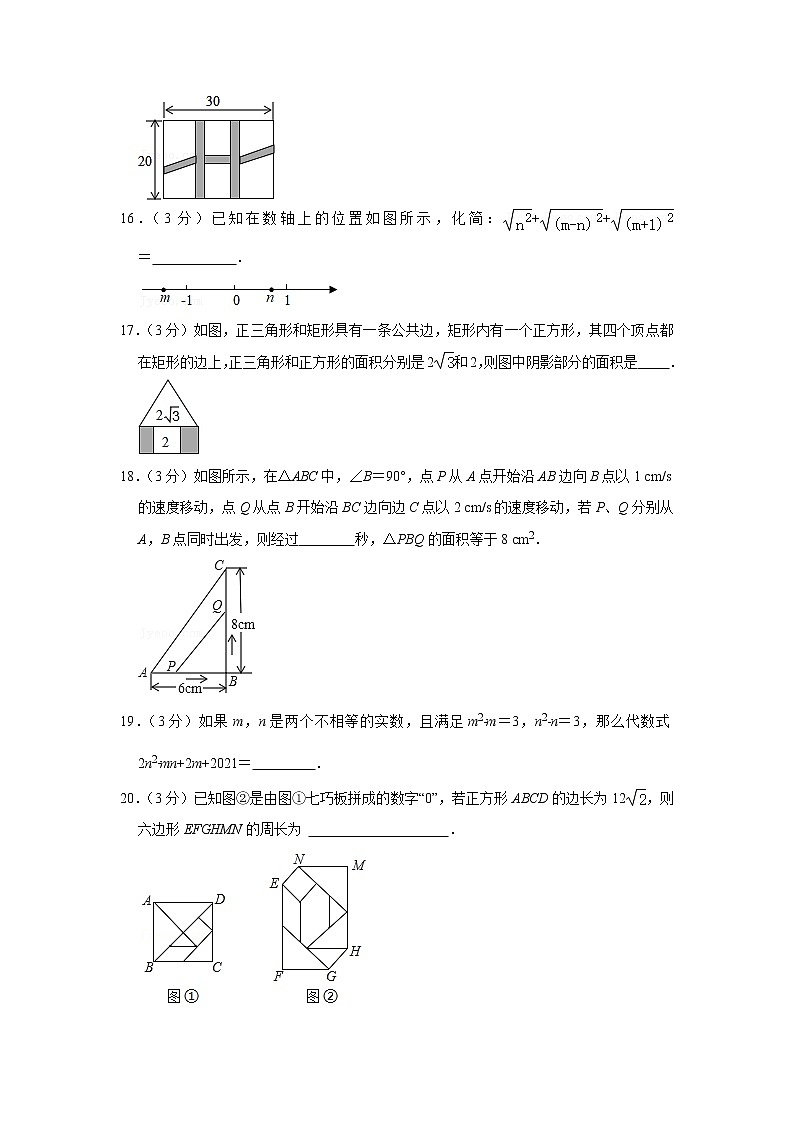
C．
D．
6．（2分）在四边形ABCD中，∠A+∠C＝180°，∠B比∠D大60°，则∠B的度数为（　　）
A．60° B．80° C．120° D．130°
7．（2分）已知方程x2﹣6x+q＝0可以配方成（x﹣p）2＝7的形式，那么x2﹣6x+q＝2可以配方成下列的（　　）
A．（x﹣p）2＝5 B．（x﹣p）2＝9 C．（x﹣p+2）2＝9 D．（x﹣p+2）2＝5
8．（2分）根据下列表格的对应值：
x
0.59
0.60
0.61
0.62
0.63
x2+x﹣1
﹣0.061
﹣0.04
﹣0.017
0.004 4
0.026 9
判断方程x2+x﹣1＝0一个解的取值范围是（　　）
A．0.59＜x＜0.61 B．0.60＜x＜0.61
C．0.61＜x＜0.62 D．0.62＜x＜0.63
9．（2分）若t是方程ax2+2x+c＝0（a≠0）的一个根，设P＝1﹣ac，Q＝（at+1）2，则P与Q的大小关系正确的是（　　）
A．P＜Q B．P＝Q C．P＞Q D．不确定
10．（2分）如图是按一定规律排成的三角形数阵，按图中数阵的排列规律，第10行从左至右第6个数是（　　）

A．2 B． C．5 D．
二、填空题（本大题有10小题，每小题3分，共30分）
11．（3分）若一个多边形的每个外角都为36°，则这个多边形的内角和是　 　°．
12．（3分）我市少年军校准备从甲，乙，丙三位同学中选拔一人参加全市射击比赛，他们在选拔赛中，射靶十次的平均环数是甲＝乙＝丙＝8.3，方差是S甲2＝1.5，S乙2＝2.8，S丙2＝3.2，那么根据以上提供的信息，你认为应该推荐　 　同学参加全市射击比赛．
13．（3分）一元二次方程（a﹣1）x2﹣2x+1＝0有实数根，则a的取值范围是　 　
14．（3分）某超市一月份的营业额为200万元，一月、二月、三月的营业额共1 000万元，如果平均每月的增长率为x，则根据题意列出的方程应为　 　．
15．（3分）如图，是一个长为30 m，宽为20 m的矩形花园，现要在花园中修建等宽的小道，剩余的地方种植花草．如图所示，要使种植花草的面积为532 m2，那么小道进出口的宽度应为　 　m．

16．（3分）已知在数轴上的位置如图所示，化简：++＝　 　．

17．（3分）如图，正三角形和矩形具有一条公共边，矩形内有一个正方形，其四个顶点都在矩形的边上，正三角形和正方形的面积分别是2和2，则图中阴影部分的面积是　 　．

18．（3分）如图所示，在△ABC中，∠B＝90°，点P从A点开始沿AB边向B点以1 cm/s的速度移动，点Q从点B开始沿BC边向边C点以2 cm/s的速度移动，若P、Q分别从A，B点同时出发，则经过　 　秒，△PBQ的面积等于8 cm2．

19．（3分）如果m，n是两个不相等的实数，且满足m2﹣m＝3，n2﹣n＝3，那么代数式2n2﹣mn+2m+2021＝　 　．
20．（3分）已知图②是由图①七巧板拼成的数字“0”，若正方形ABCD的边长为12，则六边形EFGHMN的周长为 　 　．

三、解答题（本大题有7小题，共50分，解答需写出必要的文字说明、演算步骤或过程）
21．（6分）化简：
（1）．
（2）．
22．（6分）解方程：
（1）x2﹣6x﹣9＝0；
（2）9（2x+3）2＝16（1﹣3x）2．
23．（6分）如图，A、B两地之间有一座山，汽车原来从A地到B地经过C地沿折线A→C→B行驶，现开通隧道后，汽车直接沿直线AB行驶．已知AC＝10 km，∠A＝30°，∠B＝45°．则隧道开通后，汽车从A地到B地比原来少走多少千米？（结果保留根号）

24．（7分）为了倡导“节约用水，从我做起”，市政府决定对某小区500户家庭的用水情况作一次调查，市政府调查小组随机抽查了其中100户家庭一年的月平均用水量（单位：吨）．并将调查结果制成了如图所示的条形统计图．
①请将条形统计图补充完整；
②求这100个样本数据的平均数，众数和中位数．
③根据样本数据，估计该小区500户家庭中月平均用水量超过12吨的约有多少户？

25．（8分）如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12 m的住房墙，另外三边用25 m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1 m宽的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80 m2？

26．（8分）某批发商以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件，第二个月如果单价不变，预计仍可以售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降10元，可多售出100件，但最低单价应高于购进的价格；第二月结束后．批发商核对剩余的T恤一次性清仓销售，清仓时单价为40元，设第二个月单价降低x元．
（1）填表（不需化简）：
时间
第一个月
第二个月
清仓时
单价（元）
80
　 　
40
销售量
200
　 　
　 　
（2）如果批发商希望通过销售这批T恤获利8 750元，那么第二个月的单价应该是多少？
（3）如果批发商希望通过销售这批T恤获利最大，那么最大利润可达到多少元？（直接写出答案）
27．（9分）如图，四边形ACDE是证明勾股定理时用到的一个图形，a，b，c是Rt△ABC和Rt△BED边长，易知AE＝c，这时我们把关于x的形如ax2+cx+b＝0的一元二次方程称为“勾系一元二次方程”．请解决下列问题：
（1）写出一个“勾系一元二次方程”；
（2）求证：关于x的“勾系一元二次方程”ax2+cx+b＝0必有实数根；
（3）若x＝﹣1是“勾系一元二次方程”ax2+cx+b＝0的一个根，且四边形ACDE的周长是12，求△ABC面积．

参考答案
一、选择题（本大题有10小题，每小题2分，共20分）
1．【解答】解：A.是一元二次方程，故此选项符合题意；
B.由已知方程得到：x﹣3＝0，是一元一次方程，故此选项不符合题意；
C.含有两个未知数，不是一元二次方程，故此选项不符合题意；
D.含有分式，不是一元二次方程，故此选项不符合题意．
故选：A．
2．【解答】解：这组数据中数字10出现3次，次数最多，
所以这组数据的众数为10，
故选：A．
3．【解答】解：A．与不是同类二次根式，不能合并；
B．＝3，与不是同类二次根式，不能合并；
C．＝，与不是同类二次根式，不能合并；
D．＝2，与是同类二次根式，可以合并；
故选：D．
4．【解答】解：根据题意将x＝0代入方程可得：a2﹣1＝0，
解得：a＝1或a＝﹣1，
∵a﹣1≠0，即a≠1，
∴a＝﹣1，
故选：B．
5．【解答】解：A．原式＝＝13，故该选项错误，不符合题意；
B．原式＝|﹣2|＝2﹣，故该选项错误，不符合题意；
C．左边＝4，右边＝|﹣4|＝4，左边＝右边，故该项正确，符合题意；
D．原式＝＝，故该选项错误，不符合题意．
故选：C．
6．【解答】解：∵∠A+∠B+∠C+∠D＝360°，∠A+∠C＝180°，
∴∠B+∠D＝180°，
∵∠B﹣∠D＝60°，
∴2∠B＝240°，
∴∠B＝120°．
故选：C．
7．【解答】解：∵x2﹣6x+q＝0
∴x2﹣6x＝﹣q
∴x2﹣6x+9＝﹣q+9
∴（x﹣3）2＝9﹣q
据题意得p＝3，9﹣q＝7
∴p＝3，q＝2
∴x2﹣6x+q＝2是x2﹣6x+2＝2
∴x2﹣6x＝0
∴x2﹣6x+9＝9
∴（x﹣3）2＝9
即（x﹣p）2＝9
故选：B．
8．【解答】解：∵当x＝0.61时，x2+x﹣1＝﹣0.017，当x＝0.62时，x2+x﹣1＝0.004 4，
∴方程x2+x﹣1＝0一个解的取值范围为0.61＜x＜0.62，
故选：C．
9．【解答】解：∵t是方程ax2+2x+c＝0（a≠0）的一个根，
∴at2+2t+c＝0，
∴c＝﹣at2﹣2t，
∵P＝1﹣ac＝1﹣a（﹣at2﹣2t）＝a2t2+2at+1＝（at+1）2，
而Q＝（at+1）2，
∴P＝Q．
故选：B．
10．【解答】解：由图可得，
第一行1个数，
第二行2个数，
第三行3个数，
…，
则第10行10个数，
故前9行的数的个数一共有：1+2+3+…+9＝45个，
则第10行第6个数是：，
故选：D．
二、填空题（本大题有10小题，每小题3分，共30分）
11．【解答】解：∵此正多边形每一个外角都为36°，
360°÷36°＝10，
∴此正多边形的边数为10．
则这个多边形的内角和为（10﹣2）×180°＝1 440°．
故答案为：1 440．
12．【解答】解：由于1.5＜2.8＜3.2，故甲的方差最小，则甲的成绩最稳定，应推荐甲去参加比赛．
故填甲．
13．【解答】解：∵一元二次方程（a﹣1）x2﹣2x+1＝0有实数根，
∴a﹣1≠0即a≠1，且△≥0，即有Δ＝（﹣2）2﹣4（a﹣1）＝8﹣4a≥0，解得a≤2，
∴a的取值范围是a≤2且a≠1．
故答案为a≤2且a≠1．
14．【解答】解：二月份的营业额为200×（1+x），三月份的营业额在二月份营业额的基础上增加x，
为200×（1+x）×（1+x），则列出的方程是200+200（1+x）+200（1+x）2＝1 000．
15．【解答】解：设小道进出口的宽度为x m，依题意得（30﹣2x）（20﹣x）＝532，
整理，得x2﹣35x+34＝0．
解得，x1＝1，x2＝34．
∵34＞30（不合题意，舍去），
∴x＝1．
答：小道进出口的宽度应为1 m．
故答案为：1．
16．【解答】解：根据数轴得：n＞0，m＜n，m＜﹣1，
∴m﹣n＜0，m+1＜0，
∴原式＝n+n﹣m﹣（m+1）
＝n+n﹣m﹣m﹣1
＝2n﹣2m﹣1．
故答案为：2n﹣2m﹣1．
17．【解答】解：设正三角形的边长为a，则a2×＝2，
解得a＝2．
则图中阴影部分的面积＝2×﹣2＝2．
故答案是：2．

18．【解答】解：设经过x秒以后△PBQ面积为8 cm2，根据题意得
（6﹣x）×2x＝8，
整理得：x2﹣6x+8＝0，
解得：x＝2或x＝4．
答：2或4秒后△PBQ的面积等于8 cm2．
故答案为2或4．
19．【解答】解：由题意可知：m，n是两个不相等的实数，且满足m2﹣m＝3，n2﹣n＝3，
所以m，n是x2﹣x﹣3＝0的两个不相等的实数根，
则根据根与系数的关系可知：m+n＝1，mn＝﹣3，
又n2＝n+3，
则2n2﹣mn+2m+2 021
＝2（n+3）﹣mn+2m+2 021
＝2n+6﹣mn+2m+2 021
＝2（m+n）﹣mn+2 027
＝2×1﹣（﹣3）+2 027
＝2+3+2 027
＝2 032．
故答案为：2 032．
20．【解答】解：∵正方形ABCD的边长为12，
∴BD＝24，
EF＝12+6，
MH＝12+6，
∴EF＝MH＝12+6，FG＝MN＝BD＝12，NE＝HG＝BD＝6，
∴六边形EFGHMN的周长＝2（12+6+12+6）＝60+12，
故答案为：60+12．

三、解答题（本大题有7小题，共50分，解答需写出必要的文字说明、演算步骤或过程）
21．【解答】解：（1）原式＝4﹣﹣
＝4﹣；
（2）原式＝
＝．
22．【解答】解：（1）∵x2﹣6x﹣9＝0，
∴x2﹣6x＝9，
则x2﹣6x+9＝9+9，即（x﹣3）2＝18，
∴x﹣3＝，
∴x1＝3+3，x2＝3﹣3；
（2）∵9（2x+3）2＝16（1﹣3x）2，
∴3（2x+3）＝4（1﹣3x）或3（2x+3）＝﹣4（1﹣3x），
解得x1＝，x2＝．
23．【解答】解：过C作CD⊥AB于D，
在Rt△ACD中，
∵AC＝10，∠A＝30°，
∴DC＝ACsin30°＝5（km），
AD＝ACcos30°＝5（km），
在Rt△BCD中，
∵∠B＝45°，
∴BD＝CD＝5（km），BC＝5（km），
则用AC+BC﹣（AD+BD）＝10+5﹣（5+5）＝（5+5﹣5）（km）．
答：汽车从A地到B地比原来少走（5+5﹣5）km．

24．【解答】解：（1）用水11吨的户数为：100﹣20﹣10﹣20﹣10＝40（户），
将条形统计图补充完整如图所示：

（2）平均数为：（20×10+40×11+12×10+13×20+10×14）＝11.6（吨），
11出现次数最多，故众数为：11，
根据100个数据的最中间为第50和第51个数据，
按大小排列后第50，51个数据是11，故中位数为：11；
答：这100个样本数据的平均数，众数和中位数分别是11.6，11，11；
（3）500×＝150（户），
答：估计该小区500户家庭中月平均用水量超过12吨的约有150户．
25．【解答】解：设矩形猪舍垂直于住房墙一边长为x m可以得出平行于墙的一边的长为（25﹣2x+1）m，由题意得
x（25﹣2x+1）＝80，
化简，得x2﹣13x+40＝0，
解得：x1＝5，x2＝8，
当x＝5时，26﹣2x＝16＞12（舍去），当x＝8时，26﹣2x＝10＜12，
答：所围矩形猪舍的长为10 m，宽为8 m．
26．【解答】解：（1）设第二个月单价降低x元，
∵第一个月的单价为80元，
∴第二个月单价为（80﹣x）元，
∵第一个月销售量为200件，单价每降低10元，可多售出100件，
∴第二个月销售量为（200+×100）件，即（200+10x）件，
清仓时销售量为[800﹣200﹣（200+10x）]件，即（400﹣10x）件，
填表：
时间
第一个月
第二个月
清仓时
单价（元）
80
80﹣x
40
销售量
200
200+10x
400﹣10x
故答案为：80﹣x，200+10x，400﹣10x；
（2）根据题意，得
（80﹣50）×200+（80﹣x﹣50）（200+10x）+（40﹣50）（400﹣10x）＝8750，
整理，得x2﹣20x+75＝0，
解这个方程得x1＝5，x2＝15．
第二个月的单价为：80﹣5＝75（元）或80﹣15＝65（元），
答：第二个月的单价应是75元或65元；
（3）最大利润可达到9 000元理由如下：
设批发商销售这批T恤获利y元，根据题意得：
y＝（80﹣50）×200+（80﹣x﹣50）（200+10x）+（40﹣50）（400﹣10x）
＝﹣10（x﹣10）2+9000，
∵80﹣x＞50，
∴x＜30，
∵﹣10＜0，
∴抛物线开口向下，其顶点坐标（10，9 000）为最高点，
∴x＝10时，y取最大值9 000（元），
故最大利润可达9 000元．
27．【解答】（1）解：∵a，b，c是直角三角形的三边长，
∴取a＝3，b＝4，c＝5，
∴3x2+5x+4＝0是勾系一元二次方程（答案不唯一）；
（2）证明；ax2+cx+b＝0，
∵Δ＝（c）2﹣4ab
＝2c2﹣4ab，
∵a2+b2＝c2，
∴Δ＝2（a2+b2）﹣4ab＝2（a﹣b）2≥0，
∴关于x的“勾系一元二次方程”ax2+cx+b＝0必有实数根；
（3）解：∵x＝﹣1是“勾系一元二次方程”ax2+cx+b＝0的一个根，
∴，，
∵四边形ACDE的周长是，
∴2a+2b+c＝12，
∴3c＝12，
∴c＝4，
∴a2+b2＝c2＝16，，
∴（a+b）2＝32，
∴a2+2ab+b2＝32，
∴ab＝8，
∴S△ABC＝ab＝×8＝4．