物理选择性必修 第一册3 动量守恒定律同步训练题

这是一份物理选择性必修 第一册3 动量守恒定律同步训练题，共13页。试卷主要包含了单选题，综合题等内容，欢迎下载使用。

1.3动量守恒定律基础达标（含解析）
一、单选题
1.以速度 20m/s 沿水平方向飞行的手榴弹在空中爆炸，炸裂成1kg和0.5kg的两块，其中0.5kg的那块以 40m/s 的速率沿原来速度相反的方向运动，此时另一块的速率为（  ）
A. 10m/s                                B. 30m/s                                C. 50m/s                                D. 70m/s
2.质量为M的小孩站在质量为m的滑板上，小孩和滑板均处于静止状态，忽略滑板与地面间的摩擦．小孩沿水平方向跃离滑板，离开滑板时的速度大小为v，此时滑板的速度大小为（   ）
A. mMv                                 B. Mmv                                 C. mm+Mv                                 D. Mm+Mv
3.在列车编组站里，一辆质量 m1=2.7×104kg 的货车甲在平直的公路上以速度 v1 运动，碰上一辆 m2=3.6×104kg 的静止货车乙，它们碰撞后结合在以 v=1.2m/s 的速度一起继续运动。甲货车碰前的速度 v1 的大小是（   ）
A. 3.2m/s                               B. 2.8m/s                               C. 2.4m/s                               D. 3.6m/s
4.一个质量为M，长为L的小车静止在光滑水平路面上，一个质量为m的人站在小车的一端，当人从车的一端走到另一端时，小车移动的距离为（   ）
A. L                                   B. mLM-m                                   C. mLM+m                                   D. mLM
5.A、B两个物体都静止在光滑水平面上，当分别受到大小相等的水平力作用，经过相等时间，则下述说法中正确的是（    ）
A. A，B所受的冲量相同 B. A，B的动量变化相同
C. A，B的末动量相同 D. A，B的末动量大小相同
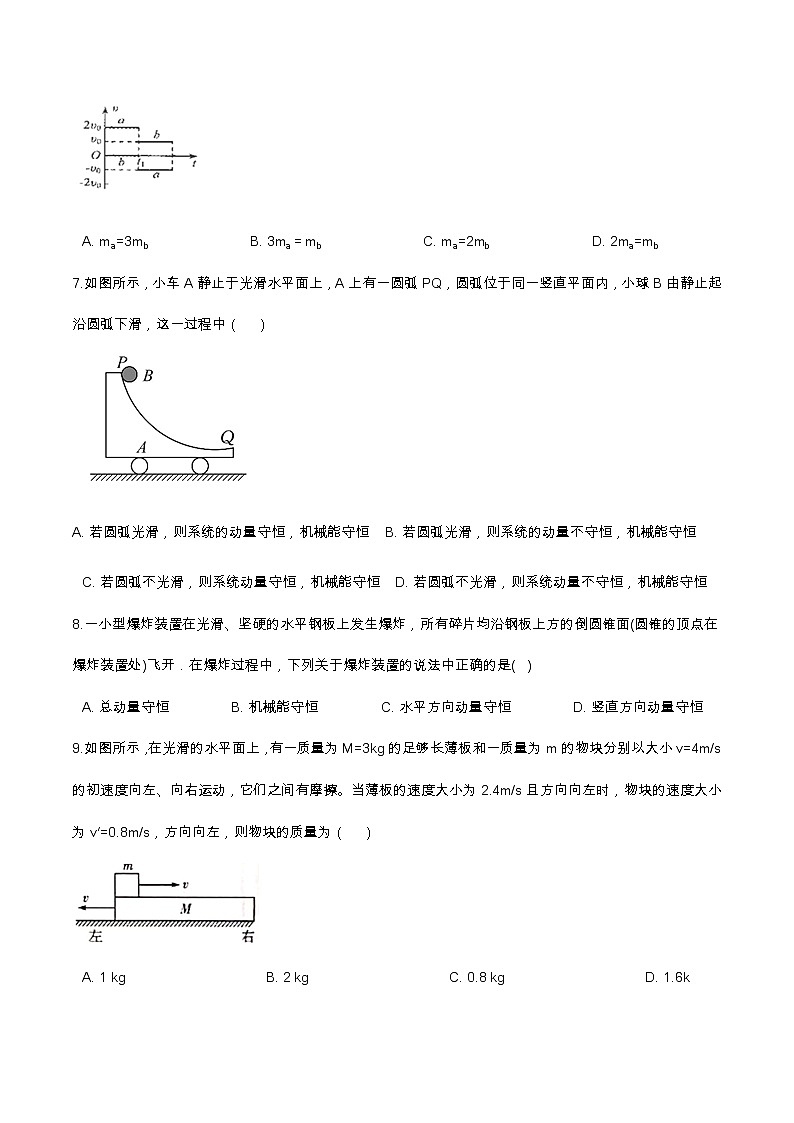
6.在光滑的水平面上有a，b两球，其质量分别是ma ， mb ， t1时刻两球发生正碰。两球碰撞前后的v—t图象如图所示。下列关系正确是（   ）

A. ma=3mb                          B. 3ma = mb                          C. ma=2mb                          D. 2ma=mb
7.如图所示，小车A静止于光滑水平面上，A上有一圆弧PQ，圆弧位于同一竖直平面内，小球B由静止起沿圆弧下滑，这一过程中（   ）

A. 若圆弧光滑，则系统的动量守恒，机械能守恒    B. 若圆弧光滑，则系统的动量不守恒，机械能守恒
C. 若圆弧不光滑，则系统动量守恒，机械能守恒    D. 若圆弧不光滑，则系统动量不守恒，机械能守恒
8.一小型爆炸装置在光滑、坚硬的水平钢板上发生爆炸，所有碎片均沿钢板上方的倒圆锥面(圆锥的顶点在爆炸装置处)飞开．在爆炸过程中，下列关于爆炸装置的说法中正确的是(   )
A. 总动量守恒                B. 机械能守恒                C. 水平方向动量守恒                D. 竖直方向动量守恒
9.如图所示，在光滑的水平面上，有一质量为M=3kg的足够长薄板和一质量为m的物块分别以大小v=4m/s的初速度向左、向右运动，它们之间有摩擦。当薄板的速度大小为2.4m/s且方向向左时，物块的速度大小为v′=0.8m/s，方向向左，则物块的质量为（   ）

A. 1 kg                                    B. 2 kg                                    C. 0.8 kg                                    D. 1.6k
10.如图所示,在光滑的水平面上有2018个完全相同的小球排成一条直线，均处于静止状态。现给第一个小球初动能Ek ， 使它正对其他小球运动。若小球间的所有碰撞都是完全非弹性的，则整个碰撞过程中因为碰撞损失的机械能总量为(   )

A. 12018 Ek                        B. 20172018 Ek                        C. 120182 Ek                        D. 20192018Ek
11.将静置在地面上，质量为M（含燃料）的火箭模型点火升空，在极短时间内以相对地面的速度v0竖直向下喷出质量为m的炽热气体．忽略喷气过程重力和空气阻力的影响，则喷气结束时火箭模型获得的速度大小是（   ）
A. mMv0                                B. Mmv0                                C. MM-mv0                                D. mM-mv0
12.如图所示，光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为mB=2mA ， 规定向右为正方向，A、B两球的动量均为6kg·m/s，运动中两球发生碰撞，碰撞后A球的动量增量为－4kg·m/s，则（    ）

A. 左方是A球，碰撞后A，B两球速度大小之比为2：5
B. 左方是A球，碰撞后A，B两球速度大小之比为1：10
C. 右方是A球，碰撞后A，B两球速度大小之比为2：5
D. 右方是A球，碰撞后A，B两球速度大小之比为1：10
13.如图所示，质量为 2m 、半径为R的大空心球B（内壁光滑）静止在光滑水平面上，有一质量为m的小球A（可视为质点）从与大球球心等高处开始无初速度下滑，滚到大球最低点时，大球移动的距离为（   ）

A. R                                          B. R2                                          C. R3                                          D. R4
14.如图所示，光滑水平面的同一直线上放有n个质量均为m的小滑块，相邻滑块间的距离为L，每个滑块均可看成质点．现给第一个滑块水平向右的初速度 v0 ，滑块间相碰后均能粘在一起，则从第一个滑块开始运动，到第n-1个滑块与第n个滑块相碰时总的时间为（　　）

A. (n2-1)L2v0                               B. n(n-1)L2v0                               C. n2L2v0                               D. n(n+1)L2v0
15.如图所示，在光滑水平面上有一质量为M的木块，木块与轻弹簧水平相连，弹簧的另一端连在竖直墙上，木块处于静止状态，一质量为m的子弹以水平速度 v0 击中木块，并嵌在其中，子弹射入木块时间极短，木块压缩弹簧后在水平面做往复运动，木块从被子弹击中前到第一次回到原来位置的过程中，木块受到的合外力的冲量大小为（　　）

A. Mmv0M+m                                  B. Mv0                                  C. 2mv0M+m                                  D. 2mv0
16.如图所示，方盒A静止在光滑的水平面，盒内有一小滑块B，盒的质量是滑块的2倍，滑块与盒内水平面间的动摩擦因数为 μ 。若滑块以速度v开始向左运动，与盒的左、右壁发生无机械能损失的碰撞，滑块在盒中来回运动多次，最终相对于盒静止，则（　　）

A. 最终盒的速度大小是 v4
B. 最终盒的速度大小是 2v3
C. 滑块相对于盒运动的路程为 v23μg
D. 滑块相对于盒运动的路程为 v2μg
二、综合题
17.算盘是我国古老的计算工具，中心带孔的相同算珠可在算盘的固定导杆上滑动，使用前算珠需要归零，如图所示，水平放置的算盘中有甲、乙两颗算珠未在归零位置，甲靠边框b，甲、乙相隔 s1=3.5×10-2m ，乙与边框a相隔 s2=2.0×10-2m ，算珠与导杆间的动摩擦因数 μ=0.1 。现用手指将甲以 0.4m/s 的初速度拨出，甲、乙碰撞后甲的速度大小为 0.1m/s ，方向不变，碰撞时间极短且不计，重力加速度g取 10m/s2 。

（1）通过计算，判断乙算珠能否滑动到边框a；
（2）求甲算珠从拨出到停下所需的时间。
18.如图，一滑雪道由 AB 和 BC 两段滑道组成，其中 AB 段倾角为 θ ， BC 段水平， AB 段和 BC 段由一小段光滑圆弧连接，一个质量为 2kg 的背包在滑道顶端A处由静止滑下，若 1s 后质量为 48kg 的滑雪者从顶端以 1.5m/s 的初速度、 3m/s2 的加速度匀加速追赶，恰好在坡底光滑圆弧的水平处追上背包并立即将其拎起，背包与滑道的动摩擦因数为 μ=112 ，重力加速度取 g=10m/s2 ， sinθ=725 ， cosθ=2425 ，忽略空气阻力及拎包过程中滑雪者与背包的重心变化，求：

（1）滑道AB段的长度；
（2）滑雪者拎起背包时这一瞬间的速度。
19.如图所示，水平地面上有一高 H=0.4m 的水平台面，台面上竖直放置倾角 θ=37° 的粗糙直轨道 AB 、水平光滑直轨道 BC 、四分之一圆周光滑细圆管道 CD 和半圆形光滑轨道 DEF ，它们平滑连接，其中管道 CD 的半径 r=0.1m 、圆心在 O1 点，轨道 DEF 的半径 R=0.2m 、圆心在 O2 点， O1 、D、 O2 和F点均处在同一水平线上。小滑块从轨道 AB 上距台面高为h的P点静止下滑，与静止在轨道 BC 上等质量的小球发生弹性碰撞，碰后小球经管道 CD 、轨道 DEF 从F点竖直向下运动，与正下方固定在直杆上的三棱柱G碰撞，碰后速度方向水平向右，大小与碰前相同，最终落在地面上Q点，已知小滑块与轨道 AB 间的动摩擦因数 μ=112 ， sin37°=0.6 ， cos37°=0.8 。
（1）若小滑块的初始高度 h=0.9m ，求小滑块到达B点时速度 v0 的大小；
（2）若小球能完成整个运动过程，求h的最小值 hmin ；
（3）若小球恰好能过最高点E，且三棱柱G的位置上下可调，求落地点Q与F点的水平距离x的最大值 xmax 。


答案解析
1.【答案】 C
【解析】手榴弹在空中爆炸过程，爆炸力远大于重力，在水平方向上动量守恒，以手榴弹原来速度为正方向，由动量守恒定律得： Mv0=m1v1+m2v2
即 1.5×20=0.5×(-40)+1×v2
解得 v2=50m/s
故答案为：C.
2.【答案】 B
【解析】设滑板的速度为 u ，小孩和滑板动量守恒得： 0=mu-Mv ，解得： u=Mmv ，B符合题意．
故答案为：B
3.【答案】 B
【解析】碰撞过程动量守恒，以甲车开始的速度方向为正方向，则 m1v1=(m1+m2)v
解得v1=2.8m/s
故答案为：B。
4.【答案】 C
【解析】设该过程人相对地面的位移为 x ，小车的对地位移为 l ，由人船模型可得 mx=Ml
又 x+l=L
联立解得小车移动的距离 l=mM+mL
故答案为：C。
5.【答案】 D
【解析】因作用力相等，作用时间相同，故力的冲量大小相同；则两物体动量的变化量相同末动量的大小一定相同；但由于不明确两动量的方向，故不能说冲量、动量变化及末动量相同；故只有D符合题意；
故答案为：D．
6.【答案】 B
【解析】由图可知b球碰前静止，设a球碰后速度为v1 ， b球速度为v2 ， 物体碰撞过程中动量守恒，规定a的初速度方向为正，有 ma⋅2v0=ma⋅(-v1)+mbv2 　①
由机械能守恒有 12ma⋅(2v0)2=12ma⋅v12+12mb⋅v22    　②
联立①②得 v1=ma-mbma+mb⋅2v0
v2=2mama+mb⋅2v0
由图可知，两球碰后速度等大反向，即 2mama+mb⋅2v0=-v0
联立得3ma=mb
故答案为：B。
7.【答案】 B
【解析】不论圆弧是否光滑，小车与小球组成的系统在小球下滑过程中系统所受合外力都不为零，则系统动量都不守恒．但系统水平方向不受外力，所以系统水平方向的动量守恒；若圆弧光滑，只有重力做功，系统的机械能守恒；若圆弧不光滑，系统要克服摩擦力做功，机械能减少，ACD不符合题意，B符合题意。
故答案为：B。
8.【答案】 C
【解析】A．爆炸装置在光滑、坚硬的水平钢板上发生爆炸，与钢板间产生巨大作用力，所以爆炸装置的总动量不守恒，A不符合题意．
B．爆炸时，化学能转化为机械能，机械能不守恒，B不符合题意．
CD．钢板对爆炸装置的作用力是竖直向上的，因此爆炸装置在竖直方向动量不守恒，而水平方向是守恒的，C符合题意，D不符合题意；
故答案为：C．
9.【答案】 A
【解析】设向左为正方向，由动量守恒定律可知： Mv-mv=Mv1+mv' ，即 3×4-4m=3×2.4+0.8m ，解得m=1kg，
故答案为：A.
10.【答案】 B
【解析】以第一个小球初速度 v0 方向的为正方向，将2018个小球组成的整体看做一个系统，设系统最终的速度为v，运用动量守恒守恒得 mv0=2018mv
解得 v=v02018
则系统损失的机械能为 ΔE=12mv02-122018mv2
解得 ΔE=20172018EK
故答案为：B。
11.【答案】 D
【解析】火箭模型在极短时间点火，设火箭模型获得速度为v，据动量守恒定律有0=（M－m）v－mv0
得 v=mM-mv0 ．
故答案为：D
12.【答案】 A
【解析】两球碰撞过程，系统不受外力，故碰撞过程系统总动量守恒；同时考虑实际情况，碰撞前后面的球速度大于前面球的速度．
规定向右为正方向，碰撞前A、B两球的动量均为 6kg⋅m/s ，说明A、B两球的速度方向向右，两球质量关系为 mB=2mA ，所以碰撞前 vA>vB ，所以左方是A球．碰撞后A球的动量增量为 -4kg⋅m/s ，所以碰撞后A球的动量是2kg•m/s，碰撞过程系统总动量守恒： mAvA+mBvB=-mAvA'+mBvB' ，所以碰撞后B球的动量是10kg•m/s，根据mB=2mA ， 所以碰撞后A、B两球速度大小之比为2：5，A符合题意．
故答案为：A
13.【答案】 C
【解析】由题意可知大球与小球在水平方向动量守恒，设小球运动到大球底部时间为t，当小球运动到大球底部时，小球在水平方向相对于大球的位移为R，设大球相对于地面的位移为x，则小球相对于地面的位移为R-x，
由动量守恒定律可知：mv1=Mv2
即：mR-xt=Mxt
解得x=R3
故答案为：C
14.【答案】 B
【解析】由于每次相碰后滑块会粘在一起，根据动量守恒定律 mv0=2mv2 ，可知第二个滑块开始运动的速度大小为 v2=12v0 ，同理第三个滑块开始滑动的速度大小为 v3=13v0 ，第n-1个球开始滑动的速度大小为 vn-1=1n-1v0 ，因此运动的总时间为 t=Lv0+L12v0+L13v0+…+L1n-1v0=Lv0(1+2+3+…+n-1)=n(n-1)L2v0 ，
故答案为：B。
15.【答案】 A
【解析】子弹击中木块过程系统内力远大于外力，系统动量守恒，设子弹与木块的共同速度为v，以向右为正方向，由动量守恒定律得mv0=（M+m）v
解得 v=mv0M+m
根据动量定理，合外力的冲量 I=Mv=Mmv0M+m
故答案为：A。
16.【答案】 C
【解析】AB．设滑块的质量为m，则盒的质量为2m，对整个过程，由动量守恒定律可得mv＝3mv共
解得v共= v3
AB不符合题意；
CD．对整个过程，由能量守恒定律可知μmgx＝ 12mv2-12×3m(v3)2
解得 x=v23μg
C符合题意，D不符合题意。
故答案为：C。
17.【答案】 （1）解：甲乙滑动时的加速度大小均为 a=μg=1m/s2
甲与乙碰前的速度v1 ， 则 v12=v02-2as1
解得v1=0.3m/s
甲乙碰撞时由动量守恒定律 mv1=mv2+mv3
解得碰后乙的速度v3=0.2m/s
然后乙做减速运动，当速度减为零时则 x=v322a=0.222×1m=0.02m=s2
可知乙恰好能滑到边框a
（2）解：甲与乙碰前运动的时间 t1=v0-v1a=0.4-0.31s=0.1s
碰后甲运动的时间
t2=v2a=0.11s=0.1s 则甲运动的总时间为 t=t1+t2=0.2s
【解析】（1）已知动摩擦因数的大小，结合牛顿第二定律可以求出甲乙运动的加速度大小，甲与乙碰前做匀减速直线运动，利用速度位移公式可以求出碰前速度的大小，甲乙碰撞过程动量守恒，利用动量守恒定律可以求出乙碰后速度的大小，结合乙做匀减速直线运动的速度位移公式可以求出运动的位移；
（2）甲碰前做匀减速直线运动，碰后做匀减速直线运动，利用速度公式可以求出碰前和碰后的运动时间。
18.【答案】 （1）设斜面长度为 L ，背包质量为 m1=2kg ，在斜面上滑行的加速度为 a1 ，由牛顿第二定律有 m1gsinθ-μm1gcosθ=m1a1
解得 a1=2m/s2
滑雪者质量为 m2=48kg ，初速度为 v0=1.5m/s ，加速度为 a2=3m/s2 ，在斜面上滑行时间为 t ，落后时间 t0=1s ，则背包的滑行时间为 t+t0 ，由运动学公式得 L=12a1(t+t0)2
L=v0t+12a2t2
联立解得 t=2s 或 t=-1s(舍去)
故可得 L=9m
（2）背包和滑雪者到达水平轨道时的速度为 v1 、 v2 ，有 v1=a1(t+t0)=6m/s
v2=v0+a2t=7.5m/s
滑雪者拎起背包的过程，系统在光滑水平面上外力为零，动量守恒，设共同速度为 v ，有 m1v1+m2v2=(m1+m2)v
解得 v=7.44m/s
【解析】（1）滑块和背包都在斜面上做加速运动，利用匀加速的位移公式结合位移相等可以求出运动的时间及滑道AB的长度；
（2）已知背包和滑雪者做匀加速直线运动，利用速度公式可以求出两者的速度大小，结合动量守恒定律可以求出滑雪者拎起背包时速度的大小。
19.【答案】 （1）小滑块在 AB 轨道上运动 mgh-μmgcosθ⋅hsinθ=12mv02
代入数据解得 v0=43gh=4m/s
（2）小滑块与小球碰撞后动量守恒，机械能守恒，
因此有 mv0=mvA+mvB ， 12mv02=12mvA2+12mvB2
解得 vA=0,vB=4m/s
小球沿 CDEF 轨道运动，在最高点可得 mg=mvEmin2R
从C点到E点由机械能守恒可得 12mvEmin2+mg(R+r)=12mvBmin2
其中 vBmin=43ghmin ，解得 hmin=0.45m
（3）设F点到G点的距离为y，小球从E点到Q点的运动，
由动能定理 12mvG2=12mvEmin2+mg(R+y)
由平抛运动可得 x=vGt ， H+r-y=12gt2
联立可得水平距离为 x=2(0.5-y)(0.3+y)
由数学知识可得当 0.5-y=0.3+y
取最小，最小值为 xmin=0.8m
【解析】（1）小滑块从斜面释放，利用动能定理可以求出滑块到达B点的速度大小；
（2）小滑块与小球碰撞的过程不受外力，利用动量守恒定律及能量守恒定律可以求出碰后速度的大小；小球恰好经过最高点，利用牛顿第二定律可以求出经过最高点的速度，再利用机械能守恒定律可以求出h的最小值；
（3）小球从E点到Q点，利用动能定理可以求出小球到达G点的速度表达式，从G点离开后做平抛运动，利用位移公式可以求出水平位移的表达式，利用数学知识可以求出水平距离的最大值。