2022年河南三门峡陕州八下期中教情学情诊断数学试题

2021-2022学年下期期中教情学情诊断

八年级数学

注意事项：

1. 本试卷共6页，三大题，23个小题，满分120分，考试时间100分钟。请用蓝黑水笔或圆珠笔直接答在试卷上。
2. 答题前请将密封线内的项目填写清楚。

一、 选择题（每小题3分，共30分 ）

1．若二次根式有意义，则x的取值范围是（   ）

A．x≥0     B．x＞0      C．x≤2    D．x＜2

2．下列二次根式中，与是同类二次根式的是（   ）

   A．      B．      C．    D．

3．下列几组数据中，能作为直角三角形三边长的是（   ）

A．2，3，4，            B．32,42,52

C．1，，             D．5,12,13

4．下列算式中，正确的是（   ）

A.          B.

C.           D.

5．已知一个直角三角形的两边长分别为3和4，则第三边长是（   ）

A.5      B.25        C.          D. 5 或

6．下列命题是真命题是（   ）

A．四边都相等的四边形是矩形

C．对角线互相垂直的平行四边形是正方形

B．菱形的对角线相等           

D．对角线相等且互相平分的四边形是矩形

7．如图所示，四边形ABCD是平行四边形，下列关系正确的是（   ）

A．AC=BD      B．    C．AB=BC    D．AB=CD

8．如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE=2，DE=6，∠EFB=60°，则矩形ABCD的面积是（   ）

A.12          B. 24         C.      D.

（第7题）          （第8题）              （第9题）

9．如图，DE是的中位线，若AD=4，AE=5，BC=12，则的周长（   ）

A．7.5        B．30         C．15       D．24

10．如图，在▱ABCD中，AB＝6，AD＝9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE于G，BG＝，则梯形AECD的周长为（   ）

A．22         B．23         C．24       D．25

二、填空题（每小题3分，共15分）

11．化简的结果是        ．

12．如果最简二次根式与可以合并，那么a=         ．

13．在实数范围内因式分解=         .

14．如图，在中，，，，则点C到AB的距离为         .

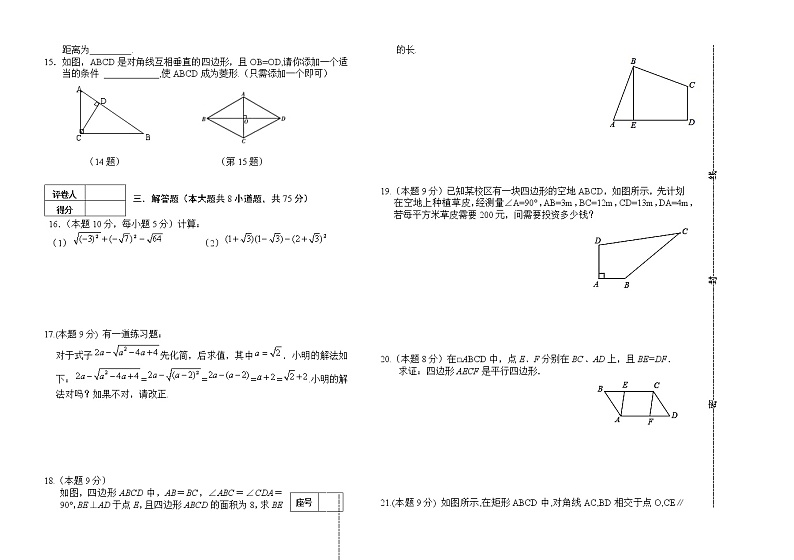
15．如图，ABCD是对角线互相垂直的四边形，且OB=OD,请你添加一个适当的条件 ____________,使ABCD成为菱形.（只需添加一个即可）

（14题）                    （第15题）

三．解答题（本大题共8小道题，共75分）

16．（本题10分，每小题5分）计算：

（1）        （2）

17.(本题9分) 有一道练习题：

对于式子先化简，后求值，其中．小明的解法如下：====.小明的解法对吗？如果不对，请改正.

18.（本题9分）

如图，四边形ABCD中，AB＝BC，∠ABC＝∠CDA＝90°，BE⊥AD于点E，且四边形ABCD的面积为8，求BE的长.  

19.（本题9分）已知某校区有一块四边形的空地ABCD，如图所示，先计划在空地上种植草皮，经测量∠A=90°，AB=3m，BC=12m，CD=13m，DA=4m，若每平方米草皮需要200元，问需要投资多少钱？

20.（本题8分）在□ABCD中，点E、F分别在BC、AD上，且BE=DF．

求证：四边形AECF是平行四边形．

21.(本题9分) 如图所示,在矩形ABCD中,对角线AC,BD相交于点O,CE∥DB,交AD的延长线于点E.试说明AC=CE．

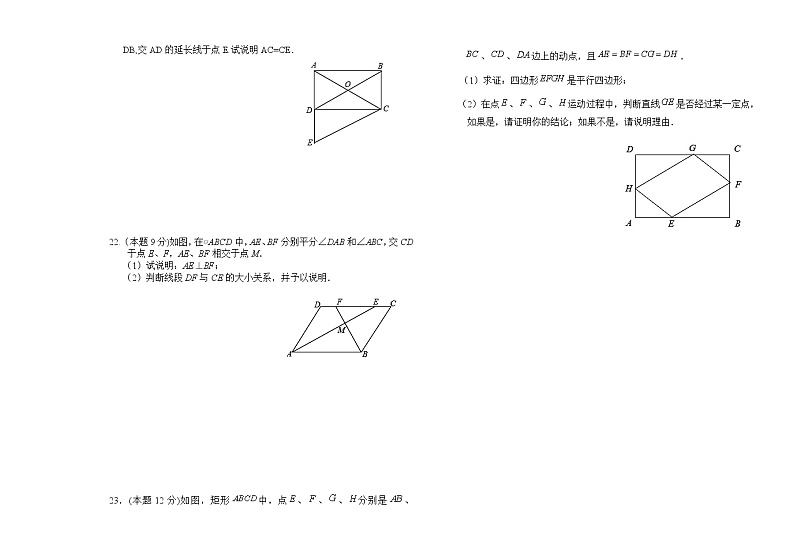
22.（本题9分)如图，在▱ABCD中，AE、BF分别平分∠DAB和∠ABC，交CD于点E、F，AE、BF相交于点M．

（1）试说明：AE⊥BF；

（2）判断线段DF与CE的大小关系，并予以说明．

23．(本题12分)如图，矩形中，点、、、分别是、、、边上的动点，且．

（1）求证：四边形是平行四边形；

（2）在点、、、运动过程中，判断直线是否经过某一定点，如果是，请证明你的结论；如果不是，请说明理由．

2021-2022下期期中答案及评分标准

八年级数学

一．          填空题（每小题3分，共30分）

1.C  2.B  3.D  4.D  5.D  6.D  7.D  8.D  9.C  10.A

二．选择题（每小题3分，共15分）

11.3  12.1   13.（X+）（X-） 14. 4.8或  15.OA=OC（不唯一）

三．解答题（共75分）

16.（每小题5分，共10分）

（1） 2        (2) -9-4

17.（9分）

解：小明的解法是错误的。                    2分

当时，原式==2a-(2-a)=3a-2=3-2     9分

18.（9分）

解：延长DC，过点BF垂直于DC延长线于点F.

可证得四边形BEDF是矩形，△ABE≌△BCF,

                        5分

从而证得证得四边形BEDF是正方形，    7分

从而证得：

S四边形ABCD=S正方形BEDF=BE2=8

BE=2                 9分

19.（9分）

解：连接DB，由题意可证得△ABD与△DBC均为Rt△       5分

从而求得：

S四边形ABCD=S△ABD+S△DBC=×3×4+×12×5=36m2                           7分

36×200=7200元                         9分

20.（8分）

证明：∵□ABCD

∴BC∥AD, BC=AD                3分

∵BE=DF

∴BC-BE=AD-DF                  5分

∴CE∥AF, CE=AF

∴四边形AECF是平行四边形                  8分

21.（9分）

证明：∵四边形ABCD是矩形

∴AD∥BC（即AE∥BC）, AC=BD

∵CE∥DB

∴四边形DECB为平行四边形

∴DB=CE

∴AC=CE

22.（9分）

证明：（1）方法一：如图①，

∵在▱ABCD中，AD∥BC，

∴∠DAB+∠ABC＝180°．

∵AE、BF分别平分∠DAB和∠ABC，

∴∠DAB＝2∠BAE，∠ABC＝2∠ABF．

∴2∠BAE+2∠ABF＝180°．

即∠BAE+∠ABF＝90°．

∴∠AMB＝90°．

∴AE⊥BF．

方法二：如图②，延长BC、AE相交于点P，

∵在▱ABCD中，AD∥BC，

∴∠DAP＝∠APB．

∵AE平分∠DAB，

∴∠DAP＝∠PAB．

∴∠APB＝∠PAB．

∴AB＝BP．

∵BF平分∠ABP，

∴AP⊥BF，

即AE⊥BF．                                     5分

（2）线段DF与CE是相等关系，即DF＝CE，

∵在▱ABCD中，CD∥AB，

∴∠DEA＝∠EAB．

又∵AE平分∠DAB，

∴∠DAE＝∠EAB．

∴∠DEA＝∠DAE．

∴DE＝AD．

同理可得，CF＝BC．

又∵在▱ABCD中，AD＝BC，

∴DE＝CF．

∴DE﹣EF＝CF﹣EF．

即DF＝CE．                               9分

23.（12分）

证明：（1）∵四边形ABCD是矩形

∴∠A＝∠B＝∠C＝∠D＝900．AB＝DC, AD＝BC

∵AE＝BF=CG＝DH

∴DG＝BE, AH＝CF

∴△HDG≌△FBE, △HAE≌△FCG(SAS)．

∴HG＝FE, HE＝FG．

∴四边形EFGH是平行四边形．                   6分

（2）在点E,F,G,H运动过程中直线GE始终经过矩形ABCD对角线的交点．（证明过程合理即可）            判断出结论9分

                                        合理证明12分

一