2021-2022学年重庆市沙坪坝区七年级（下）期末数学试卷（Word解析版）

2021-2022学年重庆市沙坪坝区七年级（下）期末数学试卷

一、选择题（本大题共12小题，共48分。在每小题列出的选项中，选出符合题目的一项）

1. 下列方程是一元一次方程的是(    )

A.  B.  C.  D.

2. 下列图形中，是轴对称图形的是(    )

A.  B.  C.  D.

3. 如图所示的是一个一元一次不等式组的解集在数轴上的表示，则此不等式组的解集是(    )

A.  B.  C.  D.

4. 已知三角形两边的长分别是和，则这个三角形第三边的长可能为(    )

A.  B.  C.  D.

5. 若是关于，的方程的一组解，则的值为(    )

A.  B.  C.  D.

6. 如图，点，，，在同一直线上，≌，，，则的长为(    )

A.
B.
C.
D.

7. 解方程时，去分母正确的是(    )

A.  B.
C.  D.

8. 已知代数式与是同类项，则，的值分别是(    )

A.  B.  C.  D.

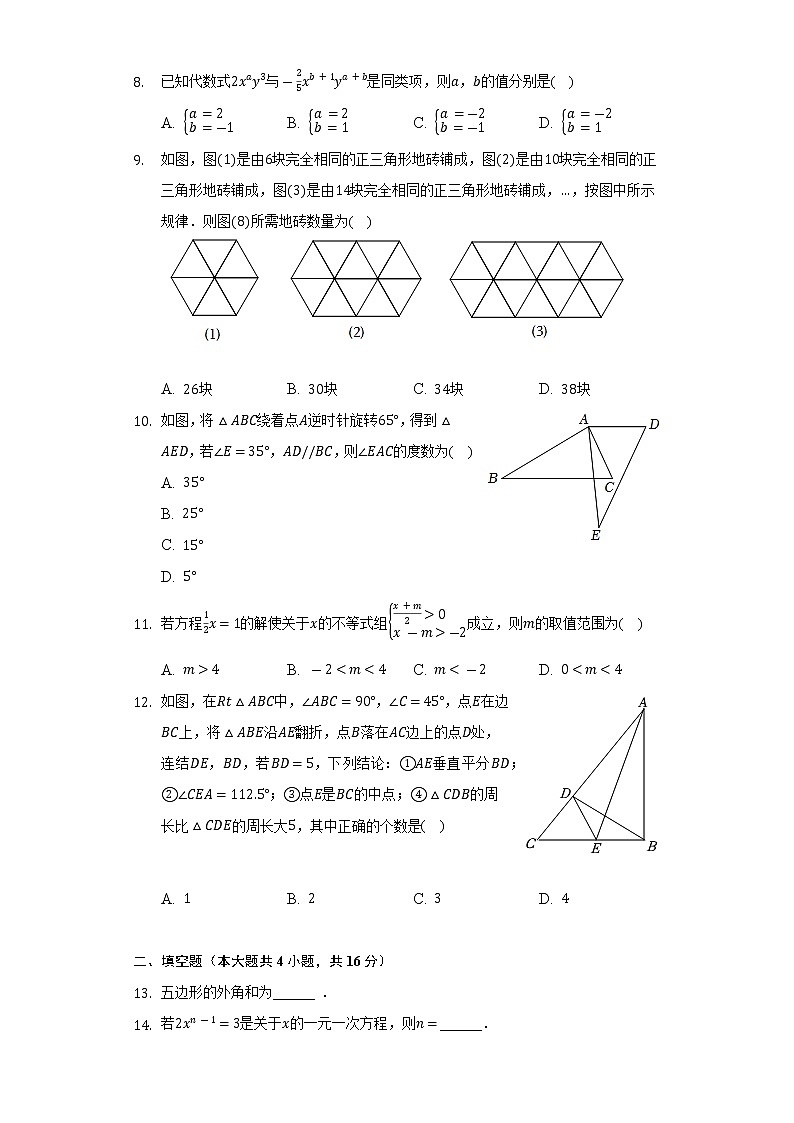
9. 如图，图是由块完全相同的正三角形地砖铺成，图是由块完全相同的正三角形地砖铺成，图是由块完全相同的正三角形地砖铺成，，按图中所示规律．则图所需地砖数量为(    )

A. 块 B. 块 C. 块 D. 块

10. 如图，将绕着点逆时针旋转，得到，若，，则的度数为(    )

A.
B.
C.
D.

11. 若方程的解使关于的不等式组成立，则的取值范围为(    )

A.  B.  C.  D.

12. 如图，在中，，，点在边上，将沿翻折，点落在边上的点处，连结，，若，下列结论：垂直平分；；点是的中点；的周长比的周长大，其中正确的个数是(    )

A.  B.  C.  D.

二、填空题（本大题共4小题，共16分）

13. 五边形的外角和为______ ．
14. 若是关于的一元一次方程，则______．
15. 已知关于的不等式组无解，且关于的一元一次方程的解满足，则所有满足条件的整数的值之和为______．
16. 随着夏天的到来，西瓜越来越受大家欢迎，月某水果店购进一批西瓜，第一周销售麒麟瓜的利润率是，销售爆炸瓜的利润率是，麒麟瓜销量是爆炸瓜销量的倍，结果第一周这两种西瓜的总利润率是，受本地西瓜的冲击，第四周销售麒麟瓜的利润率比第三周下降了，销售爆炸瓜的利润率比第一周下降了，结果第四周这两种西瓜的总利润率达到，则第四周麒麟瓜、爆炸瓜的销售之比是______利润率

三、解答题（本大题共9小题，共86分。解答应写出文字说明，证明过程或演算步骤）

17. 解下列方程组：
    ；
    ．
18. 解下列不等式组
    ；
    ．
19. 如图，在边长为个单位长度的小正方形组成的网格中，按要求作图并填空．
    将四边形向右平移个单位长度，得到四边形；
    作四边形关于点成中心对称的四边形；
    的面积为______．

20. 已知关于，的方程组的解满足，求的值及方程组的解．
21. 冰墩墩是年北京冬季奥运会的吉祥物，体现了冬季冰雪运动和现代科技特点，某班购进了一批冰墩墩吉祥物分配给班级同学，若每人分个，则剩余个；若每人分个，则还缺个，求班级中有多少名同学．
22. 如图，在中，，点是边上一点，且满足，平分交于点．
    若，求的度数；
    过点作，交于点，请说明．

23. 随着旅游业的多元化发展，自驾游呈现蓬勃发展的态势，相距千米的，两家人相约开车自驾游，若两车同时出发相向而行，先汇合后再一同前往旅游地，则出发分钟相遇；若两车同时出发同向而行，沿同一线路前往旅游地，则出发小时车可追上车．
    求，两车的平均速度分别为多少千米时；
    两家人决定同时出发同向而行，沿同一线路前往旅游地，车要想在出发后小时内追上车，求车的平均速度要在原速上至少提高多少千米时？
24. 阅读材料：一个四位自然数的千位为，百位为，十位为，个位为，若关于的一元一次方程的解为，则称这个四位自然数为方程的“顺承数”如：方程的解是，所以就是方程的“顺承数”．
    判断，是否为某个方程的“顺承数”，说明理由；
    方程的解是且，，为整数，若是该方程的“顺承数”，交换的百位和个位数字得到新数，且能被整除，求满足条件的所有的值．
25. 如图，在中，点，是边上两点，点是边上一点，将沿折叠得到，交于点，将沿折叠得到．
    如图，当点与点重合时，请说明；
    当点落在外，且，：：．
    如图，请说明；
    如图，若，将绕点顺时针方向旋转一个角度，则在这个旋转过程中，当的其中一边与的某一边平行时，直接写出旋转角的度数．
     

答案和解析

1.【答案】 

【解析】解：、未知数的最高次数是，不是一元一次方程，故本选项不符合题意；
B、含有两个未知数，不是一元一次方程，故本选项不符合题意；
C、方程左边是分式，不是一元一次方程，故本选项不符合题意；
D、符合一元一次方程的定义，故本选项符合题意．
故选：．
根据一元一次方程的定义判断即可．只含有一个未知数元，且未知数的次数是，这样的整式方程叫一元一次方程．
本题考查了一元一次方程的定义，能熟记一元一次方程的定义是解此题的关键．
 

2.【答案】 

【解析】解：因为该图形不是轴对称图形，故A选项不符合题意；
B.因为该图形不是轴对称图形，故B选项不符合题意；
C.因为该图形是轴对称图形，故C选项符合题意；
D.因为该图形不是轴对称图形，故D选项不符合题意．
故选：．
根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴，这时，我们也可以说这个图形关于这条直线成轴对称．进行判定即可得出答案．
本题主要考查了轴对称图形，熟练掌握轴对称图形的性质进行求解是解决本题的关键．
 

3.【答案】 

【解析】解：由数轴知，该不等式组的解集为，
故选：．
根据不等式解集在数轴上的表示可得答案．
本题主要考查在数轴上表示不等式的解集，用数轴表示不等式的解集时，要注意“两定”：
一是定界点，一般在数轴上只标出原点和界点即可．定边界点时要注意，点是实心还是空心，若边界点含于解集为实心点，不含于解集即为空心点；
二是定方向，定方向的原则是：“小于向左，大于向右”．
 

4.【答案】 

【解析】解：设三角形第三边的长为，由题意得：，
，
只有可以，
故选：．
根据三角形的三边关系可得，再求出解集即可．
此题主要考查了三角形的三边关系，关键是掌握三角形两边之和大于第三边．三角形两边之差小于第三边．
 

5.【答案】 

【解析】解：是方程的一组解，
，
解得，
故选：．
将，值代入方程可得关于的一元一次方程，解方程即可求解．
本题主要考查二元一次方程的解，理解二元一次方程解的定义是解题的关键．
 

6.【答案】 

【解析】解：，，
，
≌，，
，
，
故选：．
根据全等三角形的性质求出，结合图形计算，得到答案．
本题考查的是全等三角形的性质，掌握全等三角形的对应边相等是解题的关键．
 

7.【答案】 

【解析】解：解方程时，去分母得：．
故选：．
方程两边同时乘去分母得到结果，即可作出判断．
此题考查了解一元一次方程，熟练掌握等式的性质是解本题的关键．
 

8.【答案】 

【解析】解：代数式与是同类项，
，
解得：；
故选：．
根据同类项的定义得到，然后解方程组即可．
本题考查了同类项：所含字母相同，并且相同字母的指数相同的项叫同类项．
 

9.【答案】 

【解析】解：图所需要的正三角形地砖数为：，
图所需要的正三角形地砖数为：，
图所需要的正三角形地砖数为：，

图所需要的正三角形地砖数为：，
图所需要的正三角形地砖数为：，
故选：．
由题意可知，第个图所需要的正三角形地砖数为：，从而可求图所需要的地砖数．
本题考查了规律型：图形的变化类，这类题型在中考中经常出现．找出第的地砖数是解题的关键．
 

10.【答案】 

【解析】解：将绕点逆时针旋转得，

，，
，
，
，
．
故选：．
由旋转的性质可得，，由三角形内角和定理可得的度数，再由平行线的性质得，最后由角的和即可求解．
本题考查了旋转的性质，三角形的内角和定理和平行线的性质，掌握旋转的性质是本题的关键．
 

11.【答案】 

【解析】解：方程，
解得：，
不等式组整理得：，
当，即时，不等式组解集为，
方程的解能使不等式组成立，
，即，
此时的范围是；
当，即时，不等式组的解集为，
方程的解能使不等式组成立，
，即，
此时的范围是，
综上所示，的范围是．
故选：．
求出方程的解，表示出不等式组的解集，根据题意确定出的范围即可．
此题考查了解一元一次不等式组，以及解一元一次方程，熟练掌握各自的解法是解本题的关键．
 

12.【答案】 

【解析】解：由翻折可知：点落在边上的点处，
，，
垂直平分，故正确；
在中，，，
，
，
，故正确；
由翻折可知：，，
，
，
，
，
，
但时，
不是的中点，故错误；
的周长，
的周长，
的周长比的周长大，故正确．
综上所述：正确的结论是，共个．
故选：．
由折叠性质可得，，，，进而可以逐一判断即可．
本题考查图形的折叠，线段垂直平分线的性质，等腰直角三角形，熟练掌握折叠的性质是解题的关键．
 

13.【答案】 

【解析】解：多边形的外角和为，
五边形的外角和为，
故答案为：．
根据多边形外角和定理求解即可．
此题考查了多边形的内角与外角，熟记多边形的外角和为是解题的关键．
 

14.【答案】 

【解析】解：因为是关于的一元一次方程，
所以，
解得．
故答案为：．
只含有一个未知数元，并且未知数的指数是次的方程叫做一元一次方程．它的一般形式是是常数且据此解答即可．
本题主要考查了一元一次方程的定义．解题的关键是明确一元一次方程的一般形式，只含有一个未知数，且未知数的指数是，一次项系数不是．
 

15.【答案】 

【解析】解：不等式组整理得：，
不等式组无解，
，即，
方程，
解得：，
代入得：，
解得：，
的范围是，即整数，，，
则所有满足条件的整数的值之和为．
故答案为：．
表示出不等式组的解集，由不等式组无解确定出的范围，再由已知方程的解满足，确定出满足题意整数的值，求出之和即可．
此题考查了解一元一次不等式组，以及解一元一次不等式，熟练掌握不等式的解法是解本题的关键．
 

16.【答案】： 

【解析】解：设麒麟瓜与爆炸瓜每千克的成本分别为，，第一周爆炸瓜销量为，则麒麟瓜销量为，依题意有：
，
整理得：，
设第四周麒麟瓜、爆炸瓜销量分别为，，依题意有：
，
，
，
，
：：．
故第四周麒麟瓜、爆炸瓜的销售之比是：．
故答案为：：．
设麒麟瓜与爆炸瓜每千克的成本分别为，，第一周爆炸瓜销量为，则麒麟瓜销量为，根据第一周这两种西瓜的总利润率是，可以得到，设第四周麒麟瓜、爆炸瓜销量分别为，，根据第四周这两种西瓜的总利润率达到，列出方程可求四周麒麟瓜、爆炸瓜的销售之比．
本题考查了应用类问题，所以成本利润问题中的应用，理清题中的数量关系，是解题的关键．
 

17.【答案】解：
去括号得，，
移项得，，
合并同类项得，，
系数化为得，；
，
得，
解得，
把代入得，，
解得，
所以方程组的解为． 

【解析】根据等式的基本性质分别去分母、去括号、移项、合并同类项，系数化为可得答案；
根据方程组中方程的特点采用加减消元法解答即可．
本题考查了一元一次方程的解法以及二元一次方程组的解法，能把二元一次方程组转化成一元一次方程是解方程组的关键．
 

18.【答案】解：去分母得：，
去括号得：，
移项得：，
合并得：，
系数化为得：；
，
由得：，
由得：，
不等式组的解集为． 

【解析】不等式去分母，去括号，移项，合并，把系数化为，求出解集；
分别求出不等式组中两不等式的解集，找出两解集的公共部分即可．
此题考查了解一元一次不等式组，以及解一元一次不等式，熟练掌握不等式的解法是解本题的关键．
 

19.【答案】 

【解析】解：如图，四边形为所作；
如图，四边形为所作；

的面积．
故答案为：．
利用网格特点和平移的性质画出、、、的对应点、、、即可；
利用网格特点和中心对称的性质画出、、、的对应点、、、即可；
根据三角形面积公式计算．
本题考查了作图旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了平移变换．
 

20.【答案】解：，
得，
，
，
解得，
原方程组化为，
得，
解得，
将代入，
得，
解得，
原方程组的解为． 

【解析】根据题意，得，再根据已知条件可得的值，根据加减消元法解二元一次方程组即可．
本题考查了二元一次方程组的解以及解二元一次方程组，熟练掌握解二元一次方程组的方法是解题的关键．
 

21.【答案】解：设班级中有名同学，根据题意可得：
，
解得：．
答：班级中有名同学． 

【解析】设班级中有名同学，根据“若每人分个，则剩余个；若每人分个，则还缺个”以及冰墩墩吉祥物总个数不变列出方程，求解即可．
此题主要考查了一元一次方程的应用，得出正确的等量关系是解题关键．
 

22.【答案】解：，，
，
，
，
，
平分，
；
设，则，
，
，
，
，
，
，
． 

【解析】首先利用三角形外角的性质求得，再利用三角形内角和求出的度数，从而得出答案；
设，则，利用平行线的性质和三角形内角和定理分别表示出和，从而解决问题．
本题主要考查了等腰三角形的性质，三角形内角和定理，平行线的性质等知识，利用参数分别表示出和，是解题的关键．
 

23.【答案】解：可设车的平均速度为千米时，车的平均速度为千米时，依题意有：
，
解得．
故A车的平均速度为千米时，车的平均速度为千米时；
设车的平均速度要在原速上提高千米时，依题意有：
，
解得．
故A车的平均速度要在原速上至少提高千米时． 

【解析】可设车的平均速度为千米时，车的平均速度为千米时，根据若两车同时出发相向而行，先汇合后再一同前往旅游地，则出发分钟相遇；若两车同时出发同向而行，沿同一线路前往旅游地，则出发小时车可追上车；列出方程组求解即可；
设车的平均速度要在原速上提高千米时，根据两家人决定同时出发同向而行，沿同一线路前往旅游地，车要想在出发后小时内追上车，列出不等式求解即可．
本题考查一元一次不等式的应用，二元一次方程组的应用，一元一次方程的应用、路程、速度、时间的关系等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
 

24.【答案】解：是“顺承数”，
理由：是方程，
是“顺承数”；

方程的解是且，，为整数，若是该方程的“顺承数”，
四位数是：，，，，，，，，
四位数是：，，，，，，，，
能被整除，
四位数是：，； 

【解析】根据题目中给出的新定义即可求出答案；
根据的值可能是，，，，，判断出四位数，再根据能被整除，可得结论．
本题主要考查了一元一次方程的解，正确理解题目中给出的新概念是解题的关键．
 

25.【答案】证明：如图中，

由翻折变换的性质可知，，，
，，
；

证明：如图中，

：：，
可以假设，，
，
，
，，
，
，
；

解：由题意，，
，
，
，
，
，
，
如图中，当时，旋转角．

如图中，当时，旋转角．

如图中，当时，旋转角．

如图中，当时，旋转角，

综上所述，满足条件的旋转角为或或或． 

【解析】利用翻折变换的性质以及三角形内角和定理证明即可；
由：：，可以假设，，证明即可；
分四种情形：如图中，当时．如图中，当时．如图中，当时．如图中，当时，分别求解即可．
本题考查翻折变换，旋转变换，平行线的性质，三角形内角和定理等知识，解题的关键是学会用分类讨论的思想思考问题．