华师大版九年级上册1. 成比例线段导学案

教学目标

1.从生活中形状相同的图形的实例中认识相似图形.

2.了解成比例线段，比例的基本性质.

3.能根据比例的基本性质解决相关问题.

教学重难点

重点：成比例线段的定义；比例的基本性质及直接运用.

难点：比例的基本性质的灵活运用，探索比例的其他性质.

教学过程

导入新课

【问题1】

活动1（学生交流，教师点评）

教师：下面图形有什么相同和不同的地方？

学生：相同点：形状相同.

不同点：大小不相同.

教师总结：

引出课题：第23章　图形的相似

23.1　成比例线段　1　成比例线段

探究新知

探究点一　相似图形的概念

我们把具有相同形状的图形称为相似图形.

【注意】相似图形的大小不一定相同.

　　例1　下列四组图形中，不是相似图形的是（　 ）

　　　      　A　　　　　　　　　　 B       　　

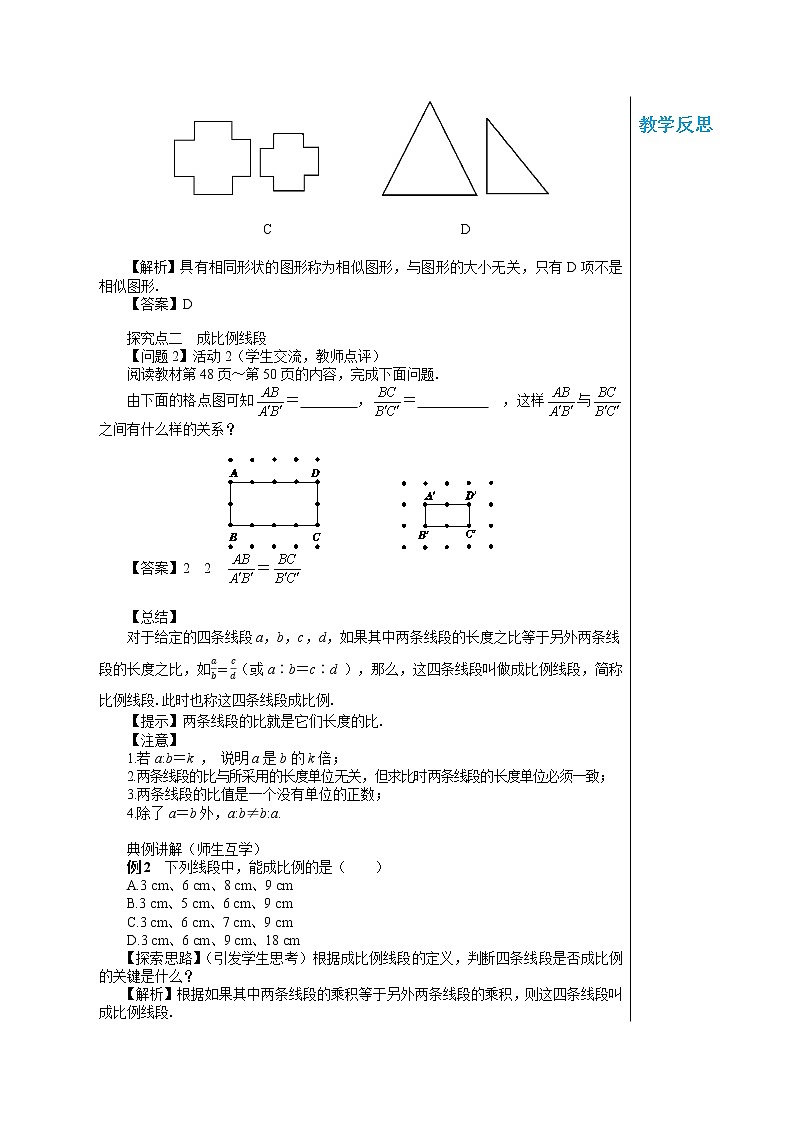
　　　　       　C                     　    D

【解析】具有相同形状的图形称为相似图形，与图形的大小无关，只有D项不是相似图形.

【答案】D

探究点二　成比例线段

【问题2】活动2（学生交流，教师点评）

阅读教材第48页～第50页的内容，完成下面问题.

由下面的格点图可知＝　　　　，＝　　　　　　，这样与之间有什么样的关系？

【答案】2　2　＝

【总结】

对于给定的四条线段a，b，c，d，如果其中两条线段的长度之比等于另外两条线段的长度之比，如（或a∶b＝c∶d ），那么，这四条线段叫做成比例线段，简称比例线段.此时也称这四条线段成比例.

【提示】两条线段的比就是它们长度的比.

【注意】

1.若a:b＝k ， 说明a是b的k倍；

2.两条线段的比与所采用的长度单位无关，但求比时两条线段的长度单位必须一致；

3.两条线段的比值是一个没有单位的正数；

4.除了a＝b外，a:b≠b:a.           

典例讲解（师生互学）

例2　下列线段中，能成比例的是（　　）

A.3 cm、6 cm、8 cm、9 cm

B.3 cm、5 cm、6 cm、9 cm

C.3 cm、6 cm、7 cm、9 cm

D.3 cm、6 cm、9 cm、18 cm

【探索思路】（引发学生思考）根据成比例线段的定义，判断四条线段是否成比例的关键是什么？

【解析】根据如果其中两条线段的乘积等于另外两条线段的乘积，则这四条线段叫成比例线段.

所给选项中，只有D项符合，3×18＝6×9.

【答案】D

【题后总结】（学生总结，老师点评）如果其中两条线段的乘积等于另外两条线段的乘积，那么这四条线段就是成比例线段.

【即学即练】

巩固练习（学生独学）

1.已知线段a＝0.3 m，b＝60 cm，c＝12 dm.

（1）求线段a与线段b的比；

（2）如果线段a、b、c、d成比例，求线段d的长.

【解】（1）∵ a＝0.3 m＝30 cm，b＝60 cm，∴ a∶b＝30∶60＝1∶2.　

（2）∵ 线段a、b、c、d是成比例线段，∴ ＝ .

∵ c＝12 dm＝120 cm，∴ ＝，∴ d＝240 cm.

【题后总结】（学生总结，老师点评）

两条线段的比与所采用的长度单位无关，但求比时两条线段的长度单位必须一致； 两条线段的比值是一个没有单位的正数.

 探究点三　比例的基本性质

【问题3】活动3（学生交流，教师点评）

用a、b、c、d表示四个数，上述四个数成比例可写成怎样的形式？

【总结】如果，那么ad＝bc；

如果ad＝bc，那么.

以上结论称为比例的基本性质.

其中a、b、c、d 叫做组成比例的项，

a、d叫做比例的外项，b、c叫做比例的内项.

特殊情况：若作为比例内项的两条线段相等，即a∶b＝b∶c，

则b叫做a、c的比例中项.

【即学即练】

2.已知：线段a，b，c满足关系式，且b＝4，那么ac＝______.

【答案】16

典例讲解（师生互学）

例3　如果，那么分别等于多少？

【解】∵ ，∴ ，

，∴ .

【拓展】比例的性质

如果，那么；

如果，那么；

如果＝…＝，那么（b+d+…+m≠0）.

拓展延伸（学生独学）

例4　已知a、b、c是△ABC的三边，且满足 ＝＝，且a+b+c＝12，请你探索△ABC的形状.

【探索思路】分析法：要判断△ABC的形状→需要知道△ABC的边长或者角度→利用两个已知等式确定 a、b、c的数量关系→得△ABC的形状.

【解】设 ＝＝＝k，可得a＝3k-4，b＝2k-3，c＝4k-8，代入a+b+c＝12，得9k-15＝12，解得k＝3.∴ a＝5，b＝3，c＝4，∴ b2+c2＝a2，即△ABC为直角三角形.

【题后总结】（学生总结，老师点评）当出现等比的条件时，可以设等比为一个常数k，从而使问题变得简单.

课堂练习

1.下列选项中与左图中的图形状相同的是（　　 ） 

A              B             C             D

2.下列各组数中一定成比例的是（        ）

A.2，3，4，5            B.-1，2，-2，4

C.-2，1，2，0           D.a，2b，c，2d

3

4.判断下列线段a、b、c、d是不是成比例线段：

（1）a＝4，b＝6，c＝5，d＝10；

（2）a＝2，b＝，c＝＝，d＝.

5.如图所示，四边形ABCD与四边形ABFE都是矩形，AB＝3，AD＝6.5，BF＝2.

（1）求下列各线段的比： 、、；

（2）指出AB、BC、CF、CD、EF、FB这六条线段中的成比例线段（写一组即可）.

参考答案

1.D　【解析】细心观察“空心圆圈”所在的“小叶片”，只有D选项中的图与原图形状相同.

2.B

3. 【解】∵，∴令x＝3k，y＝4k，∴

4.【解】 （1）因为，，所以，

所以线段a、b、c、d不是成比例线段.

（2）因为， ，所以，

所以线段a、b、c、d是成比例线段.

5.【解】（1）∵ 四边形ABCD与四边形ABFE都是矩形，AB＝3，AD＝6.5，BF＝2，∴ CD＝EF＝AB＝3，BC＝AD＝6.5，CF＝BC-BF＝4.5，∴ ＝＝，＝＝，＝.

（2）成比例线段有AB、BF、CF和EF.

课堂小结

 （学生总结，老师点评）

1.图形的相似：具有相同形状的图形称为相似图形.

 【注意】相似图形的大小不一定相同.

2.成比例线段

3.比例的基本性质：

如果，那么ad＝bc；如果ad＝bc，那么，以上结论称为比例的基本性质.

【拓展】

如果，那么；如果，那么；

如果＝…＝，那么（b+d+…+m≠0）.

布置作业

教材第51页练习题第1~3题

板书设计

课题　第23章　图形的相似

23.1　成比例线段

1　成比例线段

【问题1】　　　　　　　　　　　　　　　　　

图形的相似

【问题2】　　　　　　　　　　　　　　　　例1

成比例线段　　　　　　　　　　　　　　　　例2

【问题3】

比例的基本性质　　　　　　　　　　　　　　例3

教学反思

教学反思

教学反思

教学反思

教学反思